(описание теоретического материала по дисциплине необходимого для подготовки к выполнению заданий контрольной работы 1, примеры выполнения которой приведены ниже)

Вариантная производственная задача

Рассмотрим одну из целочисленных моделей. Предельный проявлением целочисленности является использование в модели булевых переменных - единицы и нули. Логически –это соответствует выбору между «да» и «нет». Это, в свою очередь, требует заранее сформулировать те варианты производственной программы, варианты развития экономического поведения, которые и будут в  дальнейшем подвергнуты анализу и отбору. Таким образом_, содержание задачи в данном случае состоит в следующим: принять или отвергнуть варианты из их заранее известного сформированною набора. Причем целиком принять или целиком отвергнуть (частичные решения запрещены) каждый из них. Соответствуюшую модель принято называть вариантной, ибо она построена на основании заранее известныx заданных вариантов и ее содержание будет ивляться сортировка таких вариантов на эффективные, принятые в оптимальный план, и неэффективные , т.е. отвергнутые.

Введем следующие oбозначения:

i - индекс ресурсов ;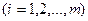

j - индекс продукции ;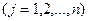

k - индекс предприятия, входящего в данное объединение, фирму ;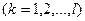

r - индекс варианта плана производства на k-м предприятии ;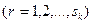

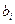 - наличный объем i-го ресурса;

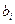 - план выпуска j-ой продукции;

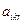 - общий объем потребления i-го ресурса на k-м предприятии при его работе целиком по r-му варианту;

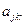 - общие размеры выпуска j-й продукции на k-м предприятии при его работе целиком по r-му варианту;

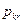 - общее количество прибыли k-го предприятия при его работе целиком по r-му варианту;

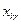 - булевая переменная принятая или не принятая.

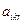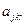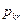Таким образом, набор известных величин ,  и  однозначно определит любой из вариантов на каждом предприятии. Следует, подчеркнуть, что в отличие от предыдущих моделей, величины 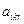,  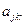и 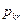 не являются удельными величинами. Они характеризуют расход ресурсов, выпуск продукции и прибыль при реализации на k-м предприятии r-го варианта в полном его объеме. Кроме того, сразу оговорим, что критерием оптимальности может быть не обязательно максимум прибыли, а любой из рассмотренных выше.

В принятых обозначениях модель вариантной производственной задачи запишется следующим образом.

Найти значения переменных. 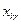 максимизирующих целевую функцию вида

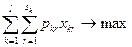                                  (2.1)

(т.е. максимизировать совокупный объем прибыли всего объединения, фирмы) при выполнении ограничений на использование ресурсов

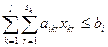
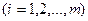;                             (2.2)

по выполнению производственной программы

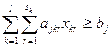
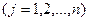;                            (2.3)

по выбору вариантов

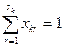
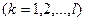;                                      (2.4)

и целочисленности переменных

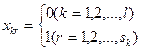.                                         (2.5)

Ограничения вида (2.5) показывает, что интенсивность использования любого из вариантов может принимать лишь два значения соответственно которым он может быть либо принят (в случае 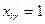), либо отвергнуть (в случае 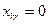). Ограничения вида (2.4) обеспечиваю на каждом предприятии выбор только одного из всех возможных на нем вариантов. Левая часть должна представлять собой сумму одной единицы: и нулей, иначе равенство в (2.4) нарушится. Таким образом, на одном предприятии нельзя выбрать как cpaзу несколько вариантов, так и ни иного. В левой части ограничений (2.2) и (2.3) каждое предприятие фактически будет представлено не суммарным по всем вариантам использованием ресурсов и выпуском продукции, а лишь теми показателями, которые описывание использование ресурсов и выпуск продукции по выбранному варианту работы данного предприятия. В силу (2.4) и (2.5)

;

.

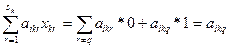
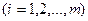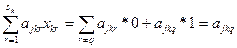
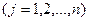где 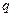 индекс того варианта работы k-го предприятия, который вошел в план (не обязательно оптимальный, но допустимый) и для которого 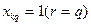. Таким oбpaзом, все прочие отвергнутые варианты как бы пропадают и не участвуют как в использовании ресурсов, так и в выпуске продукции. Аналогично и общая прибыль по объединению, фирме будет фактически формироваться включительно как сумма прибыли, oт вошедших в план вариантов.

Условие (2.4) может быть сформулировано и менее жестко, если предположить, что для каждого предприятия (в случае его меньшей выгодности по сравнению с другими) могут быть, отвергнуты все предложенные варианты. Здесь мы будем иметь случай уже не только отбора того или иного варианта на предприятии, но и отбора среди самих предприятий, сортировки их на эффективные, вошедшие в план, и неэффективные, отвергнутые. Для такой ситуации ограничения вида (2.4) будут модифицированы следующим образом:

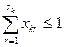
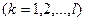                              (2.6)

Зачастую возникает и промежуточная ситуация, когда для части предприятий выбор одною из возможных вариантов обязателен. Введем обозначения:

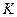 - множество индексов предприятий ;

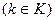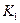 - множество индексов предприятий, участие которых в плане не обязательно, т.е. которые могут быть закрыты, перепрофилированы и т.д. ;

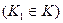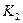 - множество индексов предприятий, участие которых в плане обязательно, т.е. не подлежащих -закрытию, перепрофилированию и т.п. .

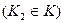С учетом этих обозначений вместо ограничений вида (2.4) в модели вариантной задачи появятся ограничения двух видов:

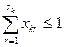
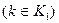;                                  (2.7)

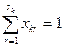
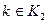.                                    (2.8)

В ограничениях вида (2.8) допускаются нулевые значения всех 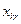,а следовательно, и нулевые значения, левой части в целом. Это будет свидетельствовать о невыгодности ни одного из вариантов работы данного предприятия, а следовательно, и о его невыгодности в целом. Выполнение условия (2.7) как строгого неравенства может свидетельствовать либо о целесообразности закрытия, перепрофилирования соответствующего предприятия, либо о недостаточном качестве набора вариантов и необходимости нахождения для него более эффективных вариантов.

Здесь отчетливо проявляется дна из основных проблем, возникающих при выборе хозяйственных решений, а именно: проблема существования и подготовки качественной исходной информации для последующего выбора на ее основе тех или иных решений.