При моделировании транспортных связей только по перевозке готовой продукции из пунктов ее производства в пункты. потребления имеем так называемую одноэтапнуро модель. При отсутствии прямых связей по поставкам продукции, наличие перевалки, длительного хранения и т п. может возникнут необходимость в применении многоэтапной модели.
Введем следующую систему обозначений:
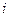 - индекс поставщика
- индекс поставщика 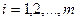 ;
;
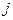 - индекс потребителя
- индекс потребителя 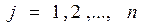 ;
;
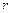 - индекс склада
- индекс склада 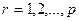 ;
;
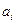 - мощность i-го поставщика;
- мощность i-го поставщика;
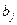 - потребность j-го потребителя;
- потребность j-го потребителя;
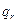 - емкость r-го склада;
- емкость r-го склада;
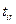 - затраты на перевозку единицы продукта от i-го поставщика на r-й склад;
- затраты на перевозку единицы продукта от i-го поставщика на r-й склад;
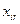 - объем перевозок от i-го поставщика на r-й склад;
- объем перевозок от i-го поставщика на r-й склад;
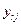 - об’їм перевозом с r-го склада к j-му потребителю;
- об’їм перевозом с r-го склада к j-му потребителю;
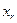 - недоиспользованная емкость r-го склада.
- недоиспользованная емкость r-го склада.
Если 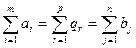 , то задачу можно решить в два этапа, т. е. сначала построить ранспортную задачу на минимуму затрат по перевозке грузов от поставщиков на склады, а затем – на минимум затрат по перевозке со складов потребителей.
, то задачу можно решить в два этапа, т. е. сначала построить ранспортную задачу на минимуму затрат по перевозке грузов от поставщиков на склады, а затем – на минимум затрат по перевозке со складов потребителей.
Если суммарная емкость складов превышают суммарные мощности поставщиков 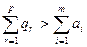 и превышают суммарные потребности потребителей
и превышают суммарные потребности потребителей 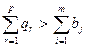 , то задачу нельзя решить в два этапа. Необходимо совместить расчет, так как в зависимости от использования емкости складов будут складываться разные схемы перевозок груза.
, то задачу нельзя решить в два этапа. Необходимо совместить расчет, так как в зависимости от использования емкости складов будут складываться разные схемы перевозок груза.
Модель многоэтапной транспортной задачи будет выглядеть следующим образом.
Критерий оптимальности – минимум суммарных транспортных затрат на перевозку грузов от поставщиков на склады и со склада потребителям
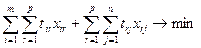 (3.1)
(3.1)
Ограничения:
- по вывозу продукции каждого поставщика
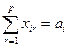
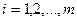 ; (3.2)
; (3.2)
- по использованию емкости каждого склада
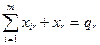
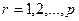 ; (3.3)
; (3.3)
- по вывозу продукции потребителям с каждого склада
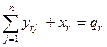
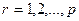 ; (3.4)
; (3.4)
- по удовлетворению потребностей каждого потребителя
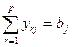
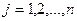 ; (3.5)
; (3.5)
- запрет на обратные перевозки
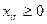
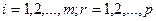 ; (3.6)
; (3.6)
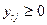
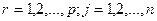 ; (3.7)
; (3.7)
- ограничение на недоиспользование емкости складов
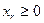
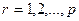 . (3.8)
. (3.8)
Рассмотрим пример многоэтапной транспортной задачи. Исходная информация представлена в таблицах 3.1-3.2.
Таблица 3.1
| Поставщики и их мощности | Склады и их емкость | ||||
| 1 | 2 | 3 | |||
|
| 550 | 550 | 550 | ||
| А | 400 | 1 | 2 | 3 | |
| Б | 600 | 6 | 4 | 3 | |
Таблица 3.2
| Склады и их мощности | Потребители и их потребности | ||||
| I | II | III | IV | ||
| 200 | 300 | 150 | 350 | ||
| 1 | 550 | 5 | 3 | 1 | 3 |
| 2 | 550 | 1 | 2 | 3 | 4 |
| 3 | 550 | 8 | 7 | 6 | 5 |
Матрица многоэтапной транспортной задачи будет выглядеть следующим образом (см. таблицу 3.3).
Таблица 3.3
| Поставщики и склады | Мощности и емкости | Склады и потребители, Емкости и потребности | ||||||
| 1 | 2 | 3 | I | II | III | IV | ||
| 550 | 550 | 550 | 200 | 300 | 150 | 350 | ||
| А | 400 | 1 | 2 | 3 | x | x | x | x |
| Б | 600 | 5 | 4 | 3 | x | x | x | X |
| 1 | 550 | 0 | x | x | 5 | 3 | 1 | 3 |
| 2 | 550 | x | 0 | x | 1 | 2 | 3 | 4 |
| 3 | 550 | x | x | o | 8 | 7 | 6 | 5 |
Матрица состоит из четырех блоков.
В левом верхнем блоке отражаются связи поставщиков со складами. Здесь указывается реальные показатели транспортных затрат.
В правом верхнем блоке описывается связи поставщиков с потребителями. Поскольку прямые оставки от поставщиков к потребителям запрещены, все показатели транспортных затрат обозначены «х» (запретительный тариф).
В левом нижнем блоке отражаются связи складов со складами. Поскольку по условию задачи перевозки грузов со склада на склад не допускаються, во всех клетках того блока (за исключением главной диагонали) проставлен запретительный тариф (х). Каждая клетка главной диагонали описывает связь конкретного склада с самим собой. В таких клетках транспортные затраты принимаются равными нулю Если в результате решения задачи клетка главной диагонали оказывается заполненной, то число в ней будет показывать недоиспользованную емкость склада. Главная диагональ левого нижнего блока называется фиктивной диагональю, соответственно и метод решения многоэтапной транспортной задачи называется методом фиктивной диагонали.
В правом нижнем блоке описываются связи складов с потребителями. Указываются реальные затраты на транспортировку.
До сих пор мы рассматривали транспортные задачи в матричной форме. Каждое пересечение строки и столбца этой матрицы соответствует транспортному маршруту, связывающему данную пару пунктов «поставщик-потребитель». Реально на транспортной сети таких маршрутов может быть несколько. Поэтому при матричной постановке необходимо заранее, до составления и решения задачи, выбрать из нескольких возможных один маршрут для каждой пары пунктов «поставщик-потребитель». Чаще такой выбор осуществляется довольно просто - по кратчайшим расстояниям, по минимуму транспортных затрат или же берутся так называемые «рациональные направления» перевозок. Реже, хотя это и более обоснованно, решаются специальные задачи по выбору маршрутов.
Необходимость в таком предварительном этапе отпадает при сетевой постановке задачи, так как транспортная сеть непосредственно моделируется в задаче с помощью аппарата теории графов. Каждая вершина графа соответствует поставщику, потребителю или транзитному пункту, каждая дуга - участку транспортной сети. Решение задачи в сетевой постановке позволяет выбрать в увязке с многими показателями и оптимальные маршруты перевозки для каждой пары «поставщик-потребитель».
Рассмотрим транспортную задачу в сетевой постановке. Введем следующую систему обозначений:
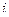 - индекс поставщика,
- индекс поставщика, 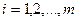 ;
;
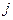 - индекс потребителя,
- индекс потребителя, 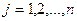 ;
;
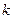 - индекс транзитного пункта,
- индекс транзитного пункта, 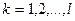 ;
;
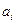 - мощность i-го поставщика;
- мощность i-го поставщика;
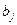 - потребность j-го потребителя;
- потребность j-го потребителя;
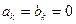 = в транзитном пункте продукция не производиться и не потребляеться;
= в транзитном пункте продукция не производиться и не потребляеться;
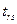 - затраты на перевозку единицы продукта между двумя соседними звеньями транспортной сети (
- затраты на перевозку единицы продукта между двумя соседними звеньями транспортной сети ( 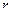 и
и 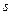 );
);
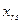 - объем перевозок между двумя соседними звеньями транспортной сети (
- объем перевозок между двумя соседними звеньями транспортной сети ( 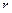 и
и 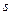 ).
).
Модель транспортной задачи в сетевой постановке будет выглядеть следующим образом.
Критерий оптимальности – минимум суммарных транспортных затрат
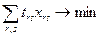 (3.9)
(3.9)
Ограничения:
- балансы распределения продукции каждого поставщика
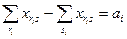
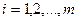 , (3.10)
, (3.10)
т.е. мощность каждого поставщика формируется как разность между тем, что в данную вершину ввозится и тем, что из нее вывозится;
- балансы удовлетворения потребностей каждого потребителя
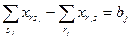
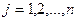 ; (3.11)
; (3.11)
- балансы продукции в каждом транзитном пункте
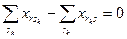
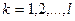 ; (2.20)
; (2.20)
- запрет на обратные перевозки
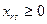 (3.12)
(3.12)
Дата: 2019-03-05, просмотров: 477.