Основными ресурсам дня добычи топлива (торфа или угля) являются электроэнергия, оборотные средства топливодобывающего предприятия и трудовые ресурсы. Все они стpoгo лимитированы. Добываемых видов топлива два - торф .(открытые разработки) и уголь (подземная добыча). В рамках выделенных объемов ресурсов план добычи может быть любой. Нас же будет интересовать прежде всего максимум теплотворной способности добытого топлива. Нормы затрат ресурсов на торф и уголь, а также лимиты ресурсов и коэффициенты перевода в условное топливо даны в таблице 1.1.
Таблица 1.1
| Вид ресурсов | Единица измерения | Количество ресурсов | Норма затрат ресурсов на добычу 1 т | |
| торф | угля | |||
| Оборотные средства | у.е. | 20000 | 00,5 | 0,5 |
| Электроэнергия | кВт*ч | 180000 | 1,1 | 1 |
| Трудовые ресурсы | чел.*ч | 32000 | 0,225 | 0,25 |
| Коэффициенты перевода торфа и угля в тонны условного топлива | 0,25 | 1,2 | ||
Неизвестными в задаче являются добыча торфа и угля (в т.). Обозначим их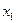 
и 
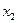соответственно. Задача ставиться следующим образом: найти неотрицательные значения переменных 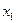и 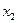, максимизируюших суммарную теплотворную способность добытого топлива при ограничениях на выделенные лимиты ресурсов. Математическая модель задачи будет выглядеть так:
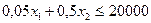; (1.1)
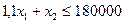; (1.2)
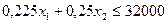; (1.3)
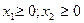; (1.4)-(1.5)
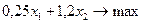(1.6)
Совокупное выражений (1.1)-(1.6) представляет собой математическую модель задачи, данные табл. 1.1 с сопровождающими ее пояснениями - экономическую модель, т,е. описание основных сторон деятельности объекта, абстрагируясь от множества второстепенных (точнее, признанных таковыми в данном случае) eго свойств.
Экономико-математическая модель - совокупность математических выражений и экономическое описание входящий в них величин. Совокупность математических выражений (1.1)-(1.6) состоит из критерия оптимальности (1.6) и системы ограничений (1.1)-(1.5). В свою очередь, в последней можно выделить ограничения неотрицательности (1.4)-(1.5), показывающие, какие значения могут принимать переменные, а также основные ограничения (1.1)- (1.3), указывающие, какие именно преобразования можно проводить с переменными. Система ограничений определяет множество допустимых значений переменных, из которых с помощью критерия оптимальности и отыскивается наилучшие (по данному критерию) значения.
Запишем экономико-математическую модель рассмотренной задачи, но уже не и конкретном, а в общем виде, т.е в символах.
Обозначим:
i - индекс ресурсов {i= 1,2,…,m);
j - индекс продукции (j= 1,2,…,n);
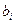- наличный объем i-ro ресурса;
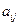- норма затрат i-го pecyрса на производство единицы j-й продукции;
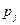- эффективность единицы продукции j-го вида;
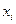- искомый объем производства j-й продукции.
В данных обозначениях задача запишется следующим образом.
Найти значения переменных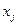 
максимизирующие целевую функцию вида
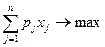(1.7)
при выполнении ограничений на использование ресурсов:
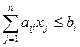
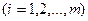(1.8)
и неотрицательности переменных:
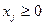
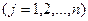(1.9)
Выражение (1.7) максимизирует совокупный эффект oт всего объема выпушенной продукции всех видов. Выражение (1.8) означает, что для любого из ресурсов его суммарный расход на производство продукции (вcex видов) не превосходит выделенного лимита. Выражение (1.9) означает неотрицательность выпусков продукции.
Модель (1.7)-(1.9) справедлива для любого количества видов ресурсов и продукции, для самых разнообразных конкретные численных значений лимитов ресурсов 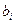, и норм затрат ресурсов 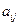. Использование более общего термина «продукция» вместо конкретного «топливо» превращает задачу по отысканию оптимального плана добычи топлива в задачу по отысканию оптимального плана производства любой продукции (в том числе, разумеется, и топлива). Соответственно этому, коэффициенты при неизвестных из критерия оптимальности (1.7). т.е. величины 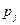, были определены выше й самом общем виде как эффективность единицы продукции
Таким образом, модель (1.7)-(1.9) соотвествует любой экономической задаче по отысканию максимума эффекта oт выпуска продукции при ограничениях, на количество используемых ресурсов. Конечно, при условии, что размеры эффекта и использования ресурсов линейно зависят от объема выпуска.
1.2. Задача на максимум дохода
Соизмерение различных видов продукции через натуральные показатели возможно лишь в ограниченном числе случаев Поэтому; в качестве критериального показателя используются, как правило, различного рода стоимостные величины, например доход.
Пусть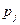 
- доход от производства единицы продукции j-го вида (удельный доходов продукции).
Тогда модель (1.7)-(1.9) есть модель задачи на максимум дохода. Оптимальное использование ресурсов в данном случае заключается в получении максимального объема дохода. Различные варианты использования ресурсов есть не что иное, как варианты плана выпуска продукции (т.е. те или иные значения неизвестных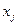 
).
Все эти варианты одинаковы по размерам используемых ресурсов (заданы величинами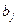 
), т.е. одинаковы по затратам, но различны по своим результатам - по размерам дохода. Отметим, что именно фиксированный уровень затрат ресурсов дает возможность отбирать наилучший вариант по максимуму результата.
В модели (1.7)-(1.9} средством оптимизации является отбор в план наиболее выгодных видов продукции. При наличии нескольких взаимозаменяемых способов (технологий) производства одного и того же вида продукции оптимизация возможна и зa счет выбора, для каждой продукции наиболее выгодных способов ее производства. Дополнительно введем следующие обозначения:
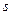- индекс технологического способа производства продукции ( 
);
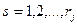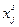- искомый объем производства j-й продукции s-м технологическим способом;
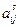- норма затрат i-го ресурса на производство единицы j-й продукции s-м способом;
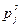прибыльноcть j-й продукции, произведенной s-м способом.
Модель запишеться так:
критерий оптимальности - максимум дохода
;
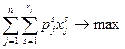ограничение на использование ресурсов
;
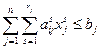
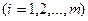ограничения на неотрицателъность выпуска
.
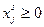
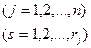Теперь в задаче на максимум дохода каждому виду продукции j соответствует не одно неизвестное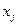 
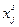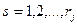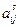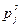, а несколько неизвестных (для всех ) по числу имеющихся технологических способов производства j-й продукции. Каждый способ задается набором показателей и Различия способов определяются различиями в величине удельного дохода и норм затрат ресурсов.
Подчеркнем, что наличие для каждого вида продукции своего набора технологий требует использования подиндекса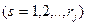 
. Напротив, использо вание более простой записи 
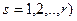будет соотвствовать наличию общего набора технологий, пригодных для производства любого вида продукции.
Интерпретируем приведенный выше числовой пример как задачу максимизации прибыли от добычи топлива одного вида (например, угля) двумя различными технологическими способами: открытым (карьер) и подземным (шахта). При практической близости норм затрат электроэнергии (1,1 и 1 кВт ч.} и трудовых ресурсов (0,225 и 0,25 чел.-ч) на добычу 1 т торфа и 1 угля два технологических способа отличаются, главным образом, величиной затрат оборотных средств (10-кратное увеличение в расчете на тонну угля при переходе к подземной добыче) и существенными различиями в прибыльности (почти 5-кратное уменьшение в расчете на тонну угля при переходе к открытой добыче). Последнее может быть объяснено, например дифференциацией цен в связи с лучшими качествами глубокозалегающих углей (меньшая зольность, низкое содержание серы и т.д.).
Следует отметить, что в экономико-математической задаче для выделения разных технологических способов производства одноименной продукции достаточно различий в величине нормы затрат лишь одного какого-либо ресурса либо - только критериального показателя. Так, например, томаты, выращенные в июле и августе по одной и той же «реальной» технологии, с одинаковыми нормами затрат ресурсов, в задаче будут представлены двумя «модельными» технологиями, отличающимися лишь величиной 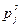- различной прибыльностью единицы продукции в июле и августа, вследствие различий сезонным цен.
В процессе составления плана производства приходится учитывать не только ограниченность выделяемых ресурсов, но и возможные директивные задания по выпуску продукции. Введен в наш первоначальный пример плановые задания по добыче 90 тыс.т торфа и 30 тыс.т угля. Модель (1.1)-(1.6) дополнится ограничениями по выпуску:
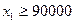; (1.10)
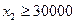. (1.11)
Выражения (1.10) и (1.11) означают, что добыча торфа и угля должна быть не меньше плановых заданий.
Следую отметить, что как здесь, так и далее термин «плановое задание или «план» нами употребляется (если это не оговорено специально) лишь для краткости и не несет однозначной смысловой нагрузки. Так, это могут быть и обязательные объемы выпуска. Например, в размере выигранного по конкурсу государственного заказа или заранее заключенных договоров с потребителями нашей продукции при рыночной системе хозяйства. Аналогично используется нами и термин «лимиты ресурсов», отнюдь не обязательно означающий их строгое лимитирование.
Введем обозначения.
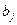- план выпуска j-й продукции. С учетом ранее введенных обозначений численной модели (1.1)-(1.6), (1.10)-(1.11) будет соответствовать модель в общем виде:
;
;
.
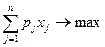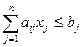
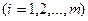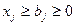
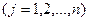Если в задаче (1.7)-(1.9) оптимизация шла за счет отбора наиболее выгодных видов продукции, то в последней модели свобода выбора существенно снижается. Действительно, в любом допустимом плане выпуска величина каждого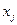 
в основном складывается из обязательной фиксированной величины планового выпуска 
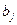. Оптимизация же, т.е. выбор различных вариантов идет лишь зa счет сверхплановых выпусков продукции того или иного вида. Пусть 
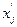- искомый сверхплановый выпуск j-й продукции. Тогда 
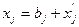. Подставим это выражение в модель:
;
.
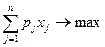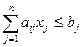
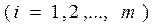
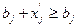
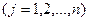Уменьшив правую и левую части последнее выражении на 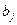, получим 
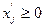- условие неотрицательности вновь введенных переменных
Общая величина дохода от планового выпуска продукции в строгом соответствии с планом постоянна и может быть получена прямым счетом. Иными словами,
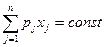
Таким образом, максимизация общего объема дохода зависит лишь от сверхпланового выпуска, т.e. величины
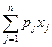
Учитывая, что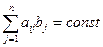 
, обозначим через 
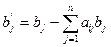остаток i-го ресурса после строгого выполнения плана. Тогда вся задача сведется к максимизации дохода от сверхпланового выпуска продукции за счет свободного остатка ресурсов. Этой задаче будет соответствовать модель:
;
;
.
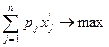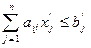
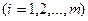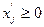
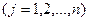По своей записи она точно повторяет первоначальную модель (1.7)-(1.9). Штрихи при символах лишь напоминают о наличии в данном случае «предмодельного», «дооптимизационного» этапа, содержанием которого является прямой счет расчетных показателей. Здесь мы видим пример того, как двум различным экономическим задачам, т.e. максимизации дохода от использования ресурсов с учетом плановых заданий по выпуску продукции или же при полной свободе выбора плана выпуска соответствуют однотипные экономико-математические задачи, решаемые по одной и той же оптимизационной модели. Таким образом, самостоятельного значения третья модель не имеет и в ее непосредственном использовании смысла нет.
Введем ограничений по формированию производственной программы; в модель, учитывающую наличие разных технологических способов производства одноименной продукции. Тогда ее запись будет выглядеть так:
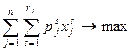; (1.12)
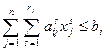
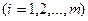; (1.13)
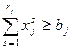
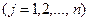; (1.14)
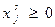
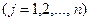
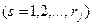. (1.15)
Условия {1-14) означает, что при всех технологических способах, используемых при производстве данной продукции, eе суммарный выпуск должен быть не менее запланированного объема. Один и тот же плановый выпуск продукции в размере 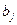, может быть получен различными сочетаниями величин 
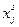, т.е. различными вариантами «технологической» структуры выпуска. В данном случае, в отличие от предыдущей постановки задачи упрощение модели невозможно. В задаче (1.12)-(1.15) оптимизируются не только сверхплановые выпуски, но и выпуски в строгом соответствии с заданиями 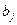за счет подбора наиболее выгодных технологий из всех возможных для производства данного вида продукции. Действительно, даже запись условия (1.14) в виде строгого равенства
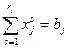
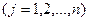
оставляет свободу выбора величины каждого из слагаемых .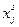
Задача на минимум затрат
Введем новое обозначение: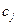 
- себестоимость единицы j-й продукции.
Запишем простую модель с критерием оптимальности - минимум затрат на весь объем выпуска:
;
.
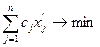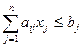
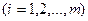
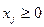
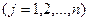Поиск оптимального решения в этом случае очень прост - им является тривиальное (все неизвестные равны нулю) решение. Действительно, при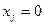 
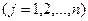все ограничении выполняются, т.е. данное решение допустима A из вcex допустимых решений оно дает наименьшее значение критерия оптимальности, т.е. затраты в данном случае равны нулю (очевидно, что отрицательными они быть не мoгyт).
Такое математически правильное решение с экономической точки зрения абсурдно, ибо представляет собой план «максимальной экономии ресурсов», в соответствии с которым ничего не производится и все ресурсы остаются целиком неиспользованными.
Ничего не изменит и запись модели, усложненная за счет введении различных технологических способов производства одноименной продукции, где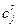 
- себестоимость единицы продукции j-гo вида, произведенной по s-му способу.
Чтобы значение критерия оптимальности не «скатывалось» до нуля, необходимо ограничит снизу (т.е. ввести ограничение вида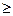 
) решение. Такими условиями, как мы уже знаем, являются условия по выполнению директивно заданного плана производства.
Экономическая деятельность, как одна из видов человеческой, целенаправленна и предполагает достижение определенных результатов производства, что, и в свою очередь, связано с осуществлением затрат. Одной из основных задач экономики (как науки, так и практики) является сопоставление затрат и результатов. Как правило, существует несколько вариантов получении заранее заданною (планируемого, желаемого, предполагаемого, фиксированного) результата. Также существует несколько вариантов использования известного (имеющегося), фиксированного количества ресурсом. Правильный выбор наилучшею варианта из нескольких допустимых возможен при следующих постановках задачи:
- максимизация результата (эффекта) при фиксированном уровне затрат (ресурсов);
- минимизация затрат при фиксированном уровне результатов.
Сам отбор наилучшего варианта решения (плана производства) по минимуму затрат возможен вследствие эквивалентности результатов по всем вариантам. В случае же различной величины результатов вариант с меньшими затратами может и не быть лучшим (просто с меньшими затратами мы достигаем и меньшего результата). Именно это имело место выше. «Лучшее», нулевое решение давало наименьший (выпуск равен нулю) результат.
Рассмотрим модель задачи на минимум затрат при фиксированных планах производства, предположив, что каждый вид продукции производится лишь одним технологическим способом:
;
.
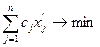
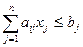
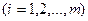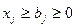
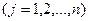Любой сверхплановый выпуск, даже самых скромных размеров, увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при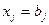 
. Тем самым данная модель теряет смысл, так как в подобной задаче нечего искать. Оптимальный план известен: он задается числами 
.
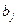Однако это не значит, что при отсутствии нескольких способов производства одноименной продукции постановка задачи на минимум затрат бессмысленна. Нужно лишь задать peзультат с меньшей, степенью подробности, нежели искомые величины:
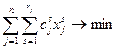; (1.16)
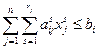
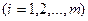; (1.17)
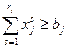
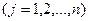; (1.18)
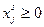
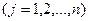
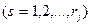(1.19)
В модели (1.16)-(1.19) переменные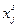 
детализированы и по видам продукции j и по способам производства s, а плановые задания 
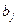- лишь по продукции. Поэтому оптимизация осуществляется подбором разных величин 
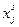в рамках единой фиксированной величины 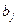, т.e. подбором сочетания различных технологий для выпуска данной j-й продукции.
Рассмотрим еще один подход, позволяющий ограничить решение в задаче на минимум затрат снизу. Обозначим в данном случае через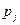 
цены на продукцию j-ro вида, а через Р - план по валовой продукции. Заменим детальные ограничения 
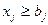aгpегированным ограничением 
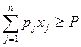(если вернутся к первоначальному определению величии 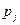, то Р будет не чем иным, как запланированным уровнем валового дохода от выпуска продукции)
Тогда модель на минимум затрат в случае, когда каждый вид продукта производится лишь одним технологическим способом, запишется так
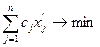; (1.20)
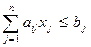
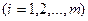; (1.21)
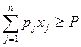; (1.22)
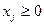
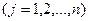. (1.23)
Отметим одну важную особенность рассмотренных моделей (1.16)-(1.19) и (1 20)-(1.23). Ограничения на область допустимых решений (1.17)-(1.18) и (1.21)-(1.22) в принципе противоречивы: ограничения вида «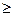 
» по объему производства или валовому доходу могут потребовать расхода одного или нескольких ресурсов, превышающего их наличный зaпаc, учитываемый в ограничениях вида « 
».
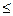Противоречивость рассматриваемых ограничений при решении задачи с конкретными значениям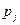и и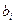 
может привести к тому, что область допустимых решений окажется пустой и оптимизационная задача будет неразрешимой.
Дата: 2019-03-05, просмотров: 228.
