Цель работы: Изучение конструкции и назначения шпинделей, проверить на прочность шарнир универсального шпинделя.
Задание: Выполнить расчет на прочность шарнир универсального шпинделя,
если известны следующие исходные данные: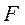 
– сила действующая
на щеку шпинделя;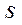 
– плече приложения силы; 
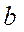– ширина щеки
шпинделя;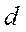 
– диаметр тела шпинделя; 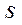– плече приложения
силы. Исходные данные приведены в таблице 7.1.
Теоретическая часть
Проверка на прочность щеки головки шпинделя. На рис.7.1 представлена схема действия сил на щеки головки шпинделя при передаче им крутящего момента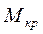 
. На каждую щеку шпинделя будет действовать сила 
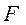, возникающая в результате давления лопасти на бронзовый вкладыш и бронзового вкладыша на щеку по цилиндрической поверхности их соприкосновения.
Момент, передаваемый шпинделем, будет равен
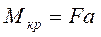; (7.1)
где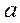 
– расстояние между точками приложения сил.
Принимаем, что удельные давление вкладыша на щеку шарнира распределяются по трапеции и сила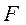 
приложена в плоскости центра тяжести этой трапеции. Обычно 
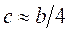и 
; 
.
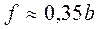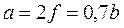Таким образом, при передаче шпинделем крутящего момента в сечении I - I на расстоянии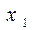 
от оси шарнира будут возникать напряжения и от кручения, и от изгиба.
Напряжение кручения в сечении I - I будет равно
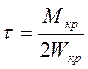; (7.2)
где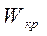 
- момент сопротивления сечения I - I кручению.
Для определения момента сопротивления кручению по заданным размерам головки шпинделя сечение I - I вычерчено отдельно в виде сегмента.
Определить точное значение момента сопротивления кручению сечения, имеющего форму сегмента, трудно, поэтому обычно сегмент приравнивают равновеликому по площади прямоугольнику высотой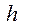 
и шириной 
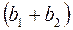. Момент сопротивления сечения прямоугольника кручению определяют по формуле
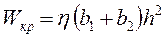; (7.3)
где коэффициент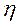 
зависит от отношения ширины прямоугольника к его высоте. При 
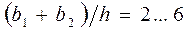величина 
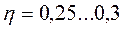. Тогда 
, 
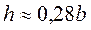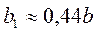и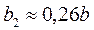 
.
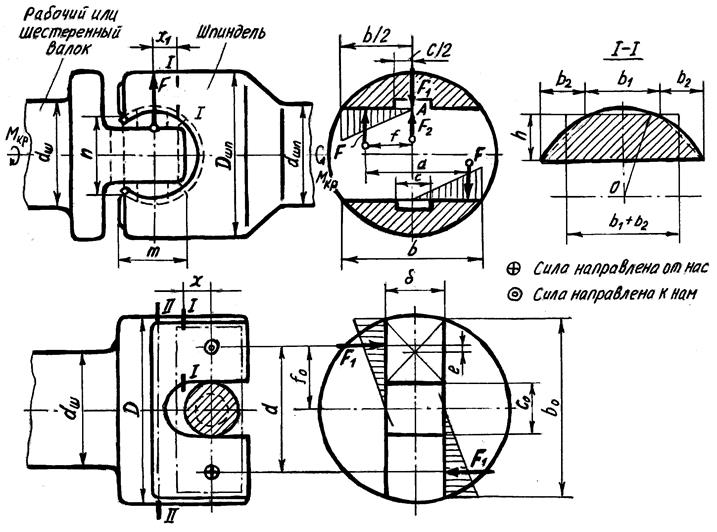
Рис.7.1. К расчету шарнира универсального шпинделя.
Напряжение изгиба в сечении щеки I - I будет равно
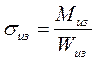; (7.4)
где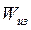 
- момент сопротивления сечения I - I изгибу.
Из рис. видно, что момент изгиба сечения I - I равен произведению силы F на плечо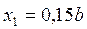 
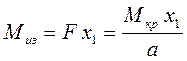. (7.5)
Определить момент сопротивления изгибу сечения I - I, имеющего форму сегмента, тоже весьма трудно, поэтому пользуются приближенной формулой. Для этого сегмент заменяем равновеликой по площади трапецией с основанием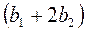 
и высотой 
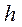. Момент сопротивления сечения трапеции изгибу равен
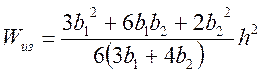. (7.6)
Расчетное напряжение в сечении щеки I - I от действия изгиба и кручения определяют по формуле
.
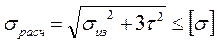Шпиндели обычно изготовляют из углеродистой кованной стали, марки 40 или из легированных сталей 40Х, 40ХН, 40ХНМ, и пр. Предел прочности этих сталей равен 750 – 950 МПа. Принимать необходимо пятикратный запас прочности.
Кроме определения напряжения в сечении I - I, необходимо так же проверить напряжение в теле шпинделя в его средней части по длине. Очевидно, что тело шпинделя работает только на кручение, и напряжение в любом сечении по длине шпинделя между его шарнирами будет равно
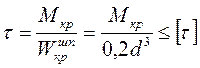; (7.7)
где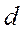 
– диаметр тела шпинделя, 
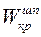- момент сопротивления кручению тела шпинделя, 
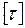- допустимое напряжение 
.
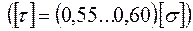Проверка на прочность лопасти валка. Так же как и при расчете щеки головки шпинделя, при расчете лопасти примем, что удельные давления от вкладыша распределяются на поверхности каждой вилки по трапеции и сила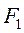 
, действующая на вилку при передаче лопастью крутящего момента 
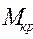равна
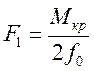; (7.8)
где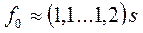 
- плечо приложения силы.
Сила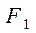 
будет приложена эксцентрично относительно центра сечения вилки толщиной 
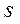. Очевидно, что эта сила будет скручивать сечение вилки моментом
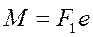; (7.9)
где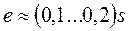 
- эксцентриситет приложения силы 
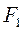относительно центра тяжести сечения вилки.
Этот момент будет скручивать сечение вилки и создавать в ней напряжения кручения. Вместе с тем сила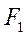 
будет создавать изгибающий момент относительно сечения I - I и в этом сечении будут возникать напряжения изгиба.
Таким образом, при передаче лопастью крутящего момента в сечении I - I вилки будут возникать и напряжения кручения, и напряжения изгиба.
Напряжения кручения в сечении I - I будут определяться по формуле
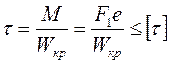. (7.10)
Момент сопротивления сечения I - I вилки лопасти кручению можно определить приравняв это сечение прямоугольнику высотой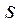 
и шириной 
;
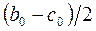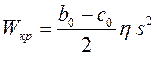(7.11)
где параметры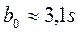 
; а 
.
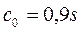Напряжение изгиба в сечении вилки I - I будет равно
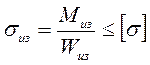(7.12)
Из рис.7.1. видно, что изгибающий момент в сечении I - I равен
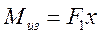; (7.13) где параметр 
.
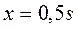Момент сопротивления изгибу прямоугольного сечения вилки лопасти определяют по формуле
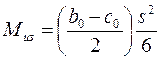. (7.14)
Кроме определения напряжения в сечении I - I, необходимо так же проверить напряжение в сечении II - II.
Это сечение передает полный крутящий момент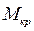 
и в нем возникает только напряжения кручения, которые можно определить по формуле
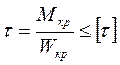; (7.15) где 
.
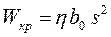Шестеренные и рабочие валки изготавливают как правило как одно целое с лопастями для шарниров шпинделей, поэтому допускаемые напряжения для лопастей надо брать такими же, как и для шеек шестеренных и рабочих валков.
Во многих случаях, особенно когда шейки валков установлены на подшипниках качения лопасти насаживают на концы рабочих или шестеренных валков. В этом случае их изготавливают из такого же материала (сталь 40 или 40Х), как и шпиндели; поэтому допускаемое напряжение для расчета лопастей принимают таким же и при расчете шпинделей.
Отчет о работе должен содержать : тему и цель работы, расчетную часть со всеми пояснениями; в конце работы необходимо сделать вывод, в котором необходимо указать выполнение условий прочности во всех приведенных сечениях. Если условия не выполняются, то необходимо предложить решение возникшей проблемы. Для подготовки к защите ответьте на контрольные вопросы.
Контрольные вопросы :
1) Назовите типы шарниров, применяемых в конструкциях универсальных шпинделей.
2) Объясните принцип действия шарнира Гука.
3) Назовите типы уравновешивающих устройств, применяемых в конструкциях универсальных шпинделей.
Таблица 7.1. Исходные данные для выполнения работы
Вариант
|
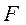
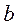
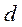
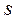
Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|
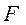
| MH | 5,0 | 5,4 | 4,8 | 5,1 | 5,5 | 5,3 | 4,7 | 5,5 | 5,6 | 6,2 | 4,6 | 5,4 | 5,3 | 5,7 | 5,2 |
|
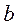
| мм | 460 | 510 | 470 | 480 | 500 | 490 | 450 | 490 | 500 | 550 | 440 | 460 | 500 | 490 | 480 |
|
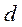
| мм | 300 | 340 | 290 | 300 | 310 | 330 | 260 | 290 | 340 | 340 | 250 | 280 | 320 | 330 | 320 |
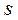
| мм | 180 | 210 | 200 | 205 | 190 | 180 | 150 | 190 | 200 | 210 | 150 | 160 | 170 | 180 | 180 |
При использовании данного метода в курсовом и дипломном проекте геометрические параметры необходимо взять реальные с чертежа шарнира.
Практическая работа № 8
Дата: 2019-03-05, просмотров: 413.
