Пусть в области А микрочастица имеет потенциальную энергию равную нулю, а в области В равную u.
Запишем одномерное амплитудное стационарное уравнение Шредингера:
.
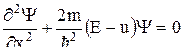Длина волны де Бройля для электрона равна:
.
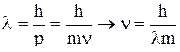Тогда кинетическая энергия:
.
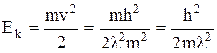Введем волновое число κ=2π/λ
,
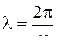откуда
,
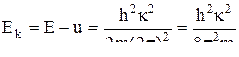где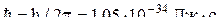 
.
Тогда
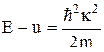. (6)
Выразив из (6) κ получаем:
.
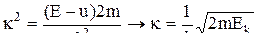Следовательно, уравнение Шредингера можно переписать в виде:
.
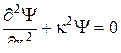В области А Ек=Е, u=0 (Е - полная энергия частицы). Ψ=Ψ1, в области В Ек=Е-u, а Ψ=Ψ2.
Запишем уравнения Шредингера для областей А и В:
А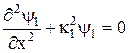 
, (7)
В 
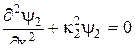, (8)
где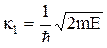 
, 
.
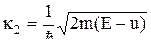Общие решения уравнений (7) и (8) можно записать в виде:
Ψ1=А1exp(ik1x)+B1exp(-ik1x),
Ψ2=А2exp(ik2x)+B2exp(-ik2x),
где А1 – амплитуда падающей волны, В1 – амплитуда отраженной волны в области А; А2 – амплитуда волны, распространяющейся в области В в направлении х; В2 – амплитуда отраженной волны в области В, т.к. область В полубесконечна, то отраженной волны нет и В2=0.
Вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны де Бройля. Тогда
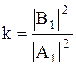
отношение квадрата амплитуды отраженной волны к квадрату амплитуды падающей волны называется коэффициентом отражения микрочастицы от барьера. А отношение квадрата амплитуды прошедшей волны к квадрату амплитуды падающей волны называется коэффициентом прозрачности:
.
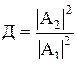Не трудно показать, что
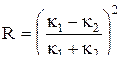, (9)
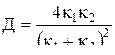. (10)
Если Е > u, то R и Д определяется из (9) и (10) и R+Д=1, т.е. в данном случае в отличие от классической частицы наблюдается отражение. Коэффициент отражения R будет тем больше, чем меньше k2 и следовательно чем меньше разность Е-u.
Если Е=u, то из (8) следует, что k2=0 и тогда R=1, а Д=0, т.е. наблюдается полное отражение волны.
Если Е<u, то k2 (см. (8)) является мнимой величиной.
Обозначим через k вещественную величину
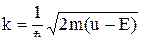
Тогда k2 = i×k
,
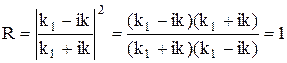(см. определение комплексно-сопряженных чисел).
Д=1-R=0.
Однако в этом случае
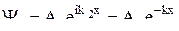
Вероятность обнаружения частицы в области В в зависимости от значения координат будет равна
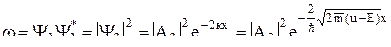. (11)
Произведение комплексно сопряженных чисел есть число действительное и равное квадрату модуля каждого из них.
Комплексно-сопряженными числами называются два числа, действительные части которых равны, а мнимые различаются только знаками.
Выражение (11) показывающее, что вероятность обнаружения частицы в области В отлична от нуля, не противоречит однако Д=1-R, показывающему, что падающая волна полностью отражается от барьера. Дело в том, что некоторая часть частиц из падающего потока проникает в область В, а затем выходит в область А.
Прямоугольный барьер
Пусть в области А и С потенциальная энергия частицы равна нулю, а в области В потенциальная энергия равна u. Ранее было показано, что существует некоторая вероятность нахождения частицы на некотором расстоянии х от прямоугольного барьера при Е<u. Если х>d, то частицы будут из области А переходить в область С.
Такое прохождение частиц через барьер получило название туннельного эффекта. Коэффициент прозрачности барьера в этом случае равен:
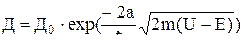
где Д0 – коэффициент пропорциональности, равный ~1.
При туннельном прохождении барьера, энергия микрочастиц не меняется, они покидают барьер с той же энергией, с какой входят в него.
Вероятность прохождения электрона через барьер при Е<U быстро убывает с увеличением толщины барьера.
Глубокая прямоугольная потенциальная яма
В областях А и С потенциальная энергия частицы равна u, а в области В – нулю.
Ширину потенциальной ямы обозначим через а.
Решение уравнения Шредингера показывает, что микрочастица, запертая в потенциальной яме, может иметь только квантованные значения энергии. Каждому значению энергии будет соответствовать собственная волновая функция:
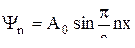
n – квантовое число.
Энергия частицы определяется выражением
.
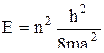Плотность состояний
Как известно, соотношение неопределенностей характеризует область пространственной локализации микрочастицы при заданном интервале проекций импульса.
dx×dpx ≥ h, dy×dpy≥h, dz×dpz ≥ h.
Перемножим левые и правые части неравенств:
dx×dy×dz×dpx×dpy×dpz≥h3.
Обозначим величины неопределенностей, дающих при перемножении точно h3 индексом «0»
dx0×dy0×dz0×dp0x×dp0y×dp0z ≥ h3. (12)
Равенство (12) характеризует минимальную, так называемую фазовую ячейку в шестимерном пространстве координат-импульсов, «разрешенную» частице.
Пусть dz – число минимальных (элементарных) фазовых ячеек в каком-либо объеме dxdydzdpxdpydpz шестимерного пространства координат-импульсов:
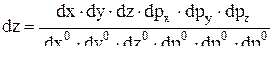
или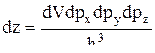 
.
Рассмотрим единичный объем твердого тела dV=1. Тогда число элементарных фазовых ячеек в единичном обычном объеме в некотором объеме трехмерного пространства импульсов равно:
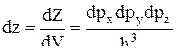
Найдем величину dz в шаровом слое пространства импульсов, ограниченном сферами с радиусами p и p + dp. При этом dpx×dpy×dpz =4πp2dp – объем шарового слоя.
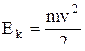, откуда p2=(mv)2=2mEk=2mE. (13)
Ek можно приравнять к Е , т.к. потенциальная энергия свободной частицы равна нулю.
Из (13)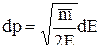 
,
( 
, 
, 
.)
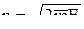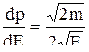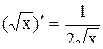Тогда
dpx×dpy×dpz=4πp2dp=4π2mE·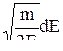 
=2π(2m)3/2·E1/2×dE,
dpx×dpy×dpz =2π(2m)3/2E1/2dE.
Отсюда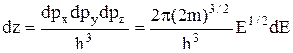 
.
Тогда число элементарных фазовых ячеек, приходящихся на единичный интервал энергии:
.
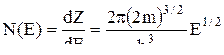N(E) называется плотностью состояний и является полуквадратичной функцией энергии Е. С ростом энергии возрастает и dZ=NdE, т.к. возрастает объем шарового слоя заданной толщины dp с ростом р. Следовательно увеличивается и число элементарных фазовых ячеек.
Функция Ферми
В соответствии с принципом запрета Паули в элементарной фазовой ячейке может находиться не более двух электронов, имеющих антипараллельные спины. Ячейка может быть полностью занята, занята частично, либо полностью свободна.
Из статистической физики известно, что вероятность заполнения электронами фазовой ячейки, имеющей энергию Е, определяется функцией Ферми:
,
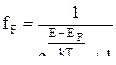где ЕF – энергия Ферми.
При абсолютном нуле функция Ферми fF принимает лишь два значения при Е<ЕF=ЕF0 fF=1,
а при Е>ЕF fF=0. Если Т ≠ 0, то наибольшее изменение fF наблюдается вблизи величины ЕF, а при Е= ЕF fF=1/2.
Интервал изменения fф от 1 до 0 простирается по оси абсцисс в пределах нескольких КТ влево и вправо от ЕF. Грубо можно считать, что при
Е<ЕF-КТ fF=1, а при Е0>ЕF+КТ fF=0.
В условиях термодинамического равновесия уровень Ферми оказывается постоянным в любой системе контактирующих тел. Необходимым условием термодинамического равновесия системы является постоянство уровня Ферми.
Электронный газ, свойства которого описываются функцией Ферми, называют вырожденным или квантованным. При этом число состояний одного порядка оказывается равным с числом частиц. Электронный газ называется невырожденным, если число разрешенных энергетических состояний значительно больше числа электронов, при этом используется классическая статистика Максвелла-Больцмана, поскольку квантомеханические запреты затушевываются.
Электронный газ можно считать невырожденным, если выполняется условие:
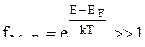
Это условие выполняется при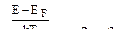 
на хвосте кривой выше ЕF. Этот «хвост» соответствует распределению Максвелла-Больцмана.
Наоборот, при выполнении условия:
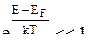
газ является вырожденным.
Концентрация электронного газа
Плотность состояний N определяет число элементарных фазовых ячеек, приходящихся на единичный интервал энергии при расчете на единицу объеме. Вероятность же нахождения электрона в состоянии с энергией Е выражается в виде функции Ферми. Тогда число свободных электронов dn0, энергия которых заключена в интервале от Е до Е + dЕ:
dn0=dz·2fF
т.к.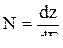 
, то
dn0=N·2fFdE. (14)
Наличия множителя 2 связано с принципом Паули.
Подставим значение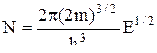 
в (14):
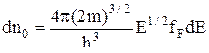, (15)
отсюда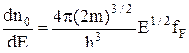 
. (16)
При Т=0 в интервале от 0 до ЕF fF=1. При Т≠0 кривая dn0/dE имеет более сложный вид.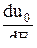 
с ростом Е сначала возрастает в интервале от 0 до Е<ЕF, а затем уменьшается до нуля.
Для определения концентрации свободного вырожденного газа возьмем интеграл по энергии выражения (15) при Т=0
,
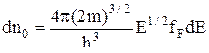откуда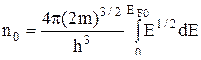 
,
получаем
.
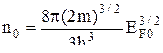Для невырожденного газа можно показать, что
.
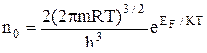Эта формула выражает связь между концентрацией невырожденного газа n0 и уровнем Ферми ЕF.
В металлах находящихся в твердом состоянии электронный газ находится в вырожденном состоянии.
Заметим, что в электропроводности металлов могут принимать участие лишь электроны, располагающиеся вблизи уровня Ферми. Поскольку энергия электрона в электрическом поле увеличивается на величину: ∆Е=еЕl, где е – заряд электрона 1,6·10-19 Кл, Е – напряженность электрического поля, l – длина свободного пробега Е=1В/см l=10-6см, ∆Е=10-6 ЭВ=1,6·10-25 Дж – очень мала.
Поэтому электроны, располагающиеся на уровнях значительно ниже уровня Ферми, не могут участвовать в проводимости, т.к. не могут увеличивать свою энергию на величину энергии дрейфа, поскольку все ближайшие энергетические уровни заняты другими электронами.
Строение атома
Состояния электронов в атомах характеризуются четырьмя квантовыми числами.
1) Главное квантовое число n=1,2,3,4…Оно определяет порядковый номер разрешенной орбиты или энергетического уровня электрона.
2) Орбитальное квантовое число l связано с орбитальным механическим моментом количества движения р электрона …(n-1)l=0,1,2…
Моментом количества движения точки относительно полюса называется вектор, равный векторному произведению радиус-вектора точки, проведенного из полюса, на ее количество движения.
3) Моментное квантовое число m=0, ±1, ±e определяет проекцию момента рi на некоторое направление m принимает лишь целочисленные значения.
4) Спиновое квантовое число S=±½ выражает собственный момент количества движения электрона. Он может быть направлен либо параллельно либо антипараллельно орбитальному моменту количества движения.
Совокупность электронов, обладающих одним и тем же значением главного квантового числа n, образуют слой атома n=1, к – слой, n=2, Н-слой, n=3, μ-слой и т.д.
Внутри слоя электроны с различными орбитальными числами l образуют оболочки S (l=0), p (l=1), d(l=2), f(l=3) и т.д.
Согласно принципу Паули в одном квантовом состоянии, характеризуемом четырьмя квантовыми числами, может находиться не более одного электрона.
При заполнении слоев и оболочек электроны стремятся занять более низкие энергетические уровни.
Приложение 2
Дата: 2019-03-05, просмотров: 187.
