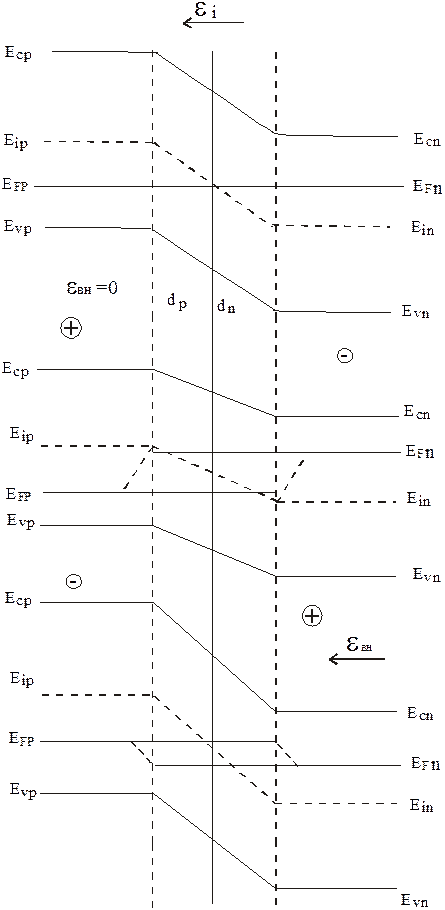
Рассмотрим изменение зонной диаграммы при приложении к р-n-переходу внешнего напряжения. При этом следует иметь в виду, что “плюс” внешнего источника опускает уровни энергии в зонной диаграмме, “минус” - поднимает. При приложении внешнего электрического поля нарушается термодинамическое равновесие и уровни Ферми заменяются на квазиуровни Ферми, т.е. уровни Ферми при определенном поле. Полем в толще полупроводника пренебрегаем, т.е. считаем, что энергетические зоны идут без наклона (горизонтально).
Это означает, что практически все внешнее напряжение падает на переходе, а падение напряжения на электронейтральных частях полупроводника близко к нулю. На рис. 4.8 приведены зонные диаграммы р-n-перехода в равновесном состоянии (а), при прямом (б) и при обратном (в) включении. При наложении внешнего поля в прямом направлении изгиб зон в р-n-переходе уменьшается и становится равен:
| |
| |
|
|
|
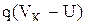, (4.3.1)
где U - внешнее смещение в прямом направлении.
Квазиуровни Ферми для основных носителей заряда в n-области (EFn) и основных носителей в р-области EFp сдвигаются друг относительно друга на qU, т.е.:
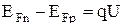. (4.3.2)
Для тонкого р-n-перехода допустимо считать квазиуровень EFn неизменным во всей n-области, а также во всем переходе. Квазиуровень EFp можно считать одинаковым в р-области и во всем р-n-переходе. Пунктиром на рис. 4.8 условно нанесены квазиуровни Ферми для неосновных носителей заряда в каждой из областей. Вдали от р-n-перехода они совпадают с квазиуровнями для основных носителей заряда, т.е. с уровнями Ферми для каждой из областей.
При наложении внешнего поля в обратном направлении (см. рис. 4.8) изгиб зон на р-n-переходе увеличивается и оказывается равным: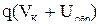 
где Uобр - часть внешнего напряжения подающего на переходе.
ВАХ тонкого р- n -перехода
Тонким р-n переходом называют электронно-дырочный переход, толщина которого столь мала, что можно пренебречь процессами рекомбинации и генерации носителей заряда в области объемного заряда р-n-перехода.
Т.е. если известна плотность потока дырок jp или электронов jn в каком-либо сечении р-n-перехода, то она такова же в любом другом сечении р-n-перехода.
Из формул (4.2.4) и (4.2.5) можно записать концентрацию электронов npгр на границе запирающего слоя в р-области и концентрацию дырок pnгр на границе запирающего слоя в n-области:
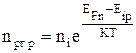, (4.4.1)
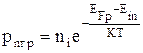. (4.4.2)
При этом Eip и Ein принимают значения соответствующие границам.
Для неосновных носителей заряда вдали от р-n перехода можно записать
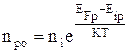, (4.4.3)
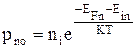. (4.4.4)
В формулах (4.4.3) и (4.4.4) произошла замена квазиуровней по сравнению с формулами (4.4.1), (4.4.2), т.к. в электронейтральной части полупроводника вдали от р-n-перехода в р-области EFp=EFn, а в n-области EFn=EFp.
Разделим левые и правые части выражений (4.4.1) и (4.4.2) друг на друга:
,
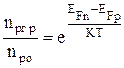откуда
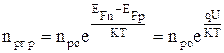. (4.4.5)
Разделим левые и правые части выражений (4.4.3) и (4.2.4) друг на друга:
,
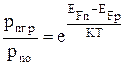откуда
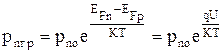. (4.4.6)
При EФn-EФp>0, т.е. при прямом включении р-n-перехода: npгр>npo pnгр>pno.
Избыточная концентрация неосновных носителей заряда на границах в этом случае равна:
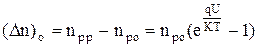, (4.4.7)
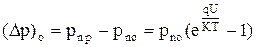. (4.4.8)
Эта избыточная концентрация появляется вследствие инжекции носителей заряда через р-n-переход. Dn и Dp являются функциями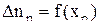 
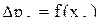. На рис. 4.9. показано изменение избыточной концентрации неосновных носителей от расстояния от области р-n-перехода.
Электроны, инжектированные в р-область, притягивают к себе дырки из объема этой области, так что вне р-n-перехода сохраняется электронейтральность. Недостаток носителей заряда в объеме пополняется через контакт. Аналогично дырки, инжектированные в n-область, притягивают к себе электроны из объема этой области, где также сохраняется электронейтральность. Глубина проникновения инжектированных носителей определяется их рекомбинацией. Неосновные носители рекомбинируют с основными, поэтому концентрация неосновных носителей падает с расстоянием и равна:
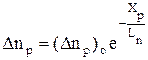, (4.4.9)
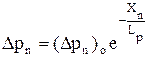. (4.4.10)
где Ln,Lp- расстояние от границы р-n-перехода, на котором концентрации неосновных носителей уменьшаются в е раз, которое называется диффузионной длиной. Заметим, что при приложении прямого смещения запирающий слой сужается. При обратном смещении р-n-перехода он расширяется и: EFn-EFp=qU<0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
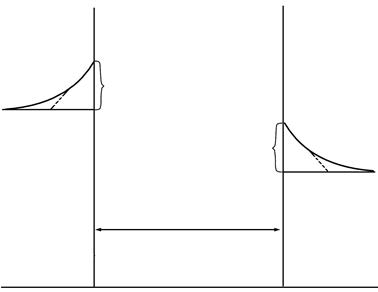
Рис. 4.9
|
|
|
|
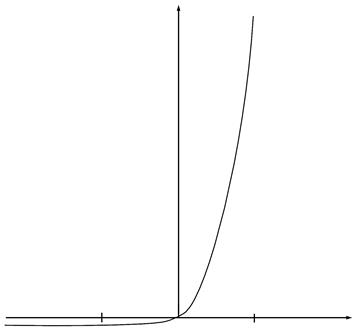
Рис. 4.10
Тогда для обратного включения npгр<npo. В этом случае наблюдается проникновение неосновных носителей заряда через р-n-переход из областей прилегания к р-n переходу. Выражения (4.4.7-4.4.10) сохраняются и в этом случае. Однако, избыточная концентрация здесь имеет отрицательный знак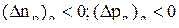 
, т.е. в этом случае мы имеем дело не с избыточной, а с недостаточной концентрацией неосновных носителей.
p-n переход можно считать тонким, если d<Ln и d<Lp, т.е. если толщина перехода меньше диффузионных длин носителей заряда.
Плотность диффузионного тока через границы при любой полярности внешнего напряжения равна:
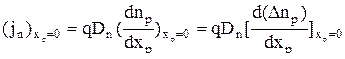, (4.4.11)
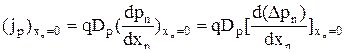. (4.4.12)
Подставим в (4.4.11) и (4.4.12) выражения (4.4.9) и (4.4.10) и получим с учетом (4.4.7) и (4.4.8)
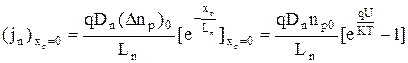, (4.4.13)
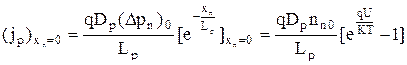. (4.4.14)
Поскольку мы предположили, что плотности электронов и дырок одинаковы в любом сечении р-n-перехода и на его границах, а так же поскольку движение электронов и дырок противоположно друг другу, ВАХ р-n-перехода можно представить в виде:
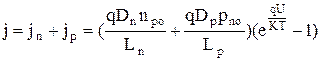, (4.4.15)
С учетом того, что:
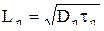, (4.4.16)
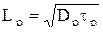, (4.4.17)
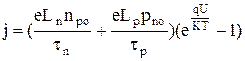. (4.4.18)
Проанализируем (4.4.15).
При обратном смещении на р-n-переходе (U<0)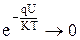 
, а скобка 
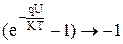, следовательно, обратный ток р-n-перехода стремится к
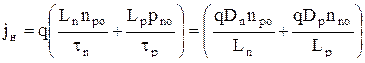. (4.4.19)
Эту плотность тока называют плотностью тока насыщения. Она достигается уже при U»-0,1В. jн определяется концентрацией неосновных носителей и у германиевых р-n-переходов больше, чем у кремниевых.
При прямых смещениях плотность тока через р-n-переход растет по экспоненте и уже при небольших напряжениях достигает большого значения.
Подставляя в (4.4.19), (4.4.18) получим
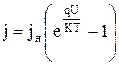. (4.4.18)
На рис. 4.10 показана ВАХ р-n-перехода. Как видно из рисунка р-n-переход обладает ярко выраженной односторонней (униполярной) проводимостью, т.е. проявляет высокие выпрямляющие свойства.
Подчеркнем, что перенос заряда через р-n-переход осуществляется с помощью неосновных носителей, т.к. область р-n-перехода обеднена основными носителями.
Поверхностные явлении
Поверхностные состояния
Рассмотрим процессы на поверхности полупроводника. В 1932 г. советским ученым Таммом было показано, что обрыв решетки приводит к возникновению разрешенных уровней в запрещенной зоне. Уровни Тамма возможны для идеальной поверхности полупроводника. Реальные поверхности покрыты слоем адсорбированных атомов и молекул. Эти примеси также создают поверхностные уровни, которые могут быть как донорными, так и акцепторными. Роль примесей могут играть и различные дефекты решетки. Разрешенные уровни в запрещенной зоне полупроводника на его поверхности называются поверхностными уровнями или поверхностными состояниями.
При высокой плотности поверхностных состояний они, взаимодействуя друг с другом, могут размыться в поверхностную зону. Электроны в этой зоне могут двигаться только вдоль поверхности.
Поверхностные состояния могут захватывать электроны или наоборот отдавать их, заряжаясь положительно или отрицательно. Заряжение поверхности полупроводника при заполнении поверхностных состояний сопровождается возникновением у поверхности слоя объемного заряда, нейтрализующего поверхностный заряд. Нейтрализация происходит путем притяжения к поверхности носителей со знаком заряда противоположным знаку заряда поверхности и отталкивания носителей одного знака. Вследствие этого поверхностный слой обедняется носителями того знака, которым заряжена поверхность и обогащается носителями противоположного знака. При этом наблюдается изгиб зон и возникает поверхностный объемный заряд. Если поверхность полупроводника заряжена отрицательно, то в приповерхностном слое зоны изгибаются вверх, а если положительно то низ.
Эффект поля. МДП-структуры
Измерять объемный поверхностный заряд полупроводника можно с помощью поля, перпендикулярного поверхности. Для создания такого поля в полупроводнике, как правило, используют МДП-структуры (рис. 5.1).
Если к идеальной МДП-структуре прикладывается положительное или отрицательное напряжение, то в приповерхностной области полупроводника могут возникнуть три состояния: обеднение, инверсия и обогащение этой области носителями заряда.
Обедненная основными носителями область появляется в случае, когда на металлический электрод подается потенциал, по знаку совпадающий с основными носителями заряда (рис. 5.1, а и б). Вызванный таким потенциалом изгиб зон приводит к увеличению расстояния от уровня Ферми до дна зоны проводимости в полупроводнике n-типа и до потолка валентной зоны в полупроводнике p-типа. Увеличения этого расстояния сопровождается обеднением приповерхностной области основными носителями.
Когда на металлический электрод подается достаточно большой потенциал по знаку совпадающий с основными носителями (рис. 5.2, в и г), то расстояние от уровня Ферми до потолка валентной зоны в полупроводнике n-типа оказывается меньше расстояния до дна зоны проводимости (рис. 5.2, г), вследствие чего концентрация не основных носителей заряда (дырок) у поверхности полупроводника становится выше концентрации основных носителей и тип проводимости этой области меняется. Изменение типа проводимости полупроводника называется инверсией, а слои, в которых оно наблюдается, называются инверсионными слоями.
Если знак потенциала металлического электрода противоположен знаку заряда основных носителей тока в полупроводнике, то происходит притяжение основных носителей к поверхности и обогащение ими приповерхностного слоя (рис. 5.2, д и е).
С изменением концентрации основных носителей под действием внешнего поля в приповерхностном слое меняется и проводимость. Явление изменения поверхностной проводимости под действием поперечного поля называется эффектом поля.
Дата: 2019-03-05, просмотров: 228.
