Различными видами финансовых контрактов могут предусматриваться различные схемы начисления процентов. Как правило, в этих контрактах оговаривается номинальная процентная ставка, обычно годовая. Эта ставка, во-первых, не отражает реальной эффективности сделки и, во-вторых, не может быть использована для сопоставлений. Для того чтобы обеспечить сравнительный анализ эффективности таких контрактов, необходимо выбрать некий показатель, который был бы универсальным для любой схемы начисления. Таким показателем является эффективная годовая процентная ставка r_e, обеспечивающая переход от Р к F_n при заданных значениях этих показателей и однократном начислении процентов.

Общая постановка задачи может быть сформулирована следующим образом. Заданы исходная сумма Р, годовая процентная ставка (номинальная) r, число начислений сложных процентов т. Этому набору исходных величин в рамках одного года соответствует вполне определенное значение наращенной величины F₁. Требуется найти такую годовую ставку r_е, которая обеспечила бы точно такое же наращение, как и исходная схема, но при однократном начислении процентов, т.е. т = 1. Иными словами, схемы {Р, F₁, r, т > 1} и {Р, F₁, r_e, m = 1} должны быть равносильными.

Из формулы (2.10.6) следует, что в рамках одного года:

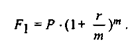
Из определения эффективной годовой процентной ставки следует, что:

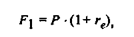
отсюда:

Из формулы (2.10.12) следует, что эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. Кроме того, для каждой номинальной ставки можно найти соответствующую ей эффективную ставку; две эти ставки совпадают лишь при m = 1. Именно ставка r_е является критерием эффективности финансовой сделки и может быть использована для пространственно-временных сопоставлений.

Пример 2.25. Предприниматель может получить ссуду: а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант более предпочтителен?

Относительные расходы предпринимателя по обслуживанию ссуды могут быть определены с помощью расчета эффективной годовой процентной ставки - чем она выше, тем больше уровень расходов. По формуле (2.10.12):

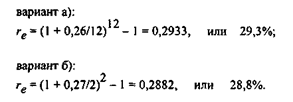
Таким образом, вариант б) является более предпочтительным для предпринимателя. Необходимо отметить, что принятие решения не зависит от величины кредита, поскольку критерием является относительный показатель - эффективная ставка, а она, как следует из формулы (2.10.12), зависит лишь от номинальной ставки и количества начислений.

Понимание роли эффективной процентной ставки чрезвычайно важно для аналитика финансовой службы предприятия. Дело в том, что принятие решения о привлечении средств, например, банковской ссуды на тех или иных условиях, делается чаще всего исходя из приемлемости предлагаемой процентной ставки, которая в этом случае характеризует относительные расходы заемщика. В рекламных проспектах непроизвольно или умышленно внимание на природе ставки обычно не акцентируется, хотя в подавляющем числе случаев речь идет о номинальной ставке, которая может весьма существенно отличаться от эффективной ставки. Рассмотрим простейший пример.

Пример 2.26. Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка равна 10%. По формуле (2.10.12):

Различие между двумя ставками может быть гораздо более разительным при заключении некоторых специальных кредитных договоров, например, при оформлении кредита на условиях добавленного процента.

Сущность этого и подобных договоров подробно рассмотрена в [Ковалев, 1999, с. 652-654].

Математически можно показать, что при m > 1 справедливо неравенство r_е > r, которое, очевидно, следует и из финансовых соображений.

В финансовых соглашениях не имеет значения, какую из ставок указывать — эффективную или номинальную, поскольку использование как одной, так и другой дает одну и ту же (с любой точностью приближения) наращенную сумму. В США в практических расчетах применяют номинальную ставку и, следовательно, формулу (2.10.6). В европейских странах, как правило, вначале определяют эффективную ставку r_е и затем пользуются формулой F_n = Р ∙ (1 + r_е )ⁿ.

Из формулы (2.10.12) следует, в частности, соотношение для определения номинальной ставки, если в контракте указаны эффективная годовая процентная ставка r_е и число начислений сложных процентов m:

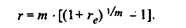
Пример 2.27. Определить номинальную ставку, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно. Поскольку r_e = 0,18 и m = 12, то:

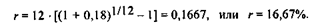
Таким образом, ежегодное начисление сложных процентов по ставке 18% годовых дает тот же результат, что и ежемесячное начисление сложных процентов по ставке 16,67%.