Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является 1 год, наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Известны две основные схемы дискретного начисления:

• схема простых процентов;
• схема сложных процентов.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р, требуемая доходность - r (в долях единицы). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Р ∙ r. Таким образом, размер инвестированного капитала (R_n) через n лет будет равен:

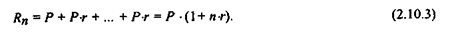
Считается, что инвестиция сделана на условиях сложного процента, если очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором проценты. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:

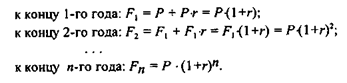
Как же соотносятся величины R_n и F_n? Это чрезвычайно важно знать при проведении финансовых операций. Все зависит от величины п. Сравним множители наращения по простым и сложным процентам, т.е. сравним (1 + п ∙ r) и (1 + r)^п. Очевидно, что при п = 1 эти множители совпадают и равны (1 + r). Можно показать, что при любом r справедливы неравенства (1 + n ∙ r) > (1 + r)ⁿ, если 0 < n < 1 и (1 + п ∙ r) < (1 + r)ⁿ , если n > 1. Итак:

• R_n > F_n при 0 < n < 1;
• R_n < F_n при n >1.

Графически взаимосвязь F_n и R_n можно представить следующим образом (рис. 2.5):

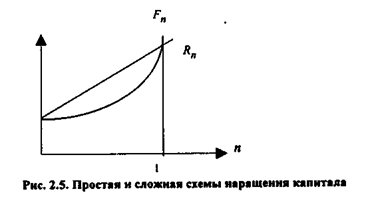
Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

• более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);
• более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);
• обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

В случае краткосрочных ссуд со сроком погашения до одного года в качестве показателя и берется величина, характеризующая удельный вес длины подпериода (дни, месяц, квартал, полугодие) в общем периоде (год). Длина различных временных интервалов в расчетах может округляться: месяц - 30 дней; квартал - 90 дней; полугодие - 180 дней; год - 360 (или 365, 366) дней.

Пример 2.15. Рассчитать наращенную сумму с исходной суммы в 1 тыс. руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20%; б) периоды наращения: 90 дней, 180 дней, 1 год, 5 лет, 10 лет. Полагать, что в году 360 дней.

Результаты расчетов имеют следующий вид:

(тыс. руб.)

Таким образом, если денежные средства размещены в банке на срок в 90 дней (менее одного года), то наращенная сумма составит: при использовании схемы простых процентов - 1,05 тыс. руб.; при использовании схемы сложных процентов - 1,0466 тыс. руб. Следовательно, более выгодна первая схема (разница - 3,4 руб.). Если срок размещения денежных средств превышает один год, ситуация меняется диаметрально: более выгодна становится схема сложных процентов, причем наращение в этом случае идет очень быстрыми темпами. Так, при ставке в 20% годовых удвоение исходной суммы происходит следующим темпом: при использовании схемы простых процентов - за 5 лет, а при использовании схемы сложных процентов - менее чем за четыре года.

Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

В практике деятельности хозяйствующих субъектов часто встречаются финансовые контракты, предусматривающие не единичные выплаты в начале и в конце срока действия контракта, а ряды последовательных выплат. Самым наглядным примером такого денежного потока является кредит, получаемый одномоментно или поэтапно с обязательством погашать его в течение нескольких последовательных периодов заранее оговоренными частями, равными или неравными. Расчеты финансовых характеристик таких денежных потоков аналогичны рассмотренным, с той лишь разницей, что каждая из выплат рассматривается как отдельная и независимая от других. Наращенная или дисконтированная стоимость каждой выплаты определяется по указанным выше формулам, а их приведенные к одному моменту стоимости суммируются.

Формула сложных процентов является одной из базовых формул в финансовых вычислениях, поэтому для удобства расчетов часто пользуются специальными финансовыми таблицами, в которых табулированы значения мультиплицирующих множителей вида (1 + r)ⁿ, и некоторых других.