ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Часть 1
КОНСПЕКТ ЛЕКЦИЙ
Утверждено советом университета
В качестве учебного пособия
Санкт-Петербург
2013
ОГЛАВЛЕНИЕ
Лекция 1. Введение. Аксиомы статики. Приведение систем сил к простейшему виду. Условия равновесия
Лекция 2. Принцип освобождения от связей. Типы связей и их реакции. Схема решения задач статики
Лекция 3. Приведение системы параллельных сил к простейшему виду. Центр тяжести твердого тела и способы определения его положения
Лекция 4. Учет трения в задачах статики
Лекция 5. Кинематика т очки
Лекция 6. Простейшие движения твердого тела
Лекция 7. Плоско - параллельное движение твердого тела
Лекция 8. Общий случай движения твердого тела. Сложное движение точки. Сложение скоростей и ускорений
Лекция 9. Кинематика плоских механизмов. Графоаналитический способ. Математическое моделирование процесса движения
10. Список литературы
Лекция 1.
Введение. Аксиомы статики. Приведение систем сил к простейшему виду. Условия равновесия.
Вопросы и задачи для самоконтроля
1. Какое количество независимых уравнений равновесия (в аналитическом виде) можно записать для системы сходящихся сил, действующих на твердое тело, если все они расположены в одной плоскости?
2. Сформулируйте теорему о трех силах, действующих на твердое тело при его равновесии.
3. Какие аксиомы статики были использованы при нахождении равнодействующей системы сходящихся сил?
4. Как должны были бы располагаться лебедь, рак и щука в басне А.Н.Крылова, при условии, что воз оказался в покое на гладкой горизонтальной поверхности?
5. В каком случае сила не создает момент относительно точки?
6. В каких случаях сила не создает момент относительно оси?
7. Найдите величину момента силы относительно начала координат, если координаты точки и проекции силы известны.
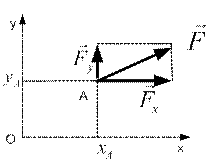
8. Найдите величину момента силы относительно точки О, если величина силы и расстояние ОА, а так же углы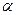 
и 
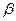с горизонтом известны.
9. Сформулируйте теорему Вариньона.
10. Как вычислить величину момента пары сил, если проекции сил, ее образующих, и координаты точек их приложения известны?
11. Какие из шести проекций необходимы для вычисления момента относительно начала координат силы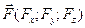 
, приложенной в точке 
?
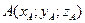12. Сформулируйте лемму о параллельном переносе силы, приложенной к твердому телу.
13. Запишите формулу для вычисления главного вектора системы сил, приложенных к твердому телу, если проекции сил на выбранные координатные оси известны?
14. Запишите формулу для вычисления главного момента системы сил, приложенных к твердому телу, если проекции сил на выбранные координатные оси и координаты точек их приложения сил известны?
15. Для системы из двух сил, изображенной ниже, записать выражения для проекций на ось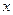 
главного вектора и главного момента.
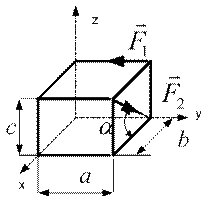
16. Сформулируйте первый инвариант статики.
Лекция 2.
Схема решения задач статики
- выделяем объект, равновесие которого будет рассмотрено (точка, тело или механическая система);
- прикладываем к объекту активные (задаваемые) силы;
- освобождаем объект от связей, заменяя их соответствующими реакциями;
- составляем уравнения равновесия системы сил, приложенных к объекту (в векторном или аналитическом виде);
- решаем уравнения, находя неизвестные (параметры равновесного положения и (или) реакции связей).
ПРИМЕР 4 (задача (4.6) из [ 2 ]). Однородная балка АВ веса Р опирается на две гладкие наклонные направляющие СД и ДЕ, находящиеся в вертикальной плоскости; угол наклона первой из них к горизонту равен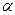 
, второй: 90- 
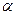. Найти угол 
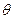наклона балки к горизонту в положении равновесия и давление ее на направляющие.
Реакции в точках касания балки и гладких направляющих направлены по нормали к поверхностям последних; тогда точка пересечения направлений реакций К является вершиной прямоугольника АКВД. В случае равновесия балки по теореме о трех силах вертикальная линия силы веса так же должна проходить через эту точку. Очевидно, что точка О приложения веса однородной балки делит ее пополам, 
т.е. АО=ОВ. В таком случае она является точкой пересечения диагоналей прямоугольника АКВД. Итог рассуждений отображен на рис. 24.
Из рисунка видно, что треугольник АОД равнобедренный. Тогда должны быть равны углы при его основании, т.е. угол ОАД равен углу ОДА. Это равенство позволяет записать уравнение для вычисления угла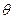 
как
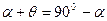; отсюда 
,
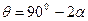Запишем уравнения равновесия для системы сил, действующих на балку АВ:
.
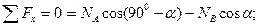
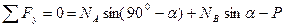Решив систему, получим, что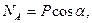 
.
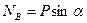ПРИМЕР 5 (задача 4.16 из [ 2 ]). Шлюпка висит на двух шлюпбалках, причем вес ее, равный 9.6 кН, распределяется между ними поровну.
Шлюпбалка АВС нижним полушаровым концом опирается на подпятник А и на высоте 1.8 м над ним свободно проходит через подшипник В; вылет шлюпбалки равен 2.4 м. Пренебрегая весом шлюпбалки, определить силы ее давления на опоры А и В.
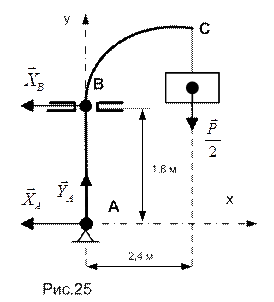
Схематично изобразим шлюпбалку с действующими на нее опорными реакциями (см. рис. 25) и запишем уравнения равновесия полученной плоской системы сил:
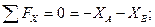
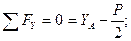
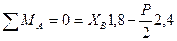
Решив систему относительно неизвестных составляющих опорных реакций, получим:
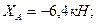
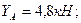
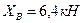
Теперь вычислим силы давления в опорах А и В, как
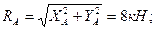
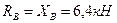
ПРИМЕР 6. Плоская конструкция состоит из трех стержней, соединенных в точке В шарниром. Конец А стержня АВ жестко заделан в вертикальную стену, а концы С и Д стержней ВС и ВД опираются, соответственно, на вертикальную и горизонтальную шарнирно – подвижные опоры. Размеры элементов конструкции и приложенная к ней нагрузка указаны на рис. 26.
Составить систему уравнений для нахождения опорных реакций в точках А, Д и С.
Мысленно освободив конструкцию от опор, заменим их действие пятью неизвестными реакциями (две силы и момент в точке А и по одной силе в точках С и Д). Запись трех уравнений равновесия для плоской системы сил, действующей на конструкцию в целом, не позволяет вычислить искомые неизвестные.
Учтем следующее соображение: если конструкция в целом находится в равновесии, то и каждый из ее элементов должен так же находиться в равновесии (т.е. для системы сил, действующих на каждый элемент, можно записать уравнения равновесия).
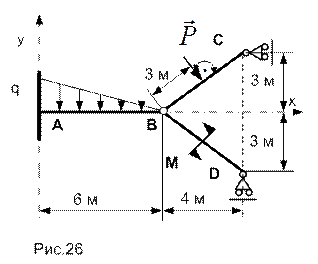
Тогда либо к уравнениям равновесия конструкции в целом добавляют недостающее число уравнений равновесия для ее элементов, либо записывают уравнения равновесия для каждого из элементов, формирующих конструкцию. В рассматриваемом примере выбран второй путь; соответствующие силовые схемы приведены на рис. 27.а,б,в (при этом распределенная по линейному закону нагрузка заменена соответствующей равнодействующей).
Для каждого из элементов и узла сочленения (шарнир В), запишем уравнения равновесия:
Стержень АВ:
.
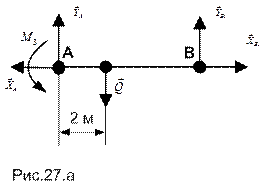
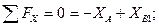
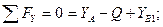
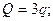
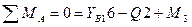Стержень ВС:
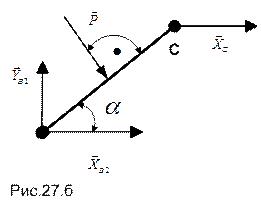
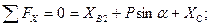
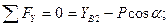
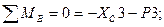
где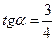 
=0,75
Стержень ВД:
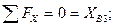
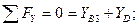
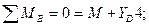
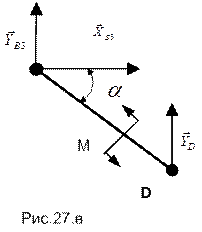
Шарнир В:
.
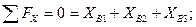
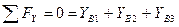Решив систему уравнений, найдем искомые составляющие опорных реакций:
.
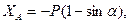
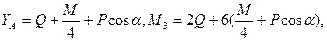
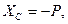
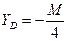Замечание:
- если в узле сочленения соединяются два элемента, то условия равновесия в узле обычно не записываются, а на силовых схемах элементов сразу учитывается 4-я аксиома (третий закон Ньютона) о силах действия и противодействия.
Вопросы и задачи для самоконтроля
1. Какова размерность давления воды на днище судна в системе СИ?
2. Какова размерность жесткости спиральной пружины в системе СИ?
3. В каком случае две силы, приложенные к абсолютно твердому телу, называют уравновешенными?
4. В каком случае две системы сил, приложенных к абсолютно твердому телу, называют эквивалентными?
5. Какие аксиомы статики позволяют моделировать силу скользящим вектором при анализе условий равновесия твердого тела?
6. Какая аксиома статики позволяет находить равнодействующую двух сил, приложенных в одной точке?
7. Какая аксиома статики позволяет рассматривать равновесие системы из твердых тел?
8. Сформулируйте принцип освобождения от связей.
9. Для тяжелого стержня ОВ укажите опорные реакции (или их составляющие), при условии гладкости опорной поверхности.
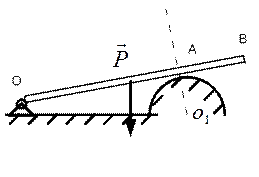
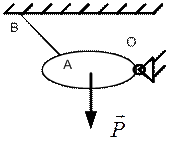
10. Для тяжелого тела, прикрепленного шарниром в точке О к стене и нитью АВ к потолку, укажите опорные реакции (или их составляющие).
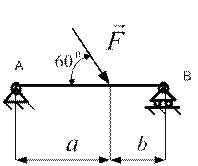
11. На стержень АВ, жестко заделанный в вертикальную стену, действует равномерно распределенная нагрузка интенсивностью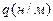 
. Какие усилия следует приложить в точке А, если полагать стержень свободным?
12. Какие модели элементов конструкции обычно рассматриваются в качестве объектов равновесия?
13. Что следует сделать с распределенной нагрузкой при получении системы сил, приложенных к объекту равновесия?
14. Как следует направлять оси координатной системы, что бы уравнения равновесия содержали меньшее число неизвестных?
15. Следует ли записывать все независимые уравнения равновесия, если требуется нахождение только одной опорной реакции?
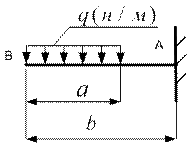
16. Определите опорную реакцию в шарнирно-подвижной опоре В.
Лекция 3.
Приведение системы параллельных сил к простейшему виду. Центр тяжести твердого тела и способы определения его положения
Вопросы и задачи для самоконтроля
1. Верна ли приведенная ниже формула для нахождения абсциссы центра параллельных сил?
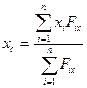
2. Получите самостоятельно формулы для равнодействующей и абсциссы центра приложения нагрузки, равномерно распределенной вдоль оси абсцисс.
3. Прямоугольный понтон имеет длину L , ширину B и осадку T. Определите величины равнодействующих сил давления воды на борта и днище понтона, а так же координаты точек приложения этих сил.
4. Как изменились бы формулы, полученные при решении примера 8, если бы тонкая пластина состояла из элементов с разными удельными весами (например, удельный вес прямоугольника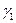 
, а треугольника - 
)?
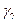5. Определите координаты центра тяжести тонкой однородной пластины прямоугольной (треугольной) формы.
6. Определите аппликату центра тяжести однородного прямоугольного параллелепипеда (пирамиды, кругового конуса).
Лекция 4
Трение скольжения
Обсуждение закономерностей, называемых законами трения скольжения, было начато еще в школьном курсе физики. Коротко напомним их.
1. При стремлении сдвинуть одно тело по поверхности другого возникает реакция, которую принято раскладывать на силу нормального давления к опорной поверхности и силу трения скольжения; при этом последняя направлена в сторону, противоположную тому направлению, в котором действующие на тело задаваемые силы стремятся его сдвинуть. Величина силы трения может принимать значения от нуля до предельной силы трения.
2. Предельное значение силы трения численно равно произведению статического коэффициента трения на силу нормального давления:
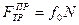(19)
Статический коэффициент трения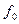 
- величина безразмерная; он определяется опытным путем и зависит от материалов соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность и т.п.).
Так, для пары дерево по дереву, значение коэффициента 0.4-0.7, для металла по металлу 0.15-0.25, для стали по льду 0.027.
3. При сохранении величины силы нормального давления значение предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся поверхностей.
Из первых двух законов следует, что при равновесии
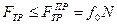
Если найденная в результате расчета величина силы трения не превышает значения предельной силы трения, то имеет место равновесие системы сил, приложенных к телу. Если найденное значение превышает предельную силу трения, то тело начинает движение; при этом величину силы трения следует принять равной произведению динамического коэффициента трения на силу нормального давления. Динамический коэффициент трения так же является величиной безразмерной и определяется опытным путем. Его значение зависит от материала и состояния поверхностей; в большинстве случаев при сухом трении с ростом скорости движения тела значение коэффициента сначала несколько убывает, а затем сохраняет почти постоянное значение, мало отличающееся от статического коэффициента трения .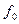
ПРИМЕР 9 (задача 5.41 из [ 2 ]). При взаимодействии с ледовым покровом ледокол рассматривается в равновесии под действием веса судна G, силы поддержания R, упора винтов T, а так же сил, действующих со стороны льда в точке К форштевня: силы нормального давления N и максимальной силы трения F. Угол наклона форштевня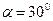 
, коэффициент трения 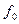= 0.2. Известны значения G= 6000 кН, T = 200 кН, a = 20м, b = 2м, c = 1м. Пренебрегая дифферентом судна, определить вертикальное давление судна на ледяной покров Р, силу поддержания R и расстояние ее от центра тяжести судна d.
На рисунке 35 изображен ледокол и силы, на него действующие.
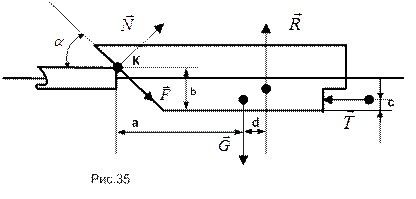
Для плоской системы сил запишем три уравнения равновесия:
.
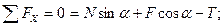
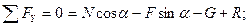
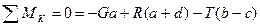Дополним систему условием для предельной силы трения:
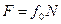
Решим полученную систему уравнений относительно неизвестных:
N = 386.6 кН; F = 7.7 кН; R = 5770 кН; d= 0.83 м.
 |
Теперь можно вычислить вертикальное давление на ледяной покров как
ПРИМЕР 10. На шероховатой поверхности, образующей угол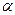 
с горизонтом, находится груз веса Р. Коэффициент трения 
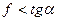. Груз удерживается на наклонной плоскости нитью, перекинутой через блок; к противоположному концу нити подвешен груз веса Q (см. рис.36). Каков должен быть вес подвешенного груза, чтобы груз Р оставался неподвижным?
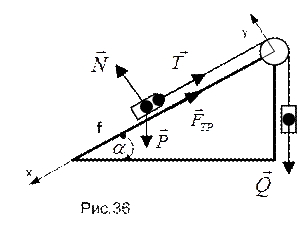
Рассмотрим равновесие груза Р в предположении, что он стремиться сдвинуться вниз по наклонной плоскости. Схема действующих на него сил указана на рисунке. Отметим, что сила натяжения нити численно равна весу груза Q, а условие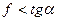 
означает, что предельная сила трения меньше скатывающей силы, т.е. 
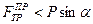(в противном случае груз покоился бы даже при Q = 0 ) . Запишем уравнения равновесия, дополнив их условием для предельной силы трения:
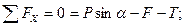
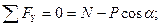
Тогда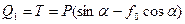 
Теперь рассмотрим равновесие груза Р в предположении, что он стремится сдвинуться вверх по наклонной плоскости.
Схема действующих на него сил будет отличаться от уже рассмотренной изменением направления силы трения на противоположное. Смена знака приведет к иному значению величины подвешенного груза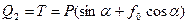 
.
Таким образом, любое значение веса подвешенного груза, находящееся в диапазоне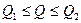 
, сохраняет равновесие груза на плоскости ( при условии ).
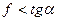Трение качения
Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.
Рассмотрим круглый цилиндр радиуса R и веса P, лежащий на горизонтальной и шероховатой поверхности. Приложим к оси цилиндра горизонтальную силу T, не достаточную для начала скольжения цилиндра по поверхности (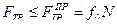 
). Реакция от взаимодействия цилиндра с поверхностью должна быть приложена в точке их соприкосновения А; ее составляющие - сила нормального давления и сила трения (см. рис. 38).
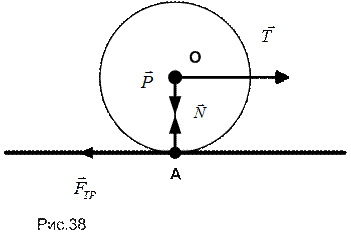
При такой силовой схеме цилиндр должен катится при любой, сколь угодно малой, силе Т, что противоречит нашему опыту. Отмеченное противоречие возникло вследствие использования моделей в виде абсолютно твердых тел, соприкасающихся между собой в одной точке. Фактически из-за деформации соприкосновение происходит вдоль некоторой площадки, смещенной в сторону качения.
Учтем это обстоятельство, перенеся в ту же сторону на некоторое расстояние k точку приложения реакции поверхности (точка В на рис. 39.а).
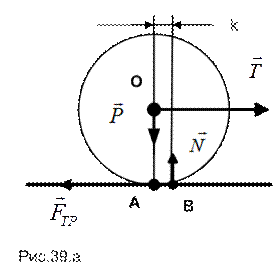
Проведенные эксперименты показывают, что с ростом величины силы Т величина k возрастает до некоторого предельного значения, называемого коэффициентом трения качения, после чего качение начинается. Ниже приведены значения этого коэффициента (в сантиметрах) для некоторых материалов:
Дерево по дереву 0,05 – 0,08
Сталь мягкая по стали
(колесо по рельсу) 0,005
Сталь закаленная по стали
(шариковый подшипник) 0,001
Иногда удобно осуществить учет трения качения добавлением момента пары сил, называемого моментом трения качения и равным, соответственно
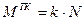(22)
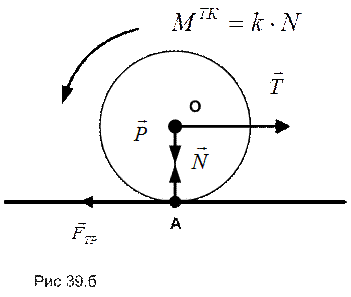
Очевидно, что силовые схемы, изображенные на рисунках 39.а и 39.б эквивалентны.
Сравнение силовых схем рисунков 38 и 39.б показывает, что учет дополнительного фактора (деформация взаимодействующих при качении поверхностей) осуществлен нами добавлением момента трения качения к используемой ранее модели взаимодействия абсолютно твердых тел.
ПРИМЕР 12. На горизонтальной плоскости лежит каток радиуса R=5 cм и веса Р. Коэффициент трения скольжения катка о плоскость 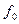= 0.2 , коэффициент трения качения к = 0.005 cм. Определить наименьшую горизонтальную силу Т, перпендикулярную оси катка, при которой каток начинает движение.
На рисунке изображен каток и схема действующих на него сил. Запишем уравнения равновесия:
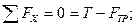
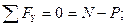
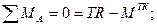
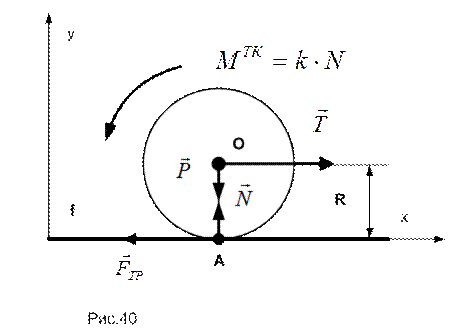
Дополнив систему выражением для предельного момента трения качения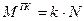 
,
найдем значение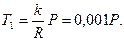 
Дополнив систему выражением для предельной силы трения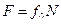 
,
найдем значение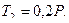 
Вывод: При значениях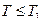 
каток покоится,
При значениях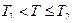 
каток катится без скольжения,
При значениях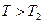 
каток катится со скольжением.
Так как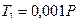 
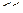
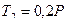, качение начинается при существенно меньшей горизонтальной силе. Именно это обстоятельство обуславливает замену подшипников скольжения на подшипники качения в ситуациях, когда такая замена технически осуществима.
Вопросы и задачи для самоконтроля
1. Какова размерность коэффициента трения скольжения?
2. Какова размерность коэффициента трения качения?
3. Можно ли использовать формулу (19), если сила трения не достигла предельного значения? Как в этом случае определить величину силы трения?
4. Определить минимальную ситу натяжения нити, необходимую для начала движения вверх бруска веса Р по наклонной шероховатой плоскости.
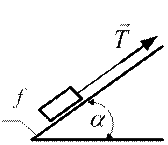
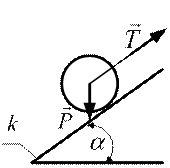
5. Выберете вариант вычисления силы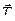 
, необходимой для начала качения колеса без проскальзывания вверх по наклонной плоскости. Вес колеса Р, его радиус 
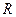, угол наклона 
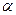и коэффициент трения качения 
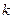известны.
Лекция 5
Кинематика точки
Задание положения точки. Естественный трехгранник кривой и его оси
В технических приложениях выделяется круг задач о движении точки по заранее известной траектории (в общем – криволинейной). В таких случаях для описания движения точки достаточно задаться лишь одной криволинейной координатой – длиной дуги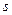 
, измеряемой вдоль траектории от избранного на траектории начала 
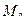(рис.46).
Движение точки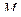 
определится законом изменения дуги как функции времени
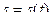. (31)
Дуговая координата 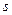точки, в общем случае, отличается от пройденного пути, который является неубывающей функцией времени (они совпадают при условии движения точки по траектории только в одну сторону).
Для определения скорости и ускорения несвободной точки напомним некоторые сведения из дифференциальной геометрии пространственных кривых.
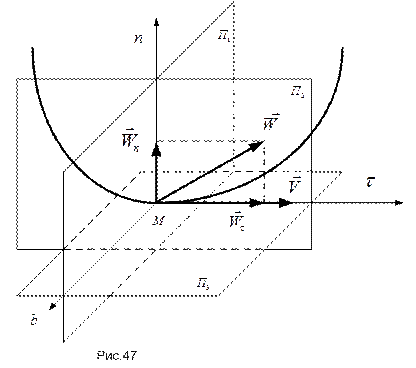
Плоскость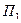 
, перпендикулярная касательной 
к траектории в точке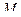 
, называется нормальной плоскостью (рис.47). Любая прямая, лежащая в этой плоскости и проходящая через точку 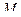, направлена по нормали к кривой.
Касательную к траектории в точке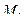 
, близко расположенной к точке 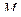, обозначим 
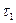, а дугу 
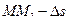(см. рис.46).
Если перенести прямую 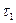параллельно самой себе в точку 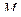, то можно провести плоскость, содержащую прямые и 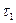; угол 
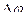между этими прямыми называется углом смежности. С уменьшением 
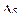до нуля эта плоскость, поворачиваясь вокруг прямой , приближается к некоторому предельному положению – соприкасающейся плоскости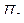 
(см. рис.46). Прямая, по которой пересекаются нормальная и соприкасающаяся плоскости, называется главной нормалью к кривой в точке 
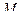. Нормаль, перпендикулярная главной нормали, называется бинормалью кривой. Плоскость 
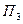, проходящая через касательную и бинормаль в точке М, называется спрямляющей плоскостью.
Нормальная, соприкасающаяся и спрямляющая плоскости образуют естественный трехгранник кривой в точке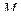 
, а оси 
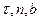являются его осями. Единичные орты этих осей образуют ортонормированный базис локальной естественной координатной системы.
Скорость и ускорение точки
Найдем проекции векторов скорости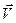 
и ускорения 
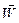точки в естественном базисе.
Радиус-вектор точки 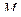представляет собой сложную функцию времени 
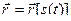, поэтому
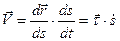. (32)
При выводе формулы учтено, что
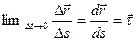- является единичным ортом касательной к траектории движения точки .
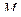По определению ускорения имеем
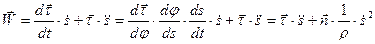. (33)
При выводе формулы учтено, что, во-первых,
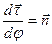- есть орт главной нормали, а, во-вторых, кривизна траектории 
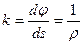, где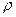 
- радиус кривизны траектории в точке .
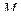Для доказательства первого обстоятельства продифференцируем по углу смежности скалярное произведение
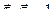. Получим, что 
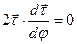, т.е. скалярное произведение двух векторов, расположенных в соприкасающейся плоскости, равно нулю. Это возможно только в случае их ортогональности.
Величина проекции ускорения на касательную
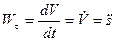называется касательным ускорением, оно характеризует изменение вектора скорости по величине. Величина проекции ускорения на главную нормаль
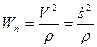называется нормальным ускорением, оно характеризует изменение вектора скорости по направлению. Нормальное ускорение всегда направлено к центру кривизны траектории.
Полное ускорение точки 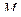равно
.
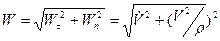Заметим, что в выбранной координатной системе отсутствуют проекции скорости на главную нормаль и бинормаль, а так же проекция на бинормаль ускорения точки.
Рассмотрим несколько частных случаев движения точки.
1.Равномерное движение точки по прямой. Скорость движения не изменяется, поэтому равно нулю касательное ускорение.
Нормальное ускорение так же равно нулю (бесконечно большой радиус кривизны). Тогда
.
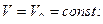
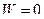2.Равнопеременное движение по прямой (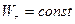 
). Нормальное ускорение равно нулю. Тогда
; 
.
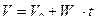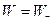3. Равномерное движение по окружности радиуса 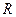. Вектор скорости направлен по касательной к окружности (к радиусу - под прямым углом). Скорость движения не изменяется по величине, поэтому равно нулю касательное ускорение. Полное ускорение равно нормальному, т.е. 
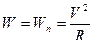. Ускорение направлено к центру окружности.
4. Равнопеременное движение по окружности радиуса 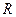. В этом случае скорость изменяется и по величине и по направлению, поэтому
; ; 
; 
.
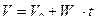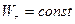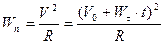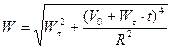ПРИМЕР 15. Центр тяжести катера, разгоняющегося из состояния покоя, описывает дугу окружности радиуса R=75м. Его касательное ускорение изменяется по закону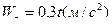 
. Определить скорость и ускорение центра тяжести катера в момент, когда он пройдет путь 50 м.
РЕШЕНИЕ. Интегрируя условие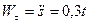 
дважды по времени с учетом нулевых начальных условий, получим:
; 
.
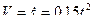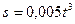Значение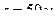 
достигается в момент времени 
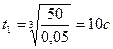. При этом скорость центра тяжести катера будет 
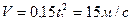, а касательное ускорение - 
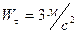. Тогда полное ускорение равно
.
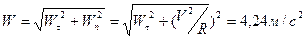5.4. Связь кинематических характеристик при различных способах задания положения точки
В качестве примера разберем переход от задания положения точки в декартовой координатной системе к ее заданию в естественной координатной системе, а так же выведем формулы связи между соответствующими кинематическими характеристиками.
Пусть заданы уравнения движения точки в декартовой координатной системе 
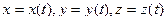. Как уже говорилось выше, будем полагать эти функции дважды дифференцируемыми по времени.
Записанные уравнения могут быть трактованы как уравнения траектории точки в параметрической форме. Если удается исключить из этих уравнений время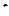 
, то комбинации любых двух полученных соотношений 
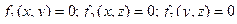задают траекторию движения точки явно как линию пересечения соответствующих поверхностей.
Для траектории движения, расположенной в одной плоскости (ее всегда можно совместить с плоскостью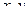 
), достаточно записать первые два уравнения либо получить 
.
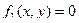Координаты точки начала движения получаются подстановкой начального времени (обычно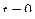 
) в уравнения движения, а анализ изменения координат с ростом параметра 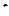определяет положительность или отрицательность направления движения вдоль траектории.
Теперь получим зависимость криволинейной координаты от времени. Для этого воспользуемся формулами для вычисления скорости точки в декартовой и естественной координатных системах:
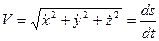(34)
Разделим переменные и возьмем интегралы от правой и левой частей равенства. Получим
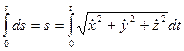(35)
ПРИМЕР 16. По заданным уравнениям движения точки на плоскости
; 
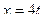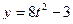
найти ее траекторию, указать начало движения, его положительное направление, а так же получить закон изменения во времени криволинейной координаты точки.
РЕШЕНИЕ. Исключим время из уравнений движения точки, выразив время 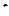из первого уравнения и подставив его во второе уравнение. Получим уравнение параболы 
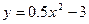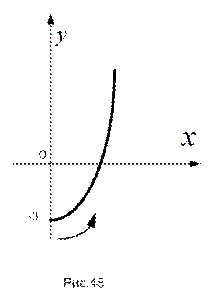
. Так как время не может быть отрицательным (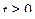 
), траектория точки – правая ветвь параболы (см. рис.48).
Подставив 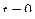в уравнения движения, получим координаты точки начала движения:
; 
.
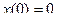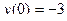Анализ изменения координат при возрастании времени показывает, что и абсцисса и ордината точки возрастают; что соответствует движению точки от начального положения вправо вверх (на рисунке положительное направление движения указано стрелкой).
Для получения закона изменения криволинейной координаты от времени сначала найдем выражения для соответствующих проекций скорости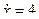 
; 
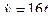, а затем воспользуемся соотношением (2.4). Тогда
.
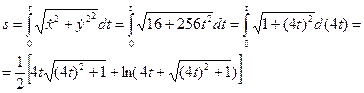ПРИМЕР 17. По заданным уравнениям движения точки на плоскости
; 
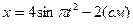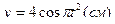
найти ее траекторию, указать начало движения и его положительное направление, а так же записать закон изменения во времени криволинейной координаты точки.
РЕШЕНИЕ. Для исключения времени из уравнений движения воспользуемся известным тригонометрическим соотношением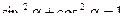 
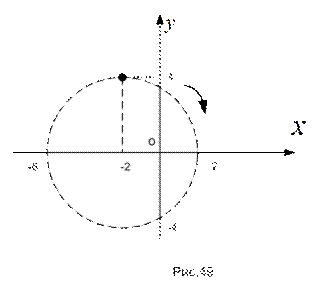
. В этом случае уравнение траектории будет иметь вид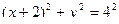 
(окружность радиуса 4 см, сдвинутая на 2 см вдоль оси абсцисс влево, изображена на рис.49).
Подставив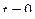 
в уравнения движения, получим координаты точки начала движения:
; 
.
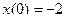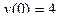Анализ изменения координат при возрастании времени показывает, что абсцисса точки возрастает, а ордината убывает; что соответствует движению точки от начального положения вправо вниз (на рисунке положительное направление движения указано стрелкой).
Для получения закона изменения криволинейной координаты от времени сначала найдем выражения для соответствующих проекций скорости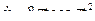 
; 
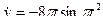, а затем воспользуемся соотношением (6.4). Тогда
.
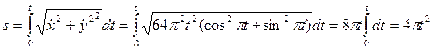Формула (2.4) показывает связь между вычислением скорости точки в декартовой и естественной координатных системах
.
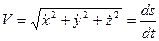Для получения связи между вычислением ускорения точки в указанных координатных системах запишем формулы для его касательной и нормальной составляющих ускорения через проекции скорости и ускорения на оси декартовой координатной системы:
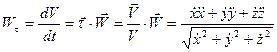(36)
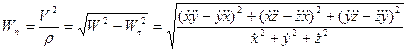
(37)
Радиус кривизны траектории в рассматриваемой точке может быть вычислен как
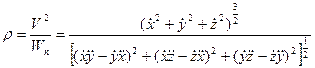(38)
ПРИМЕР 18. Продолжить решение предыдущего примера, определив положение точки М и вычислив в декартовой и естественной координатных системах ее скорость и ускорение в момент времени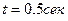 
.
РЕШЕНИЕ. Для определения положения точки М подставим 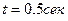в уравнения движения точки:
; 
.
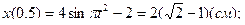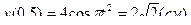Теперь вычислим проекции скорости и ускорения точки М в декартовой координатной системе, взяв соответствующие производные по времени от уравнений движения точки и подставив в них время 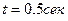. Тогда получим:
.
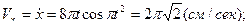
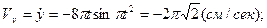
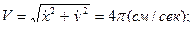
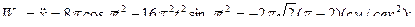
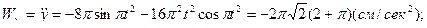
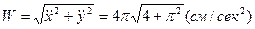Все вычисленные характеристики нанесены на рис.50.
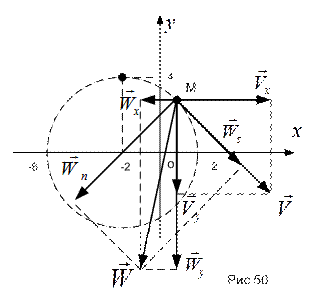
Для определения положения точки М на окружности подставим 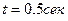в закон изменения криволинейной координаты:
.
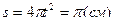Поскольку длина окружности радиуса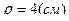 
будет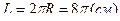 
, то точка М за указанное время прошла в положительном направлении одну восьмую часть окружности.
Теперь вычислим скорость и проекции ускорения точки на оси естественной координатной системы, взяв соответствующие производные от полученного выше закона изменения криволинейной координаты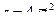 
:
.
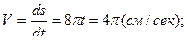
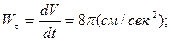
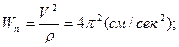
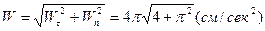При желании можно убедиться, что вычисления по формулам (36, 37 и 38) совпадают с полученными результатами.
Все вычисленные кинематические характеристики так же нанесены на рис.50.
ПРИМЕР 19. Продолжить решение примера 16, определив положение точки М и вычислив в декартовой и естественной координатных системах ее скорость и ускорение в момент времени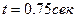 
.
РЕШЕНИЕ. Для определения положения точки М в декартовой координатной системе подставим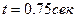 
в уравнения движения точки:
; 
.
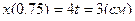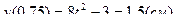Теперь вычислим проекции скорости и ускорения точки М, взяв соответствующие производные по времени от уравнений движения точки и подставив в них время 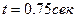. Тогда получим:
.
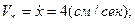
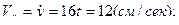
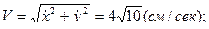
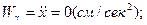
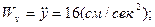
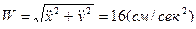Для вычисления касательной и нормальной проекций ускорения и радиуса кривизны траектории в точке М воспользуемся формулами (36, 37 и 38). В случае движения точки по плоскости формулы примут более простой вид:
;
;
.
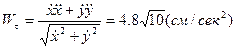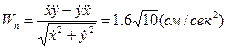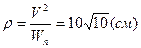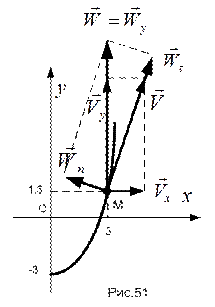
Все вычисленные характеристики нанесены на рис.51.
Вопросы и задачи для самоконтроля
1. Запишите формулы для скорости и ускорения точки при векторном способе задания ее положения. Каковы достоинства и недостатки этого способа?
2. В каком случае величины средней скорости точки и скорости в данный момент времени совпадают?
3. Запишите формулы для проекций скорости и ускорения точки при задании ее положения в декартовой системе координат.
4. Вычислите величину скорости точки через 1 секунду после начала движения, если ее положение на плоскости 
задано радиусом – вектором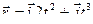 
, где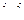 
- орты координатных осей. Размерность проекций радиуса – вектора - метр, времени – секунда.
5. Что должно быть известно при естественном способе задания положения точки?
6. Что характеризует нормальная составляющая ускорения? Запишите формулу для ее вычисления. Как направлена эта составляющая по отношению к траектории?
7. Что характеризует касательная составляющая ускорения? Запишите формулу для ее вычисления.
8. Как движется точка по траектории, если скорость и касательная составляющая ускорения сонаправлены? Если они направлены в разные стороны?
9. Чему равна проекция ускорения точки на бинормаль?
10. По какой траектории движется точка, если векторы ее скорости и ускорения сонаправлены?
Лекция 6:
Вопросы и задачи для самоконтроля
1. Дайте определение поступательного движения тела. Что можно сказать о траекториях, скоростях и ускорениях точек при таком движении тела?
2. Может ли быть окружность траекторией движения точек тела при поступательном движении? Каким будет движение подвесной кабины колеса обозрения?
3. Что можно сказать о глобальных и локальных кинематических характеристиках при поступательном движении тела?
4. Дайте определение вращательного движения тела. Сколько степеней свободы имеет тело в этом случае? Каковы его глобальные характеристики? Может ли ось вращения быть вне границ тела?
5. Как связаны величины локальных и глобальных кинематических характеристик при вращательном движении? Запишите формулы для величин скорости, осестремительной и вращательной составляющих ускорения точки, полного ускорения точки.
6. Как связаны векторы локальных и глобальных кинематических характеристик? Запишите формулы для векторов скорости, осестремительной и вращательной составляющих ускорения точки.
7. Что можно сказать о скоростях в точках контакта элементов, образующих простейшие механические передачи?
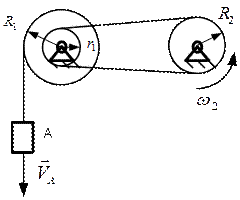
8. Найти угловую скорость 
колеса 2, если известна скорость груза А и радиусы колес (нити полагать нерастяжимыми, проскальзывание – отсутствующим)?
Лекция 7
Вопросы и задачи для самоконтроля
1. Дайте определение плоско – параллельного движения тела. Сколько степеней свободы, в общем случае, имеет при этом тело?
2. В чем суть метода полюса? Какие кинематические характеристики при таком движении являются глобальными? Что происходит с ними при смене полюса?
3. Запишите формулы для вычисления локальных кинематических характеристик по методу полюса.
4. Что такое «мгновенный центр скоростей» тела и как найти точку его расположения? Вычисление скоростей точек плоской фигуры при использовании этого понятия.
5. Теорема о проекциях скоростей точек плоской фигуры на линию, их соединяющую.
6. Найти скорость ползуна В плоского механизма в указанном положении, если скорость 
ползуна А известна?
При решении сначала использовать методом полюса, потом найти мгновенный центр скоростей и воспользоваться им, затем использовать теорему о проекциях скоростей плоской фигуры. Сравнить трудоемкость получения результата различными приемами.
Лекция 8
Вопросы и задачи для самоконтроля
1. Дайте определения абсолютного, относительного и переносного движений точки.
2. Что происходит с параметрами переносного движения при рассмотрении картины относительного движения (и наоборот)?
3. В каком случае производные, вычисленные в неподвижной и подвижной координатных системах, оказываются равными?
4. Запишите формулы, связывающие скорости и ускорения в подвижной и неподвижной системах отсчета.
5. Запишите формулу для вычисления ускорения Кориолиса. В каких случаях оно обращается в нуль?
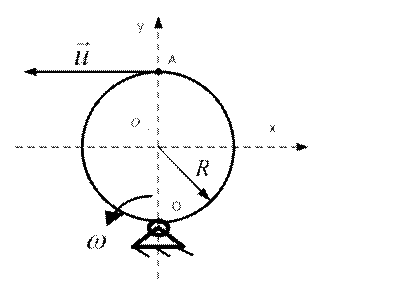
6. Диск равномерно вращается вокруг оси, перпендикулярной его плоскости и проходящей через точку О обода. По ободу с постоянной по величине скоростью 
движется точка А. Найти ускорение точки А в указанном положении.
Лекция 9
Постановка задачи
Кинематический анализ систем со связями является одной из наиболее распространенных в технике задач. Типичными примерами несвободных систем являются плоские механизмы.
Плоским механизмом называется система сопрягающихся абсолютно твердых тел, совершающих плоское поступательное, вращательное и плоскопараллельное движения. Эти тела обычно называют звеньями механизма. Наиболее простыми примерами плоских механизмов являются колесо, катящееся без скольжения и кривошипно-шатунный механизм (рис.75.а, 76.а). Сложные механизмы обычно представляют собой механическое соединение более простых.
Выполнение кинематического расчета подразумевает получение кинематических характеристик звеньев механизма и некоторых точек, им принадлежащих.
Если требуется выполнить кинематический расчет для заданного момента времени (либо определенного положения плоского механизма), обычно используют графоаналитический способ. Если требуется выполнить кинематический расчет для некоторого промежутка времени (либо серии положений плоского механизма), то для математического моделирования процесса движения желательно воспользоваться вычислительной техникой.
Графоаналитический способ
Вычертив плоский механизм в заданный момент времени (либо в заданном положении), вычисляют глобальные кинематические характеристики звена (звеньев), которые приводят в движение остальные звенья. Далее, через общие точки звеньев, осуществляется последовательный переход от звена, кинематические характеристики которого известны либо рассчитаны, к другому звену, кинематические характеристики которого возможно рассчитать. Использование векторных зависимостей из лекций 6,7 и 8 требует построения векторных многоугольников (в частном случае – треугольников). Если вычисление неизвестных величин осуществляется с использованием тригонометрии, получаем аналитические зависимости. Если многоугольники построены достаточно корректно, и неизвестные величины могут быть измерены непосредственно на чертеже, тогда возможно их графическое определение. Сказанное и определяет название способа.
ПРИМЕР 31. Для плоского механизма, изображенного на рис.85 в заданном положении (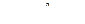 
), рассчитать скорости точек А, В и С, а так же угловую скорость и ускорение звеньев 
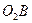и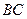 
. Угловую скорость 
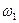и угловое ускорение 
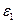звена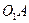 
, а так же длины звеньев и размеры, указанные на рисунке, полагать известными величинами.
1. Зная глобальные кинематические характеристики звена 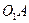, вычислим скорость и составляющие ускорения его точки А:
.
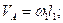
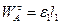Траектория точки А – окружность радиуса .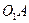
2. Точка А является общей точкой звена 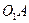и ползуна. Представим движение ползуна по окружности как сложное, состоящее из относительного движения - вдоль звена 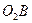, и переносного – вместе с точкой звена 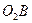, с которой точка А совпадает в данный момент времени (движение по дуге окружности радиуса 
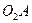). Тогда для скорости точки А можно записать формулу (68):
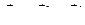. В этом векторном треугольнике известна одна сторона ( 
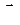) и направления скоростей точки А в относительном (вдоль линии 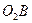) и в переносном (по касательной к окружности радиуса 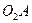) движениях. Построение этого треугольника выполнено на рис.86.
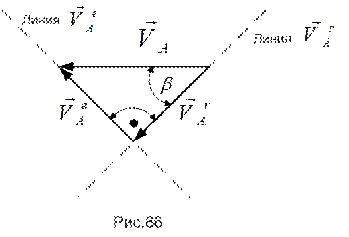
Из построения находим: 
и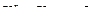 
. Как уже говорилось выше, переносная скорость точки А есть скорость совпадающей с ней точки звена 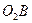. Тогда угловая скорость звена 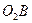будет
.
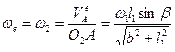Построим для точки А многоугольник ускорений (см. рис.87):
.
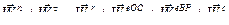Здесь известны оба слагаемых в левой части, можно вычислить в правой част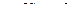и
и 
. Направления векторов ускорений в относительном движении и вращательного в переносном движении совпадают с направлениями скоростей соответствующих движений (см. рис.87).
Из многоугольника имеем: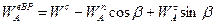 
. Тогда 
.
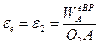Найденные глобальные кинематические характеристики звена 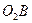позволяют рассчитать скорость и составляющие ускорения точки В:
.
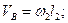
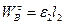Заметим, что совокупность звеньев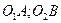 
и ползуна образуют плоский механизм, называемый кривошипно–кулисным.
Совокупность звеньев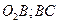 
и ползуна С, как уже говорилось, называется кривошипно-шатунным механизмом.
3. Звено ВС совершает плоское движение. Приняв за полюс точку В, кинематические характеристики которой получены, можно для точки С построить треугольник скоростей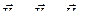 
(см. рис.88) :
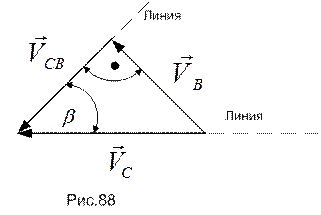
Отсюда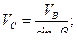 
; 
.
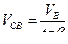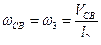Многоугольник ускорений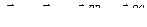 
изображен на рис.89.
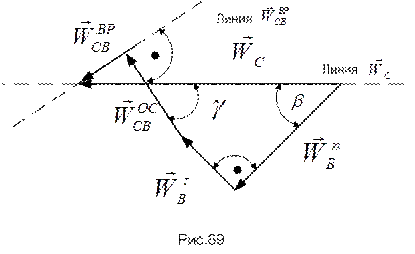
Здесь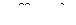 
. Спроецировав многоугольник ускорений на горизонталь и вертикаль, получим систему уравнений для вычисления неизвестных величин 
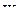и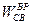 
:
.
Если необходимо найти угловое ускорение движения точки С относительно полюса В, то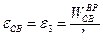 
.
Замечание: получение глобальных кинематических характеристик всех звеньев плоского механизма позволяет рассчитать локальные кинематические характеристики для любой его точки.
Вопросы и задачи для самоконтроля
1. Какой механизм называется плоским?
2. В каком случае удобно использовать графоаналитические методы расчета кинематических характеристик, а в каком – методы расчета на ЭВМ?
3. Какой прием предлагается использовать при решении примера 32 для написания уравнений кинематических связей?
4. Какое соображение позволяет выбирать величину шага численного интегрирования? Каков алгоритм выбора этого шага?
5. Что предлагается сделать, если уравнения кинематических связей не позволяют получить аналитических зависимостей? В чем суть предложенного подхода?
6. В качестве упражнения нарисуйте блок-схему предлагаемого алгоритма расчета.
Список литературы
1. Н.В. Бутенин, Я.Л. Лунц, Д.Р.Меркин., Курс теоретической механики, Т.1, Наука, Москва, 1971г.
2. Мещерский И.В. Задачи по теоретической механике. Лань, Москва, 2002 г.
3. Мелконян А.Л., Теоретическая механика. Статика. Учебное пособие, Издательство СПбГМТУ, СПб, 2009 г.
4. Мелконян А.Л., Черныш А.А. Теоретическая механика. Кинематика. Учебное пособие, Издательство СПбГМТУ, СПб, 2009 г.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Часть 1
КОНСПЕКТ ЛЕКЦИЙ
Утверждено советом университета
В качестве учебного пособия
Санкт-Петербург
2013
ОГЛАВЛЕНИЕ
Лекция 1. Введение. Аксиомы статики. Приведение систем сил к простейшему виду. Условия равновесия
Лекция 2. Принцип освобождения от связей. Типы связей и их реакции. Схема решения задач статики
Лекция 3. Приведение системы параллельных сил к простейшему виду. Центр тяжести твердого тела и способы определения его положения
Лекция 4. Учет трения в задачах статики
Лекция 5. Кинематика т очки
Лекция 6. Простейшие движения твердого тела
Лекция 7. Плоско - параллельное движение твердого тела
Лекция 8. Общий случай движения твердого тела. Сложное движение точки. Сложение скоростей и ускорений
Лекция 9. Кинематика плоских механизмов. Графоаналитический способ. Математическое моделирование процесса движения
10. Список литературы
Лекция 1.
Введение. Аксиомы статики. Приведение систем сил к простейшему виду. Условия равновесия.
Дата: 2019-03-05, просмотров: 395.
