Тепловой шум

Природа теплового шума обусловлена флуктуациями плотности электрического заряда. Проявляется в резисторах. (Рис.23)

Среднее квадратичное значение теплового шума описывается формулой Найквиста:

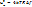,  – постоянная Больцмана,  – температура, К,  – частотный интервал, Гц (Рис. 24)

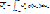
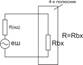
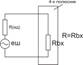
В электрических схемах шум представляется в виде ЭДС или источника тока. При этом сопротивление резистора в такой схеме не обладает шумовыми свойствами. Эквивалентные схемы:

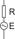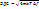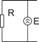
Дробовой шум

Проявляется в p-n переходах полупроводников. Данный вид шума не связан с хаотичным движением электронов, а обусловлен статистическим процессом перехода зарядов из одной области в другую. Иными словами, количество элементарных зарядов, пересекающих p-n переход одинаковый по величине интервал времени, флуктуируют (аналогия с количеством песчинок, перетекающих в песочных часах). В результате, ток через p-n переход будет иметь шумовую компоненту. Среднее квадратичное значение шумового тока описывается формулой Шоттки. 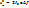,  – среднее значение тока p-n перехода,  – заряд электрона

Эквивалентная схема шумящего диода: (Рис. 27)

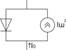
Коэффициент шума.

Шумовые свойства прибора будем характеризовать изменением отношения мощности сигнала к мощности шума между входом и выходом прибора: 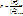 – коэффициент шума. Преобразуем данное выражение. Пусть  –коэффициент усиления по мощности:

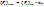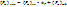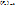; ,  – собственный шум прибора

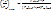, тогда подставляя в выражение 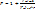. Существенный недостаток данного выражения состоит в том, что значение  зависит от внешнего по отношению к прибору фактора – входного шума 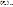. Это делает определение коэффициента шума неоднозначным. Неоднозначность можно преодолеть, если использовать некий стандартный источник внешнего шума. В качестве такого стандартного источника используют тепловой шум резистора, находящегося при температуре T=290К и имеющего сопротивление, равное входному сопротивлению четырёхполюсника. (Рис.27)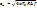

В этом случае мощность шума на входе будет: 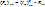 – формула Джоуля-Ленца ¶  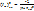– закон Ома

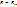 – по условию. В результате подстановок получим: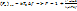

В данную формулу входит только параметр самого прибора. Коэффициент шума и шумовая температура – это два способа характеризации шумовых свойств прибора и между ними существует однозначное соответствие.

Шумовая температура.

Математическую модель шумового прибора можно построить ещё одним способом. В нарисованной выше схеме четырёхполюсника с внешним резистором будем полагать, что прибор является идеальным и нешумящим. При этом собственные шумы прибора учтём, изменив температуру внешнего резистора 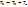, где  и есть шумовая температура прибора. (Рис. 27)

Тогда шумы на выходе можно написать в виде 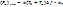. Рассчитаем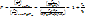

Коэффициент шума и шумовая температура – это два способа характеризации шумовых свойств прибора и между ними существует однозначное соответствие.