Понятие и основные свойства математической модели.
ММ – это эквивалент объекта, выраженный в математической форме.
Построение ММ включает три этапа: Модель->Алгоритм->Программа
Модель – это математическая форма, отражающая важнейшие свойства объекта. По сути, это законы, которым объект подчиняется. Алгоритм – форма реализации модели, которая предполагает последовательность вычисления операций, позволяющих определить искомые величины с необходимой точностью. Программа переводит модель и алгоритм на компьютерный язык.
Основные свойства ММ
1. Множественность и единство модели. Реальный объект имеет несколько неравносильных моделей, отличающихся детализацией свойств объекта. (Рис. 1)
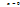 -равновесие. Второй закон Ньютона:
-равновесие. Второй закон Ньютона: 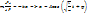 Приведенная модель не учитывает затухания колебаний. С учётом затухания модель имеет вид:
Приведенная модель не учитывает затухания колебаний. С учётом затухания модель имеет вид: 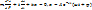
Учёт нелинейности закона Гука тоже может быть детализацией.
2. Универсальность модели заключается в том, что одними и теми же моделями могут описываться совершенно разные по своей природе объекты. 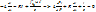 По форме уравнение полностью совпадает с уравнением колебания грузика.
По форме уравнение полностью совпадает с уравнением колебания грузика.
3. Адекватность модели. Это правильное качественное и количественное описание свойств объектов. Например, рассмотренная выше модель колебания грузика без учёта трения адекватна характером колебаний на небольших интервалах времени. Но на больших интервалах, где падение амплитуды значительно, модель без трения неадекватна.
Типы М.М.
1. Структурные и функциональные модели. В структурных моделях отражается структура и взаимосвязь компонентов объекта. Функциональная модель отражает реакцию объекта на внешнее воздействие. Пример, электронная модель проводника – структурная, а вольт-амперная характеристика (закон Ома) – функциональная. Другой пример – полупроводниковый диод. С точки зрения его конструкции p-n перехода и перераспределения зарядов – это структурная модель, а уравнение Шокли, описывающее ВАХ – это функциональная модель.
2. Стационарные и динамические модели. В стационарных моделях свойства модели не меняются во времени. В динамической модели предметом изучения является изменение свойств во времени. Пример, цепь постоянного тока – стационарная модель, пробой диода – динамическая модель.
Применительно к электронным средствам различают также следующие типы моделей: малосигнальные и модели с большим сигналом. Отличие между ними – это учёт нелинейности в зависимости свойств от величины сигнала.
Также различают низкочастотные, высокочастотные и сверхвысокочастотные модели. Пример: резистор на низких и высоких частотах отображается ММ в виде сопротивления (закон Ома).(Рис.3) В диапазоне СВЧ в модель добавляется индуктивный элемент. (Рис.4)
 Рис. 1
Рис. 1
| 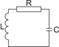 Рис. 2
Рис. 2
|
 Рис. 3
Рис. 3
| 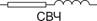 Рис. 4
Рис. 4
|
2.Рабочая точка прибора с нелинейной ВАХ (на примере полупроводникового диода). Методы численного решение нелинейного уравнения.
Уравнение рабочей точки диода (Рис. 5)
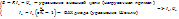 (Рис. 6)
(Рис. 6)
Расчёт параметров рабочей точки можно осуществить аналитически, подставив выражение из первого уравнения для тока во второе. 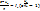 =>
=>  =>
=>  Данное уравнение является нелинейным относительно
Данное уравнение является нелинейным относительно  и не может быть решено аналитически. Рассмотрим численный метод решения нелинейных уравнений вида
и не может быть решено аналитически. Рассмотрим численный метод решения нелинейных уравнений вида 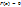 .
.
1. Метод последовательных приближений.
В этом методе преобразуем исходное уравнение к виду 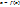 ,
, 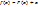
Выберем приближённое значение  , являющееся близким к решению (например, на основе графического расчёта). Тогда первое приближение рассчитывается по формуле
, являющееся близким к решению (например, на основе графического расчёта). Тогда первое приближение рассчитывается по формуле 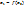 , второе
, второе 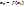 , n-ое
, n-ое 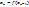
Последовательность  в качестве предела имеет точное значение для решения искомого уравнения
в качестве предела имеет точное значение для решения искомого уравнения 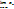 =
= 
(Рис. 7) (Рис. 8) Условием сходимости метода будет 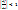 . Процесс расчёта численного решения с заданной точностью
. Процесс расчёта численного решения с заданной точностью  заканчивается при выполнении условия
заканчивается при выполнении условия 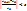 – относительная погрешность
– относительная погрешность
2. Метод касательной (метод Ньютона-Рафсона).
Исходное уравнение 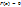 . В этом методе функция представляется в окрестности искомой точки в виде:
. В этом методе функция представляется в окрестности искомой точки в виде: 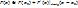 . Первое приближение
. Первое приближение 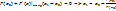 . Следующие шаги в приближении к решению строятся на основании формулы
. Следующие шаги в приближении к решению строятся на основании формулы 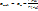 . По сути метод основан на замене функции
. По сути метод основан на замене функции 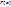 её касательной в выбранной точке
её касательной в выбранной точке  (Рис. 9)
(Рис. 9)
3. Метод половинного деления.
Исходное уравнение 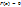 . Выберем отрезок, внутри которого функция меняет знак. Такой выбор отрезка эквивалентен утверждению, что внутри него
. Выберем отрезок, внутри которого функция меняет знак. Такой выбор отрезка эквивалентен утверждению, что внутри него 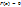 . Делим отрезок пополам и выбираем ту половину, внутри которой
. Делим отрезок пополам и выбираем ту половину, внутри которой 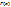 по-прежнему меняет знак, то есть для новых значений
по-прежнему меняет знак, то есть для новых значений 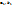
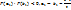 , ещё раз делим пополам и выбираем ту половину, в которой
, ещё раз делим пополам и выбираем ту половину, в которой 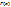 меняет знак. В результате n шагов расчёта исходный отрезок сузится до интервала
меняет знак. В результате n шагов расчёта исходный отрезок сузится до интервала 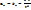 . Если необходима точность расчёта эпсилон, то количество шагов n определяется неравенством
. Если необходима точность расчёта эпсилон, то количество шагов n определяется неравенством 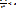 (абсолютная погрешность). Неравенство позволяет прогнозировать количество шагов, необходимых для расчёта.
(абсолютная погрешность). Неравенство позволяет прогнозировать количество шагов, необходимых для расчёта.
4. Метод хорд.
Исходное уравнение 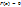 . Как и в методе половинных разбиений выбираем отрезок, на концах которого значения
. Как и в методе половинных разбиений выбираем отрезок, на концах которого значения 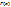 имеют разный знак. При этом внутри отрезка функцию
имеют разный знак. При этом внутри отрезка функцию 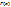 заменяем хордой (см. рис ниже). Хорда делит отрезок на две части, выбираем ту часть, внутри которой
заменяем хордой (см. рис ниже). Хорда делит отрезок на две части, выбираем ту часть, внутри которой 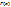 по-прежнему меняет знак. В этом новом отрезке опять проводим хорду и т.д.
по-прежнему меняет знак. В этом новом отрезке опять проводим хорду и т.д.
(Рис.10). Если в методе касательных исходная функция 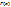 представлялась в виде прямой, касающейся зависимости
представлялась в виде прямой, касающейся зависимости 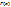 в выбранной точке, то в методе хорд
в выбранной точке, то в методе хорд 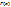 представляется в виде прямой, соединяющей точки, через который проходит функция на концах отрезка [a;b]. Иными словами, осуществляется замена
представляется в виде прямой, соединяющей точки, через который проходит функция на концах отрезка [a;b]. Иными словами, осуществляется замена 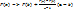 – уравнение хорды. Тогда в первом приближении определяем значение
– уравнение хорды. Тогда в первом приближении определяем значение  по уравнению
по уравнению 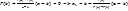 . Из отрезков
. Из отрезков 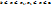 выбираем тот, для которого выполняется неравенство
выбираем тот, для которого выполняется неравенство 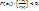
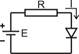 Рис. 5
Рис. 5
|  Рис. 6
Рис. 6
| 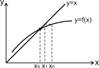 Рис. 7
Рис. 7
|
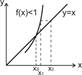 Рис8
Рис8
|  Рис. 9
Рис. 9
| 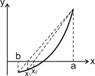 Рис. 10
Рис. 10
|
Метод конечных элементов.
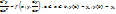
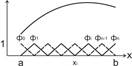
В основе метода лежит представление искомой функции y(x) по базисным функциям 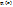 со следующими особенностями этих базисных функций:
со следующими особенностями этих базисных функций:
1. 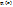 – линейная функция на каждом отрезке
– линейная функция на каждом отрезке 
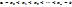 ¶
¶ 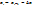
2. 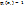 и
и 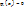 j≠i (Рис.19)
j≠i (Рис.19)
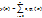
Исходя из свойств базисной функции, заключаем, что 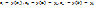 – из граничных условий
– из граничных условий
Таким образом, расчет коэффициентов  дает набор значений функции y(x) в дискретном наборе значений x (
дает набор значений функции y(x) в дискретном наборе значений x ( 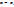 ) (На рисунке эти значения обозначены жирным точками). С одной стороны метод имеет сходство с проекционным методом (методом Галёркина) – используется разложение по базисным функциям. С другой стороны в результате расчет получается набор дискретных значений
) (На рисунке эти значения обозначены жирным точками). С одной стороны метод имеет сходство с проекционным методом (методом Галёркина) – используется разложение по базисным функциям. С другой стороны в результате расчет получается набор дискретных значений 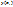 – как в методах Эйлера и Рунге-Кутта. Как и в методе Галеркина,
– как в методах Эйлера и Рунге-Кутта. Как и в методе Галеркина,  находится минимизацией невязки:
находится минимизацией невязки:
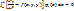 ;
; 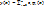 Для всех
Для всех 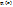 с i=1,…,n-1 (Напомним что
с i=1,…,n-1 (Напомним что  )
)
Для использования в расчетах проинтегрируем выражение со второй производной. Интегрируем по частям.
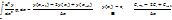
Таким образом, условия невязки можно представить в виде 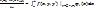
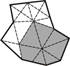
В этом случае рассматриваемая двухмерная поверхность разбивается с помощью сетки на треугольники (триагуляция). К вершинам сетки привязаны базисные функции  со следующими свойствами:
со следующими свойствами:
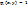 ,
, 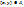 – вершина «шатра» ¶
– вершина «шатра» ¶ 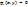 для остальных вершин ¶
для остальных вершин ¶  линейная функция по “x” и “y”
линейная функция по “x” и “y”
(Рис. 20)
| 
|
Метод наименьших квадратов.
При снятии ВАХ резистора экспериментальным способом множество полученных точек должны быть связаны между собой зависимостью U=RI – закон Ома. Как по экспериментальным значениям провести наилучшую линию и определить наилучшие значения сопротивления  ? (Рис. 22)
? (Рис. 22)
Математическая постановка задачи: пусть требуется найти зависимость общего вида, связывающую экспериментальные значения  и
и  ,
, 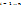 ;
; 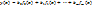
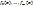 – известные функции;
– известные функции; 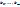 – коэффициенты, которые нужно найти
– коэффициенты, которые нужно найти
Критерием наилучших значений коэффициентов  является минимизация следующей суммы
является минимизация следующей суммы 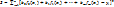
Рассматривая S как функцию переменных 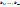 напишем условие достижения минимума в виде уравнения
напишем условие достижения минимума в виде уравнения 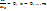 Выполняя дифференцирование, получим следующую структуру уравнений:
Выполняя дифференцирование, получим следующую структуру уравнений: 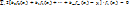 Вынося
Вынося 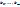 за знак сумм, получим окончательно:
за знак сумм, получим окончательно: 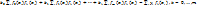
Отсюда видно, что получается система линейных уравнений относительно b.

Коэффициент шума.
Шумовые свойства прибора будем характеризовать изменением отношения мощности сигнала к мощности шума между входом и выходом прибора: 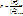 – коэффициент шума. Преобразуем данное выражение. Пусть
– коэффициент шума. Преобразуем данное выражение. Пусть  –коэффициент усиления по мощности:
–коэффициент усиления по мощности:
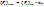 ;
; 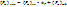 ,
, 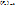 – собственный шум прибора
– собственный шум прибора
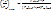 , тогда подставляя в выражение
, тогда подставляя в выражение 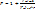 . Существенный недостаток данного выражения состоит в том, что значение
. Существенный недостаток данного выражения состоит в том, что значение  зависит от внешнего по отношению к прибору фактора – входного шума
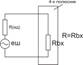
зависит от внешнего по отношению к прибору фактора – входного шума 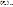 . Это делает определение коэффициента шума неоднозначным. Неоднозначность можно преодолеть, если использовать некий стандартный источник внешнего шума. В качестве такого стандартного источника используют тепловой шум резистора, находящегося при температуре T=290К и имеющего сопротивление, равное входному сопротивлению четырёхполюсника. (Рис.27)
. Это делает определение коэффициента шума неоднозначным. Неоднозначность можно преодолеть, если использовать некий стандартный источник внешнего шума. В качестве такого стандартного источника используют тепловой шум резистора, находящегося при температуре T=290К и имеющего сопротивление, равное входному сопротивлению четырёхполюсника. (Рис.27) 
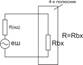
В этом случае мощность шума на входе будет: 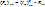 – формула Джоуля-Ленца ¶
– формула Джоуля-Ленца ¶ 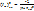 – закон Ома
– закон Ома
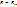 – по условию. В результате подстановок получим:
– по условию. В результате подстановок получим: 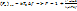
В данную формулу входит только параметр самого прибора. Коэффициент шума и шумовая температура – это два способа характеризации шумовых свойств прибора и между ними существует однозначное соответствие.
Шумовая температура.
Математическую модель шумового прибора можно построить ещё одним способом. В нарисованной выше схеме четырёхполюсника с внешним резистором будем полагать, что прибор является идеальным и нешумящим. При этом собственные шумы прибора учтём, изменив температуру внешнего резистора 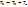 , где
, где  и есть шумовая температура прибора. (Рис. 27)
и есть шумовая температура прибора. (Рис. 27)
Тогда шумы на выходе можно написать в виде 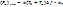 . Рассчитаем
. Рассчитаем 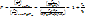
Коэффициент шума и шумовая температура – это два способа характеризации шумовых свойств прибора и между ними существует однозначное соответствие.
Понятие и основные свойства математической модели.
ММ – это эквивалент объекта, выраженный в математической форме.
Построение ММ включает три этапа: Модель->Алгоритм->Программа
Модель – это математическая форма, отражающая важнейшие свойства объекта. По сути, это законы, которым объект подчиняется. Алгоритм – форма реализации модели, которая предполагает последовательность вычисления операций, позволяющих определить искомые величины с необходимой точностью. Программа переводит модель и алгоритм на компьютерный язык.
Основные свойства ММ
1. Множественность и единство модели. Реальный объект имеет несколько неравносильных моделей, отличающихся детализацией свойств объекта. (Рис. 1)
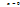 -равновесие. Второй закон Ньютона:
-равновесие. Второй закон Ньютона: 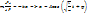 Приведенная модель не учитывает затухания колебаний. С учётом затухания модель имеет вид:
Приведенная модель не учитывает затухания колебаний. С учётом затухания модель имеет вид: 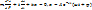
Учёт нелинейности закона Гука тоже может быть детализацией.
2. Универсальность модели заключается в том, что одними и теми же моделями могут описываться совершенно разные по своей природе объекты. 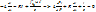 По форме уравнение полностью совпадает с уравнением колебания грузика.
По форме уравнение полностью совпадает с уравнением колебания грузика.
3. Адекватность модели. Это правильное качественное и количественное описание свойств объектов. Например, рассмотренная выше модель колебания грузика без учёта трения адекватна характером колебаний на небольших интервалах времени. Но на больших интервалах, где падение амплитуды значительно, модель без трения неадекватна.
Типы М.М.
1. Структурные и функциональные модели. В структурных моделях отражается структура и взаимосвязь компонентов объекта. Функциональная модель отражает реакцию объекта на внешнее воздействие. Пример, электронная модель проводника – структурная, а вольт-амперная характеристика (закон Ома) – функциональная. Другой пример – полупроводниковый диод. С точки зрения его конструкции p-n перехода и перераспределения зарядов – это структурная модель, а уравнение Шокли, описывающее ВАХ – это функциональная модель.
2. Стационарные и динамические модели. В стационарных моделях свойства модели не меняются во времени. В динамической модели предметом изучения является изменение свойств во времени. Пример, цепь постоянного тока – стационарная модель, пробой диода – динамическая модель.
Применительно к электронным средствам различают также следующие типы моделей: малосигнальные и модели с большим сигналом. Отличие между ними – это учёт нелинейности в зависимости свойств от величины сигнала.
Также различают низкочастотные, высокочастотные и сверхвысокочастотные модели. Пример: резистор на низких и высоких частотах отображается ММ в виде сопротивления (закон Ома).(Рис.3) В диапазоне СВЧ в модель добавляется индуктивный элемент. (Рис.4)
 Рис. 1
Рис. 1
|  Рис. 2
Рис. 2
|
 Рис. 3
Рис. 3
| 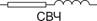 Рис. 4
Рис. 4
|
2.Рабочая точка прибора с нелинейной ВАХ (на примере полупроводникового диода). Методы численного решение нелинейного уравнения.
Уравнение рабочей точки диода (Рис. 5)
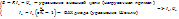 (Рис. 6)
(Рис. 6)
Расчёт параметров рабочей точки можно осуществить аналитически, подставив выражение из первого уравнения для тока во второе. 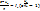 =>
=>  =>
=>  Данное уравнение является нелинейным относительно
Данное уравнение является нелинейным относительно  и не может быть решено аналитически. Рассмотрим численный метод решения нелинейных уравнений вида
и не может быть решено аналитически. Рассмотрим численный метод решения нелинейных уравнений вида 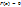 .
.
1. Метод последовательных приближений.
В этом методе преобразуем исходное уравнение к виду 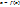 ,
, 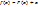
Выберем приближённое значение  , являющееся близким к решению (например, на основе графического расчёта). Тогда первое приближение рассчитывается по формуле
, являющееся близким к решению (например, на основе графического расчёта). Тогда первое приближение рассчитывается по формуле 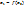 , второе
, второе 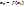 , n-ое
, n-ое 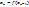
Последовательность  в качестве предела имеет точное значение для решения искомого уравнения
в качестве предела имеет точное значение для решения искомого уравнения 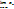 =
= 
(Рис. 7) (Рис. 8) Условием сходимости метода будет 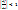 . Процесс расчёта численного решения с заданной точностью
. Процесс расчёта численного решения с заданной точностью  заканчивается при выполнении условия
заканчивается при выполнении условия 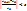 – относительная погрешность
– относительная погрешность
2. Метод касательной (метод Ньютона-Рафсона).
Исходное уравнение 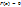 . В этом методе функция представляется в окрестности искомой точки в виде:
. В этом методе функция представляется в окрестности искомой точки в виде: 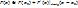 . Первое приближение
. Первое приближение 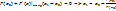 . Следующие шаги в приближении к решению строятся на основании формулы
. Следующие шаги в приближении к решению строятся на основании формулы 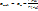 . По сути метод основан на замене функции
. По сути метод основан на замене функции 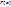 её касательной в выбранной точке
её касательной в выбранной точке  (Рис. 9)
(Рис. 9)
3. Метод половинного деления.
Исходное уравнение 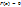 . Выберем отрезок, внутри которого функция меняет знак. Такой выбор отрезка эквивалентен утверждению, что внутри него
. Выберем отрезок, внутри которого функция меняет знак. Такой выбор отрезка эквивалентен утверждению, что внутри него 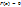 . Делим отрезок пополам и выбираем ту половину, внутри которой
. Делим отрезок пополам и выбираем ту половину, внутри которой 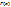 по-прежнему меняет знак, то есть для новых значений
по-прежнему меняет знак, то есть для новых значений 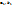
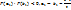 , ещё раз делим пополам и выбираем ту половину, в которой
, ещё раз делим пополам и выбираем ту половину, в которой 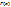 меняет знак. В результате n шагов расчёта исходный отрезок сузится до интервала
меняет знак. В результате n шагов расчёта исходный отрезок сузится до интервала 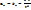 . Если необходима точность расчёта эпсилон, то количество шагов n определяется неравенством
. Если необходима точность расчёта эпсилон, то количество шагов n определяется неравенством 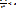 (абсолютная погрешность). Неравенство позволяет прогнозировать количество шагов, необходимых для расчёта.
(абсолютная погрешность). Неравенство позволяет прогнозировать количество шагов, необходимых для расчёта.
4. Метод хорд.
Исходное уравнение 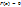 . Как и в методе половинных разбиений выбираем отрезок, на концах которого значения
. Как и в методе половинных разбиений выбираем отрезок, на концах которого значения 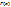 имеют разный знак. При этом внутри отрезка функцию
имеют разный знак. При этом внутри отрезка функцию 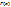 заменяем хордой (см. рис ниже). Хорда делит отрезок на две части, выбираем ту часть, внутри которой
заменяем хордой (см. рис ниже). Хорда делит отрезок на две части, выбираем ту часть, внутри которой 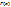 по-прежнему меняет знак. В этом новом отрезке опять проводим хорду и т.д.
по-прежнему меняет знак. В этом новом отрезке опять проводим хорду и т.д.
(Рис.10). Если в методе касательных исходная функция 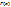 представлялась в виде прямой, касающейся зависимости
представлялась в виде прямой, касающейся зависимости 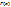 в выбранной точке, то в методе хорд
в выбранной точке, то в методе хорд 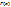 представляется в виде прямой, соединяющей точки, через который проходит функция на концах отрезка [a;b]. Иными словами, осуществляется замена
представляется в виде прямой, соединяющей точки, через который проходит функция на концах отрезка [a;b]. Иными словами, осуществляется замена 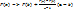 – уравнение хорды. Тогда в первом приближении определяем значение
– уравнение хорды. Тогда в первом приближении определяем значение  по уравнению
по уравнению 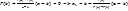 . Из отрезков
. Из отрезков 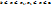 выбираем тот, для которого выполняется неравенство
выбираем тот, для которого выполняется неравенство 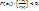
 Рис. 5
Рис. 5
|  Рис. 6
Рис. 6
|  Рис. 7
Рис. 7
|
 Рис8
Рис8
|  Рис. 9
Рис. 9
|  Рис. 10
Рис. 10
|
Дата: 2019-03-05, просмотров: 319.