Метод Эйлера с пересчётом (модифицированный метод)

В этом методе значение 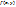 берётся как среднее между значением в начале отрезка и прогнозируемым значением в конце его, т.е. на каждом отрезке  прогнозируется значение  в конце отрезка: 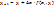 – прогноз (предиктор). Тогда: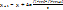

В результате может быть построена зависимость с более близкими значениями к точной зависимости , чем в явном или неявном методе.

Метод Рунге-Кутта

Идея замены 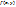 средним значением получила распространение в методе Рунге-Кутта. В этом случае берётся среднее от шести значений 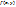. При этом: 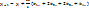, где:

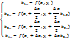
Метод имеет точность 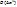 в отличие от метода Эйлера - .

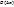9.Проекционный метод решения м.у. (метод Галеркина).

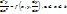
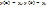
Решение в методе Галёркина ищется в виде линейной комбинации базисных функций 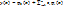, где 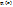 – линейно независимая функция, обладающая свойством полноты и удовлетворяющие следующим граничным условиям: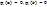

При этом за выполнение граничных условий для искомой функции y(x) отвечает функция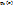  
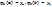. Как правило, функции  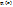выбирают в виде  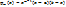или 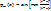 Далее расчёт строится таким образом, чтобы найти наилучшие значения коэффициентов . Если в исходное дифференциальное уравнение подставить функцию в виде представленного разложения, то левые и правые части не совпадут друг с другом. Разница между левой и правой частью образует функцию, которую называют невязкой: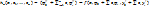

В методе Галёркина коэффициенты  определяются на основе n уравнений 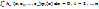Интеграл трактуется как проекция невязки на базисные функции, а сами уравнений, определяющие n коэффициенты трактуются как условия ортогональности невязки к первым n функциям базиса.

Метод конечных элементов.

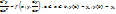
В основе метода лежит представление искомой функции y(x) по базисным функциям 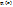 со следующими особенностями этих базисных функций:

1. 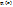 – линейная функция на каждом отрезке  ¶  

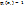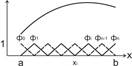
2.  и 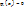 j≠i (Рис.19)

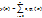
Исходя из свойств базисной функции, заключаем, что 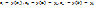 – из граничных условий

Таким образом, расчет коэффициентов  дает набор значений функции y(x) в дискретном наборе значений x ( 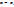) (На рисунке эти значения обозначены жирным точками). С одной стороны метод имеет сходство с проекционным методом (методом Галёркина) – используется разложение по базисным функциям. С другой стороны в результате расчет получается набор дискретных значений  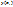– как в методах Эйлера и Рунге-Кутта. Как и в методе Галеркина,  находится минимизацией невязки:

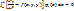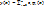; Для всех  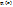с i=1,…,n-1 (Напомним что )

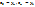Для использования в расчетах проинтегрируем выражение со второй производной. Интегрируем по частям.

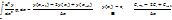
Таким образом, условия невязки можно представить в виде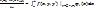

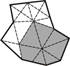
В этом случае рассматриваемая двухмерная поверхность разбивается с помощью сетки на треугольники (триагуляция). К вершинам сетки привязаны базисные функции  со следующими свойствами:

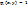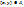,  – вершина «шатра» ¶  для остальных вершин ¶  линейная функция по “x” и “y”

(Рис. 20)