Явный метод Эйлера: 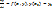
На малом отрезке  представим производную в виде конечно-разностного отношения. Тогда
представим производную в виде конечно-разностного отношения. Тогда 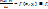
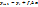 ; Данное соотношение позволяет выразить значение y в конце отрезка
; Данное соотношение позволяет выразить значение y в конце отрезка  через значение в начале отрезка. В частности,
через значение в начале отрезка. В частности,  и т.д. (Рис.16)
и т.д. (Рис.16)
Основной вопрос, который возникает при построении приближенного решения следующий: будет ли приближенная зависимость стремиться к точной, если 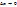 . Исследуем данный вопрос на частном примере – расчёте переходной характеристики RC-цепи. (Рис.17)
. Исследуем данный вопрос на частном примере – расчёте переходной характеристики RC-цепи. (Рис.17) 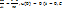 разряжен
разряжен  ¶
¶
Явный метод Эйлера: 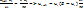 (Рис. 18)
(Рис. 18)
Кстати, рассчитав отдельные дискретные значения, можно построить непрерывную интерполяционную зависимость. Выясним вопрос об устойчивости метода, а именно: если начальное условие будет 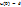 , то будет ли при этом выполняться неравенство
, то будет ли при этом выполняться неравенство  – конечное число при любом
– конечное число при любом  . Выбор погрешности
. Выбор погрешности  при
при 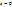 в начальный момент совсем необязателен (не имеет принципиального значения для последующих рассуждений).
в начальный момент совсем необязателен (не имеет принципиального значения для последующих рассуждений).  может быть например, погрешностью округления до какого-то знака какого-то промежуточного значения
может быть например, погрешностью округления до какого-то знака какого-то промежуточного значения  . Введём для удобства новые параметры:
. Введём для удобства новые параметры: 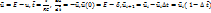 В данных обозначениях соседние значения искомой функции связаны множителем
В данных обозначениях соседние значения искомой функции связаны множителем 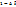 , поэтому продолжив равенство, получим окончательно
, поэтому продолжив равенство, получим окончательно 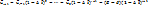 . Сравним значения с
. Сравним значения с 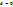 и
и 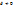 :
: 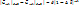 . Если
. Если 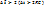 , то
, то 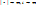
Из проведенного анализа следует, что от выбранного шага разбиения времени на интервалы  будет зависеть сходимость приближённого решения к асимптотическому значению
будет зависеть сходимость приближённого решения к асимптотическому значению  : если
: если 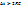 , построенное по методу Эйлера решение не только не стремится к значению
, построенное по методу Эйлера решение не только не стремится к значению  , а вообще не стремится к какому-то конечному значению (верхняя зависимость на рисунке). Асимптотическое приближение к
, а вообще не стремится к какому-то конечному значению (верхняя зависимость на рисунке). Асимптотическое приближение к  будет только при выборе
будет только при выборе 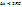 . В этом случае говорят, что метод неустойчив при
. В этом случае говорят, что метод неустойчив при 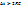 и устойчив при
и устойчив при 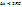 . Накапливающаяся ошибка при большом шаге разбиения связана с тем, что производная на этом шаге существенно меняется и замена её конечно-разностным отношением недопустима.
. Накапливающаяся ошибка при большом шаге разбиения связана с тем, что производная на этом шаге существенно меняется и замена её конечно-разностным отношением недопустима.
Неявный метод Эйлера
В данном случае производная по-прежнему аппроксимируется конечно-разностным отношением, однако 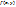 берется не в начале, а в конце интервала разбиения, т.е.
берется не в начале, а в конце интервала разбиения, т.е. 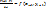 . Поскольку
. Поскольку  содержится в обеих частях уравнения, то чтобы его найти, нужно решить данное уравнение. Иными словами
содержится в обеих частях уравнения, то чтобы его найти, нужно решить данное уравнение. Иными словами  связан с
связан с  неявно. Проведём исследование устойчивости данного метода также на примере RC-цепи.
неявно. Проведём исследование устойчивости данного метода также на примере RC-цепи.
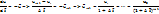
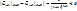 – метод устойчив при любом
– метод устойчив при любом 
Таким образом, неявный метод более устойчив по сравнению с явным. Причем данное свойство присуще не только конкретному примеру, но и наиболее общему случаю (произвольные функции  ).
).
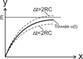 Рис. 16
Рис. 16
| 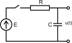 Рис. 17
Рис. 17
| 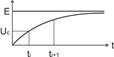 Рис.18
Рис.18
|
Дата: 2019-03-05, просмотров: 298.