Рассмотрим уравнение с частными производными, например уравнение теплопроводности (или диффузии)

; ¶

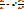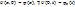
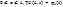
Используя аппроксимацию заменим производную 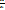 конечно-разностным отношением: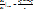  

В итоге заменяем исходное дифференциальное уравнение конечно разностным алгебраическим уравнением:

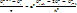
Нарисовать шаблон. Рассмотренная схема называлась явной разностной схемой. Возможны и другие схемы, например неявная. Для неё аппроксимирующее выражение второй для производной в исходном уравнении рассматривается не в n-слое, а в n+1. Тогда разностная схема приобретает вид:

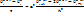
Нарисовать шаблон. Сложив уравнения явной и неявной разностной схем и разделив пополам, получим ещё одну разностную схему, известную как схема Кранка-Николсона:

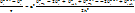
Нарисовать шаблон.

13.Устойчивость разностных схем. Исследование устойчивости методом Фурье (на примере явной и неявной схем уравнения теплопроводности).

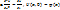 – начальные условия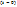

Если изменить начальные условия 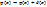, причем  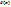имеет маленькие значения, будет ли новое решение близким к старому?

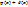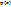Уравнение теплопроводности является линейным и значит, любая линейная комбинация его решения тоже является решением. В частности, решением будет разница решений с начальным условием  и . Очевидно, что для этой разности начальные условия формулируются как  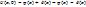. Теперь полагая, что  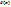– функция с маленькими значениями, естественно предположить что  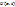тоже будет иметь маленькие значения. Математически, условие устойчивости выражается в виде неравенства:

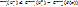 (*) , причём С не зависит от  и  (шагов сетки). Если решение дифференциального уравнения существует, а разностная схема аппроксимирующего уравнения устойчива, то разностное решение сходится к точному.

Метод Фурье. Идея метода заключается в проверке неравенства (*), в котором в качестве начального условия (функция 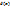) выбирается гармоническая функция ( 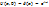, k – целое число. В самом деле, любое начальное условие можно представить в виде ряда Фурье

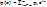, k – коэффициент ряда; и тогда убедившись в устойчивости разностной схемы для любой гармоники этого ряда, можно быть уверенным, что разностная схема устойчива.

Рассмотрим пример: 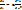 явная разностная схема ;

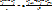Начальные условия (во временном слое t=0: 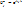) ¶В методе Фурье решение в n-ом временном слое ищется в виде:

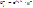 ¶Выпишем выражение для слагаемых разностной схемы: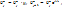

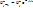
Подставляя в уравнение разностной схемы и сокращая , получим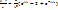

Воспользуемся формулой Эйлера:

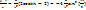
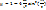
Отсюда следует, что 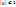, если  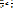(для любого k)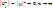

В частности, 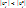, т.е. неравенство (*) выполнено и схема устойчива. Однако, если 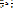, то для тех значений k, для которых  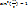будет 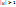 и разностная схема неустойчива Вывод: явная разностная схема условно устойчива, если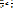

Устойчивость неявной разностной схемы.

Как и в явной схеме, ищем решение в виде: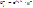

Как и прежде, выражаем все остальные слагаемые через данное слагаемое: , ,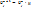

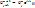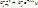
Подставляя в разностное уравнение, выполняя сокращения и алгебраические преобразования, получим:

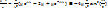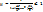,  для всех k

Поскольку временная зависимость (n-ый временной слой) узловых значений функции 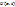 определяется множителем , то 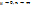 при всех  И тогда требование устойчивости (неравенство *) выполнено, а неявная разностная схема абсолютно устойчива.

Метод наименьших квадратов.

При снятии ВАХ резистора экспериментальным способом множество полученных точек должны быть связаны между собой зависимостью U=RI – закон Ома. Как по экспериментальным значениям провести наилучшую линию и определить наилучшие значения сопротивления 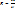? (Рис. 22)

Математическая постановка задачи: пусть требуется найти зависимость общего вида, связывающую экспериментальные значения  и , ;

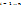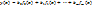
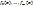 – известные функции;  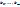– коэффициенты, которые нужно найти

Критерием наилучших значений коэффициентов  является минимизация следующей суммы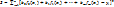

Рассматривая S как функцию переменных 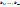 напишем условие достижения минимума в виде уравнения 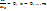Выполняя дифференцирование, получим следующую структуру уравнений: 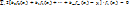Вынося  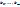за знак сумм, получим окончательно: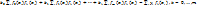

Отсюда видно, что получается система линейных уравнений относительно b.