Припустимо (для спрощення позначень), що у матриці 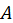 кількість рядків не менша, ніж кількість стовпців, тобто
кількість рядків не менша, ніж кількість стовпців, тобто 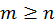 . Це означає, що є
. Це означає, що є 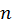 сингулярних чисел
сингулярних чисел 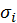 ,
, 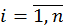 .
.
Алгоритм ділиться на два етапи.
Перший етап - приведення матриці 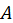 до двохдіагональної форми, в якій ненульовими можуть бути лише елементи діагоналі і першої наддіагоналі.
до двохдіагональної форми, в якій ненульовими можуть бути лише елементи діагоналі і першої наддіагоналі.
Другий етап - ітераційний процес, в якому наддіагональні елементи зменшуються до малої величини, що дає бажану діагональну форму.
Перший етап здійснюється за допомогою перетворення, яке називається хаусхолдеровим відбиттям. Для розуміння суті цього перетворення розглянемо його геометричну інтерпретацію. Зробимо в 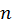 - вимірному векторному просторі відображення відносно деякої гіперплощини, що проходить через початок координат. Гіперплощина (і, отже, перетворення) визначається завданням нормалі
- вимірному векторному просторі відображення відносно деякої гіперплощини, що проходить через початок координат. Гіперплощина (і, отже, перетворення) визначається завданням нормалі 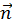 до цієї гіперплощини. Нехай вектор
до цієї гіперплощини. Нехай вектор 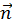 є нормованим, тобто
є нормованим, тобто 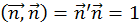 .
.
Розкладемо довільний вектор 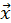 на дві складові: одну - паралельно нормалі (тобто
на дві складові: одну - паралельно нормалі (тобто 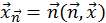 ), другу - перпендикулярно до неї. При відображенні вектору відносно гіперплощини перпендикулярна складова залишається незмінною, а паралельна міняє знак (рис. 6). Відбитий вектор
), другу - перпендикулярно до неї. При відображенні вектору відносно гіперплощини перпендикулярна складова залишається незмінною, а паралельна міняє знак (рис. 6). Відбитий вектор 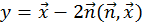 ) відрізняється від початкового на подвоєну величину паралельної складової.
) відрізняється від початкового на подвоєну величину паралельної складової.
| Рисунок 6 – Хаусхолдерове відбиття |
| 0 |
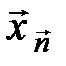
|
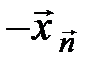
|
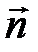
|
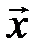
|
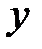
|
Це перетворення вектора 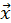 можна записати в канонічній формі
можна записати в канонічній формі
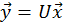 , де
, де 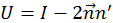 .
.
Матриця 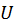 називається хаусхолдеровим відбиттям.
називається хаусхолдеровим відбиттям.
Тепер візьмемо в якості 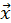 перший стовпець
перший стовпець 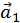 матриці
матриці 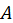 , а в якості
, а в якості 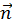 - вектор
- вектор 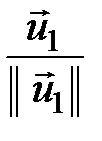 , де
, де
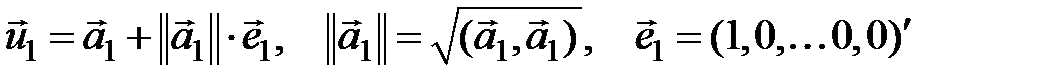 .
.
Тоді
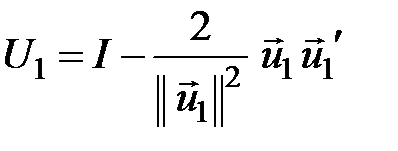
та
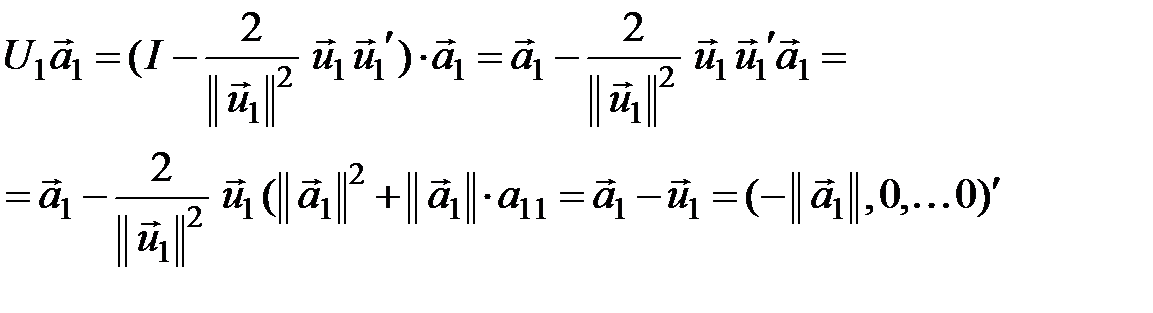
(  - перша координата вектора
- перша координата вектора  ).
).
У перетвореннях Хаусхолдера гіперплощина, відносно якої відбувається відбиття, вибирається так, що вектор 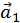 відображається у вектор, у якого відмінна від нуля тільки перша координата. Гіперплощина визначається завданням вектору нормалі до неї. Тому вибір гіперплощини - це, кінець кінцем, вибір вектору нормалі. У нашому випадку нормаль
відображається у вектор, у якого відмінна від нуля тільки перша координата. Гіперплощина визначається завданням вектору нормалі до неї. Тому вибір гіперплощини - це, кінець кінцем, вибір вектору нормалі. У нашому випадку нормаль
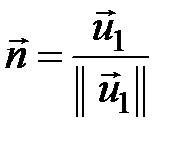
будується за допомогою вектору, який відбивається, а саме 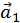 , в результаті отримуємо бажані нулі у векторі
, в результаті отримуємо бажані нулі у векторі 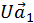 .
.
Таким чином, за першим вектор-стовпцем 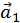 матриці
матриці 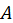 будується вектор
будується вектор 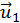 , який відрізняється від вектору
, який відрізняється від вектору 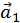 тільки першою координатою: вона збільшена на
тільки першою координатою: вона збільшена на 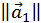 (евклідова норма). Потім визначаємо
(евклідова норма). Потім визначаємо 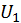 і з допомогою
і з допомогою 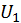 перетворюємо матрицю
перетворюємо матрицю 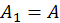 . Матрицю
. Матрицю 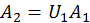 знаходимо стовпець за стовпцем.
знаходимо стовпець за стовпцем.
Ортогональність 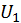 дуже важлива. З неї витікає, що довжина кожного стовпця в
дуже важлива. З неї витікає, що довжина кожного стовпця в 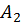 дорівнює довжині відповідного стовпця в
дорівнює довжині відповідного стовпця в 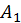 , тобто ортогональні перетворення не збільшують помилок.
, тобто ортогональні перетворення не збільшують помилок.
Перш ніж вводити нулі в другому стовпці під діагоналлю, отримують нулі в першому рядку за допомогою перетворення 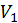 . При цьому нулі, вже отримані в першому стовпці, мають бути збережені, а довжина першого рядка не повинна змінитися. На цьому кроці для матриці порядку
. При цьому нулі, вже отримані в першому стовпці, мають бути збережені, а довжина першого рядка не повинна змінитися. На цьому кроці для матриці порядку 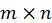 повинно бути отримано
повинно бути отримано 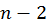 нуля.
нуля.
Перетворення 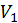 є також перетворенням відбиття і породжується першим рядком матриці
є також перетворенням відбиття і породжується першим рядком матриці 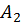 . Спочатку будується вектор
. Спочатку будується вектор 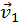 , усі координати якого, окрім першої і другої, дорівнюють відповідним елементам першого рядка
, усі координати якого, окрім першої і другої, дорівнюють відповідним елементам першого рядка 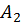 . Його перша координата дорівнює нулю, а друга дорівнює другому елементу першого рядка
. Його перша координата дорівнює нулю, а друга дорівнює другому елементу першого рядка 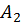 , зменшеному на норму вектору (розмірності
, зменшеному на норму вектору (розмірності 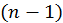 ),
),
координати якого - елементи першого рядка 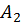 , починаючи з другого елемента, в природному їх порядку.
, починаючи з другого елемента, в природному їх порядку.
Далі обчислюємо
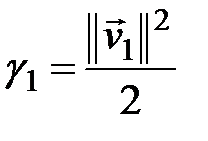
і визначаємо перетворення 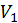 за формулою
за формулою
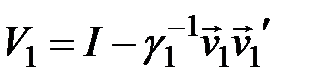 .
.
З допомогою 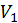 перетворюємо
перетворюємо 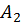 і отримуємо
і отримуємо 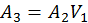 .
.
Матриця 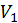 є ортогональною.
є ортогональною.
Далі вводяться нулі в другий стовпець під діагоналлю, причому нулі, отримані раніше, зберігаються. Для цього потрібно перейти в 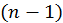 - вимірний підпростір з нульовою першою координатою. Будується вектор
- вимірний підпростір з нульовою першою координатою. Будується вектор 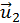 , координати якого, починаючи з третьої, дорівнюють відповідним елементам другого стовпця, перша координата дорівнює нулю, а друга дорівнює другому елементу другого стовпця, збільшеному на норму вектору розмірності
, координати якого, починаючи з третьої, дорівнюють відповідним елементам другого стовпця, перша координата дорівнює нулю, а друга дорівнює другому елементу другого стовпця, збільшеному на норму вектору розмірності 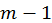 , координати якого суть елементи другого стовпця, починаючи з другого елемента.
, координати якого суть елементи другого стовпця, починаючи з другого елемента.
Далі обертають в нуль елементи другого рядка, починаючи з четвертого елемента, для чого вводять вектор 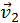 і за ним визначають перетворення
і за ним визначають перетворення 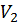 , і т.д.
, і т.д.
В результаті цього процесу отримаємо шукану двохдіагональну матрицю.
Перший етап алгоритму на цьому закінчується.
Пряме використання ортогональних перетворень не дозволяє отримати які-небудь нові нулі. Для матриці 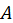 розмірності
розмірності 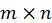 потрібно
потрібно 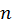 перетворень
перетворень 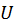 і
і 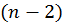 перетворень
перетворень 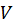 , щоб досягти цього місця, тобто отримати двохдіагональну матрицю. Число перетворень не залежить від кількості рядків, але від кількості рядків залежить робота, що витрачається на виконання кожного перетворення. Коли ранг заданої матриці менший за
, щоб досягти цього місця, тобто отримати двохдіагональну матрицю. Число перетворень не залежить від кількості рядків, але від кількості рядків залежить робота, що витрачається на виконання кожного перетворення. Коли ранг заданої матриці менший за 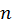 , кількість перетворень
, кількість перетворень 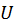 і
і 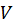 виявляється менше, оскільки після виконання деякого перетворення
виявляється менше, оскільки після виконання деякого перетворення 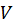 один або декілька подальших стовпців можуть мати на діагоналі і під діагоналлю(і навіть над діагоналлю) елементи порядку помилки округлення, тобто з розрахунковою точністю дорівнюють нулю. Ці нулі можуть зберегтися при подальших перетвореннях.
один або декілька подальших стовпців можуть мати на діагоналі і під діагоналлю(і навіть над діагоналлю) елементи порядку помилки округлення, тобто з розрахунковою точністю дорівнюють нулю. Ці нулі можуть зберегтися при подальших перетвореннях.
Другий етап алгоритму сингулярного розкладання матриці - обнулення елементів наддіагоналі є ітераційним процесом. Кожен його крок зменшує величину деякого елементу наддіагоналі. Кінець кінцем ці елементи стають порівнюваними з помилками округлень, і їх можна відкинути. Фактичне число кроків залежить від конкретної матриці і точності ЕОМ, але швидкість збіжності дуже висока так що зазвичай на виконання другого етапу вимагається менше часу, ніж на виконання першого. Це особливо вірно у випадку, коли 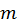 набагато більше, ніж
набагато більше, ніж 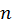 , оскільки на другому етапі зберігаються усі нулі, отримані нижче перших
, оскільки на другому етапі зберігаються усі нулі, отримані нижче перших 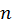 рядків.
рядків.
Отже, кожен ітераційний крок розпочинається з двохдіагональної матриці, яка перетвориться в іншу двохдіагональну матрицю з меншими за абсолютною величиною позадіагональними елементами. Для зменшення позадіагональних елементів використовуємо матриці обертання, при цьому можуть з’явитися ненульові елементи поза діагоналлю і наддіагоналлю. Для обнулення цих елементів також використовують матриці обертання. Значення 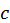 і
і 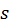 у матрицях обертання знаходять з системи відносно
у матрицях обертання знаходять з системи відносно 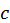 і
і 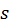 : перше рівняння цієї системи - умова нормування
: перше рівняння цієї системи - умова нормування 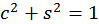 , а друге отримуємо з умови перетворення на нуль певного елементу перетворюваної матриці.
, а друге отримуємо з умови перетворення на нуль певного елементу перетворюваної матриці.
Таким чином, на другому етапі алгоритму будується послідовність
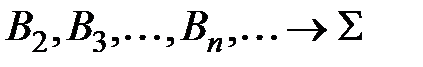
(нумерацію розпочато з двох для зручності), причому у матриці 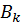 ,
, 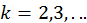 , елементи поза діагоналлю і наддіагоналлю дорівнюють нулю, елементи наддіагоналі зменшуються за абсолютною величиною зі збільшенням номера
, елементи поза діагоналлю і наддіагоналлю дорівнюють нулю, елементи наддіагоналі зменшуються за абсолютною величиною зі збільшенням номера 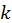 , а перехід
, а перехід 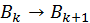 здійснюється за допомогою послідовності плоских обертань, тобто
здійснюється за допомогою послідовності плоских обертань, тобто
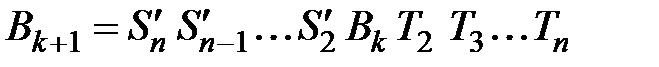 , (24)
, (24)
або
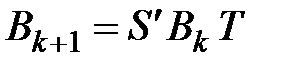 ,
,
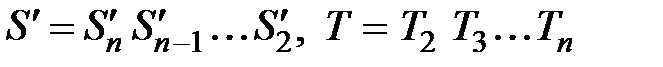 .
.
Введемо до розгляду трьохдіагональну матрицю 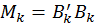 (не навпаки!). Матриці
(не навпаки!). Матриці  і
і 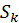 вибирають так, щоб послідовність матриць
вибирають так, щоб послідовність матриць 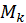 збігалася до діагональної матриці і щоб всі
збігалася до діагональної матриці і щоб всі 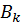 зберігали двохдіагональну форму.
зберігали двохдіагональну форму.
Матриця  має вигляд:
має вигляд:
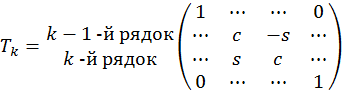 .
.
В цьому випадку досить для позначення матриці обертання одного індексу. Аналогічний вигляд має і матриця 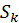 .
.
Перше обертання 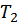 вибирається так, щоб послідовність матриць
вибирається так, щоб послідовність матриць 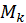 збігалася до діагональної матриці.
збігалася до діагональної матриці.
Неважко бачити, що
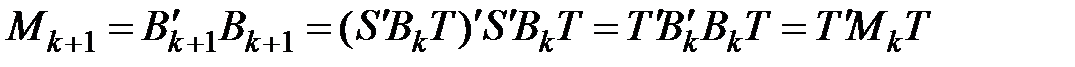 ,
,
тобто матриця 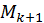 - трьохдіагональна і подібна до матриці
- трьохдіагональна і подібна до матриці 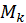 .
.
Значення 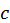 і
і 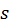 , що визначають матрицю
, що визначають матрицю 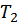 , слід вибирати так, щоб перетворення
, слід вибирати так, щоб перетворення 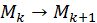 було
було 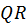 - перетворенням із зсувом, що дорівнює
- перетворенням із зсувом, що дорівнює 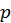 , а саме:
, а саме:
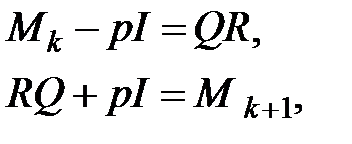 (25)
(25)
де 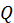 - ортогональна матриця, а
- ортогональна матриця, а 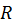 - верхня трикутна матриця. При цьому, як ми бачили раніше,
- верхня трикутна матриця. При цьому, як ми бачили раніше, 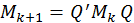 , тобто перетворення (24) еквівалентне
, тобто перетворення (24) еквівалентне 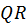 -перетворенню (25) із зсувом -
-перетворенню (25) із зсувом - 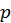 ;
; 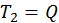 .
.
Параметр зсуву 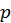 визначається власним значенням нижнього мінору (розмір
визначається власним значенням нижнього мінору (розмір 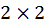 ) матриці
) матриці 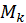 . При такому виборі параметра
. При такому виборі параметра 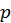 метод має глобальну і майже завжди кубічну збіжність.
метод має глобальну і майже завжди кубічну збіжність.
Проте перетворення 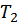 може зіпсувати двохдіагональну форму матриці
може зіпсувати двохдіагональну форму матриці 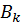 . Нехай, наприклад, у матриці
. Нехай, наприклад, у матриці 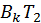 з'явився відмінний від нуля елемент в позиції (2;1). Подальші повороти
з'явився відмінний від нуля елемент в позиції (2;1). Подальші повороти 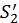 ,
, 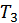 ,
, 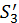 ,...,
,..., 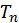 ,
, 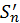 необхідно вибирати так, щоб матриця
необхідно вибирати так, щоб матриця 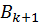 мала ту ж форму, що і
мала ту ж форму, що і 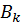 . Матриця
. Матриця 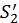 анулює елемент в позиції (2;1), але додає елемент (1;3);
анулює елемент в позиції (2;1), але додає елемент (1;3); 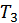 анулює елемент (1;3), але додає елемент (3;2) і т.д.; нарешті,
анулює елемент (1;3), але додає елемент (3;2) і т.д.; нарешті, 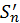 анулює елемент
анулює елемент 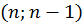 і нічого не додає (рис. 7).
і нічого не додає (рис. 7).
| * | ||||
| * | * | |||
| * | * | |||
| * | ||||
| * |
Рисунок 7 – Процес переслідування
Цей процес часто називають процесом переслідування.
Таким чином, ітераційний процес сконструйований так, щоб анулювати наддіагональні елементи, а теорема Уілкінсона стверджує, що ітерації завжди збігаються, і збіжність дуже швидка. Первинне приведення до двохдіагональної матриці не лише забезпечує можливість побудови ітераційного процесу, воно також прискорює його збіжність.
Отже, цей алгоритм - обчислювально стійкий і досить одноманітний, тому що використовує лише ортогональні перетворення (на першому етапі - перетворення відбиття, на другому етапі - перетворення обертання).
Приклад 31. За допомогою цього алгоритму побудуємо сингулярне розкладення матриці
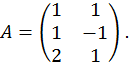
Перший етап.
Вектори
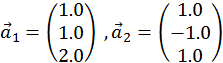
Евклідова норма
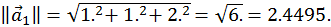
Вектор 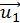 має вигляд
має вигляд
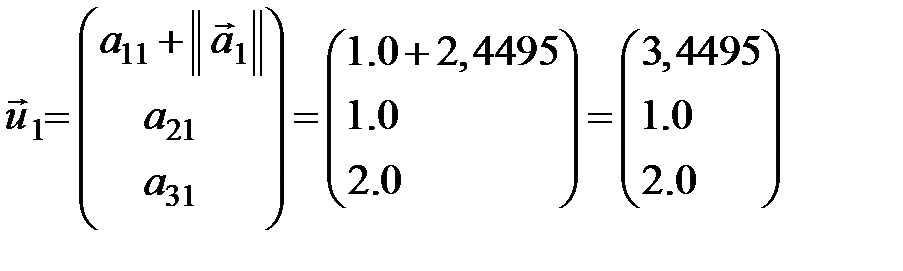 .
.
Позначимо
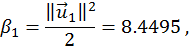
тоді 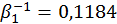 .
.
Знаходимо стовпці матриці 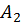 :
:
 ;
;
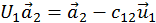 ;
; 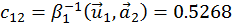 ;
;
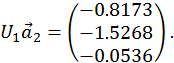
Матриця

Перетворення 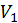 відсутнє, оскільки в матриці всього два стовпці.
відсутнє, оскільки в матриці всього два стовпці.
Обнуляємо елементи в другому стовпці під діагоналлю. Розглядаємо вектор
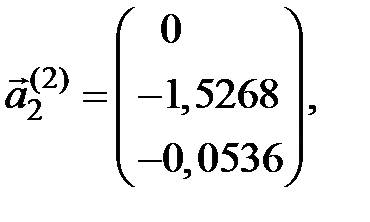
його норма Евкліда дорівнює 1,5277.
Вектори
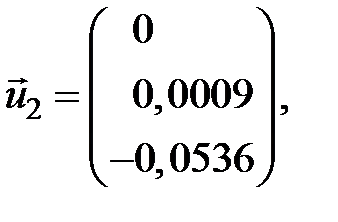
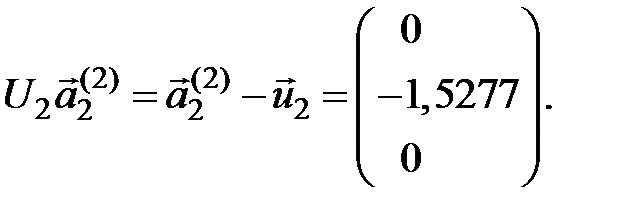
Матриця
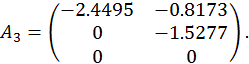
Перший етап на цьому закінчується.
Другий етап.
Розглядаємо двохдіагональну матрицю
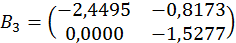
(нульовий рядок матриці 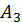 залишається таким в усіх подальших перетвореннях і тому може бути випущений).
залишається таким в усіх подальших перетвореннях і тому може бути випущений).
Будуємо перетворення 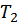 . Для цього знаходимо матрицю
. Для цього знаходимо матрицю
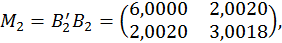
власні значення якої дорівнюють 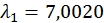 та
та 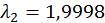 .
.
Візьмемо 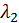 в якості параметра зсуву
в якості параметра зсуву 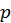 , тобто
, тобто 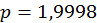 ; тоді перший стовпець матриці
; тоді перший стовпець матриці 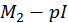 буде
буде 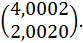
З формули 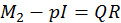 отримуємо рівність
отримуємо рівність 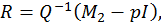
з якої знаходимо елементи 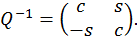
Таким чином, щоб у матриці 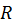 елемент
елемент 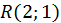 дорівнював нулю, для
дорівнював нулю, для 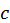 і
і 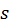 маємо:
маємо:
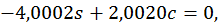
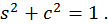
Звідси 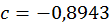 , а
, а 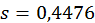 . Вибір знаку при визначенні кореня байдужий, але для перетворення
. Вибір знаку при визначенні кореня байдужий, але для перетворення 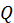 знак
знак 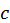 краще узяти співпадаючим зі знаком елементу матриці
краще узяти співпадаючим зі знаком елементу матриці 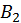 в позиції
в позиції 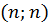 .
.
Далі:
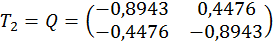
та
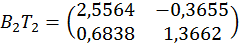 .
.
Тепер підбираємо перетворення 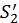 , що анулює елемент в позиції (2;1).
, що анулює елемент в позиції (2;1).
Нехай
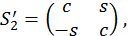
тоді
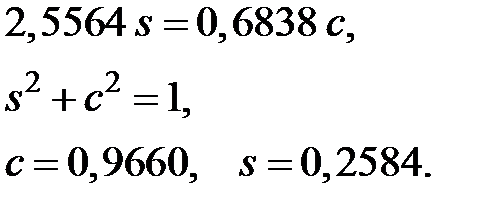
Нарешті, матриця
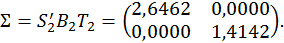
Зауважимо, що елементи матриці S мають чотири правильні цифри. Для отримання більшої точності обчислення слід вести з більшою кількістю знаків.
Відповіді
1 . a) 2; б) 4 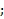 в) 4; г) 4; д)
в) 4; г) 4; д) 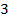 ; е) 6; ж) 4; з) 4.
; е) 6; ж) 4; з) 4.
2. a) 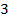 ; б)
; б) 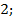 в)
в) 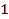 ; г)
; г) 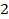 ; д)
; д) 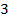 .
.
3. 0.
4. 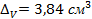 ;
; 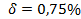 .
.
5. 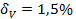 .
.
6. 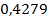 ;
; 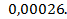
7. 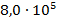 ;
; 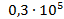 .
.
8. 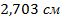 ;
; 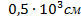 .
.
9. 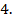
10. 6.
11. 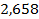 ;
; 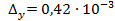 ;
; 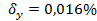 .
.
12. 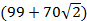 ;
; 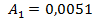 ;
; 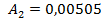 ;
; 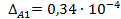 ;
;
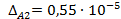 ;
; 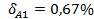 ;
; 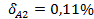 .
.
14. 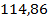 .
.
15. 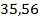 .
.
16. 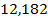 ;
; 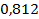 .
.
17. 0,185.
18. 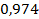 .
.
19. 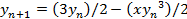 ;
; 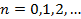 .
.
20. 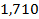 .
.
21. 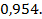
22.
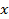
| 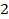
| 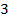
| 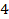
| 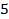
| 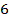
| 
| 
| 
| 
|
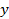
| 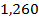
| 1,442 | 1,587 | 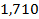
| 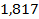
| 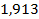
| 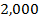
| 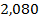
| 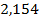
|
23. 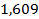 . 24.
. 24. 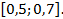
25. 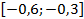 . 26.
. 26. 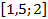 . 27.
. 27. 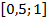 .
.
28. 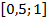 . 29.
. 29. 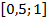 . 30.
. 30. 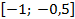 ;
; 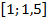 .
.
31. 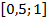 . 32.
. 32. 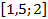 . 33.
. 33. 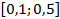 .
.
34. 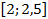 . 35.
. 35. 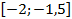 ;
; 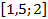 .
.
36. 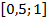 ;
; 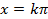 ;
; 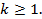
37. 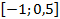 ;
; 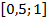 . 38.
. 38. 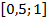 .
.
39. 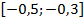 ;
;  . 40.
. 40. 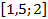 .
.
41. 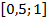 ;
; 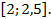
42. 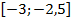 ;
;  ;
; 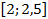 .
.
43. 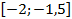 ,
, 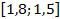 ,
, 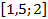 .
.
44. 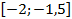 ;
; 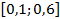 ;
; 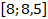 .
.
45 . 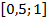 ,
, 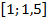 .
.
24 ’. 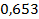 . 25 ’. . 25 ’. 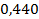 . 26 ’. . 26 ’.  . 27 ’. . 27 ’. 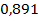 . 28 ’. . 28 ’. 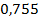 . 29 ’. . 29 ’. 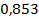 . 30 ’. . 30 ’. 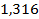 .
31 ’. .
31 ’. 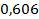 . 32 ’. . 32 ’. 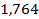 . 33 ’. . 33 ’. 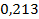 . 34 ’. . 34 ’. 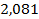 . 35 ’. . 35 ’. 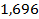 ; ; 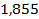 .
36 ’. .
36 ’. 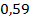 ; ; 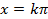 ; ; 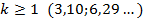 .
37 ’. .
37 ’. 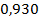 . 38 ’. . 38 ’. 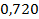 . 39 ’. . 39 ’. 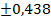 . 40 ’. . 40 ’. 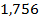 . 45 ’. . 45 ’. 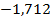 ; ; 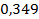 ; ; 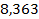 . .
|
46. 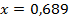 ;
; 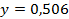 . 47.
. 47. 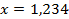 ;
; 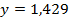 .
.
48. 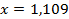 ;
; 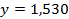 . 49.
. 49. 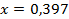 ;
; 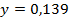 .
.
50. 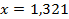 ;
; 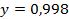 . 51.
. 51. 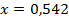 ;
; 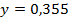 .
.
52. 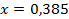 ;
; 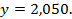 53.
53. 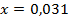 ;
; 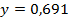 .
.
54. 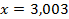 ;
; 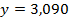 . 55.
. 55. 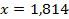 ;
; 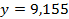 .
.
56. 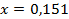 ;
; 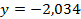 . 57.
. 57. 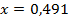 ;
; 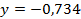 .
.
58. 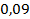 ;
; 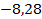 . 59.
. 59. 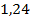 ;
; 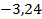 .
.
60. 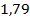 ;
; 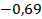 . 61.
. 61. 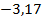 ;
; 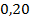 .
.
62. 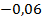 ;
; 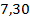 . 63.
. 63. 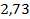 ;
; 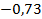 .
.
64. 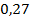 ;
; 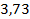 . 65.
. 65. 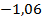 ;
; 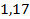 .
.
66. 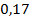 ;
; 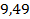 . 67.
. 67. 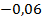 ;
; 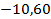 .
.
68. 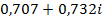 . 69.
. 69. 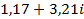 .
.
70. 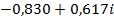 Вказівка. Перейти до розгляду рівняння
Вказівка. Перейти до розгляду рівняння 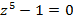 .
.
71. 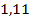 ;
; 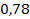 ;
; 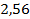 . 72.
. 72. 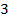 ;
; 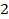 ;
; 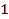 .
.
73. 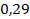 ;
; 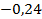 ;
; 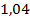 . 74.
. 74. 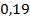 ;
; 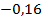 ;
; 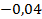 .
.
75. 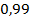 ;
; 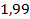 ;
; 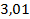 . 76.
. 76. 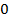 ;
; 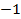 ;
; 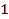 .
.
77. 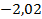 ;
; 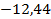 ;
; 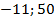 . 78.
. 78. 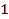 ;
; 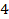 ;
; 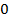 ;
; 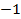 .
.
79. 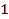 ;
; 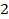 ;
; 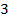 ;
; 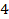 . 80.
. 80. 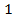 ;
; 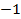 ;
; 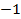 ;
; 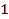 .
.
81. 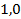 ;
; 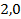 ;
; 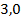 ;
; 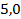 .
.
82. 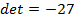
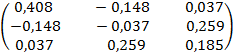
83. 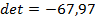
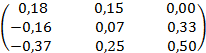
84. 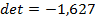
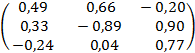
Список рекомендованої літератури
1. Бахвалов Н. С. Численные методы. – М.: Наука, 1987. – 600 с.
2. Березин И. С., Жидков Н. П. Методы вычислений. Т. 1. –М.: Наука, 1966. – 632 с.
3. Вержбицкий В. М. Основы численных методов. – М.: Высшая школа, 2002. – 840 с.
4. Вержбицкий В. М. Численные методы. – М.: Высшая школа, 2001. – 382 с.
5. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
6. Калиткин Н. Н. Численные методы. – М.: Наука, 1978. – 512 с.
7. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368 с.
8. Ляшко И. И., Макаров В. Л., Скоробогатько А. А. Методы вычислений. – Киев: Высшая школа, 1977. – 408 с.
9. Марчук Г. И. Методы вычислительной математики. – М.: Наука, 1989. – 608 с.
10. Положий Г. Н. и др. Математический практикум. Под ред. Положего. М.: ГИФМЛ,1960. – 512 с.
11. Самарский А. А. Введение в численные методы. – М.: Изд-во “Лань”, 2005. – 288 с.
12. Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры. – М.: Физматгиз. – 1960. – 734 с.
Дата: 2019-03-05, просмотров: 319.