Нехай рівняння (6) алгебраїчне, тобто 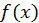 – многочлен. Розглянемо метод Берстоу для виділення квадратичного множника
– многочлен. Розглянемо метод Берстоу для виділення квадратичного множника 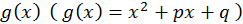 алгебраїчного многочлена
алгебраїчного многочлена 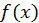 , причому корені многочлена
, причому корені многочлена 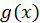 обов’язково мають бути різні. Розділивши
обов’язково мають бути різні. Розділивши 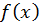 на
на 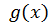 , можемо записати
, можемо записати
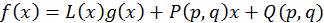
Очевидно, якщо 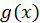 – дільник
– дільник 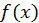 , то
, то

і, таким чином, задача зводиться до розв’язання системи (10). Ця система розв’язується методом Ньютона, а використовувані в цьому методі значення функцій 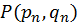 ,
, 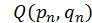 , і їх похідних
, і їх похідних 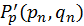 ,
, 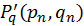 ,
, 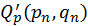 ,
, 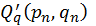 знаходяться таким чином. Поділимо
знаходяться таким чином. Поділимо 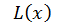 на
на 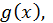 тоді
тоді
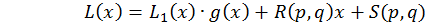 ,
,
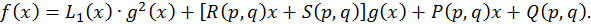
Продиференціюємо останню тотожність по 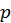 і по
і по 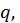 отримаємо рівність:
отримаємо рівність:
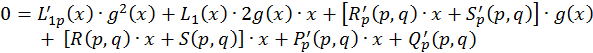 ,
,
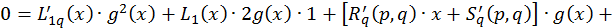
 .
. 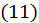
Нехай 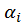 (
( 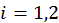 ) - корені дільника
) - корені дільника 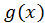 , тобто
, тобто 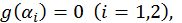 причому
причому 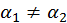 . Підставляючи
. Підставляючи 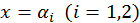 в рівності (11) і враховуючи, що
в рівності (11) і враховуючи, що 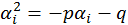 , матимемо
, матимемо
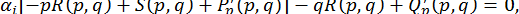
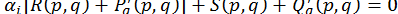 .
.
Звідси, оскільки 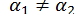 , отримаємо
, отримаємо
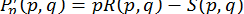 ,
, 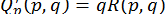 ,
,
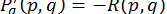 ,
, 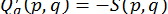 .
. 
Таким чином, ми виразили похідні функцій 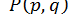 і
і 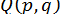 по
по 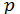 і
і 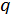 через
через 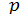 ,
, 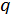 ,
, 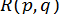 ,
, 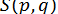 . Тому, знаючи
. Тому, знаючи 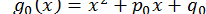 і виконавши двічі ділення на
і виконавши двічі ділення на 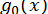 спочатку многочлена
спочатку многочлена 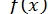 , а потім частки
, а потім частки 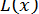 , ми знайдемо
, ми знайдемо  ,
, 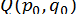 ,
, 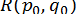 ,
, 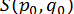 . Після цього за формулами (12) обчислюємо
. Після цього за формулами (12) обчислюємо 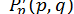 ,
, 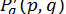 ,
, 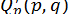 ,
, 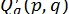 , і, застосовуючи метод Ньютона для системи (10), знаходимо
, і, застосовуючи метод Ньютона для системи (10), знаходимо 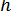 та
та 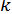 , потім
, потім 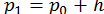 ,
, 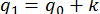 та
та 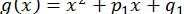 . Далі, увесь процес повторюємо спочатку.
. Далі, увесь процес повторюємо спочатку.
При вдалому виборі початкового наближення метод, очевидно, збігається.
Для побудови початкового наближення 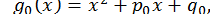 що відповідає дійсним кореням, можна знайти графічно або за допомогою теореми про нуль неперервної на відрізку функції початкові наближення к двом різним дійсним кореням
що відповідає дійсним кореням, можна знайти графічно або за допомогою теореми про нуль неперервної на відрізку функції початкові наближення к двом різним дійсним кореням 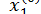 і
і 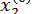 функції
функції 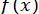 , тоді
, тоді
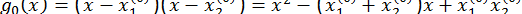 , тобто
, тобто 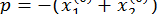 , а
, а 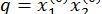 . Іноді початкові наближення вдається знайти за допомогою теореми Вієта.
. Іноді початкові наближення вдається знайти за допомогою теореми Вієта.
ПРИКЛАД 22. Знайти з точністю до 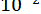 методом Берстоу квадратичний множник многочлена
методом Берстоу квадратичний множник многочлена 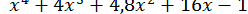 і обчислити його корені.
і обчислити його корені.
Груба прикидка показує, що рівняння має два дійсні корені ( 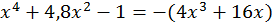 ; рис. 5), щоб відокремити їх, визначимо знак функції
; рис. 5), щоб відокремити їх, визначимо знак функції 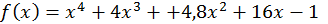 при деяких значеннях
при деяких значеннях 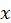 :
:
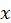
| 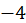
| 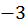
| 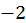
| 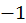
| 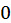
| 
|

| 
| 
| 
| 
| 
| 
|
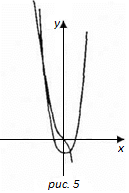
Рисунок 5 – Графіки функцій  .
.
Візьмемо 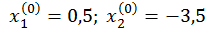 . Тоді
. Тоді 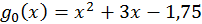 ; тобто
; тобто 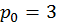 ,
, 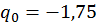 . Ділимо, далі,
. Ділимо, далі, 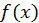 і
і  на
на 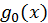
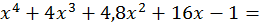
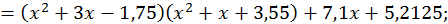
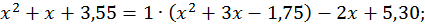
тобто
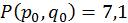 ;
; 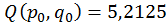 ;
; 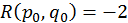 ;
; 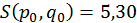 .
.
Отже, 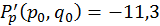 ;
; 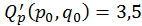 ;
;
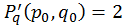 ;
; 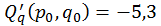
і система для поправок ℎ і 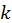 має вигляд
має вигляд
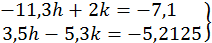
Звідси 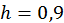 ;
; 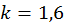 . Далі,
. Далі, 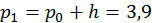 ;
;
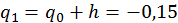 ;
; 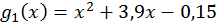 .
.
На другому кроці отримуємо
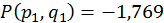 ;
; 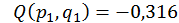 ;
; 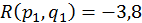 ;
; 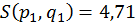 ;
;
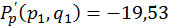 ;
; 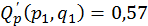 ;
;
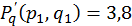 ;
; 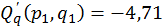 ;
;
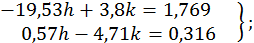
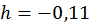 ;
; 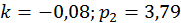 ;
; 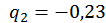 ;
;
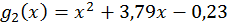 .
.
На третьому кроці
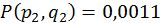 ;
; 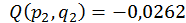 ;
; 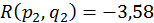 ;
; 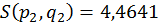 ;
;
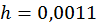 ;
; 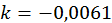 ;
; 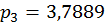 ;
; 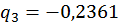 .
.
Оскільки з точністю до 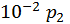 і
і 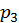 , а також
, а також 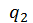 і
і 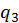 співпадають, то
співпадають, то 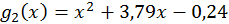 . Проте, при обчисленні коренів візьмемо
. Проте, при обчисленні коренів візьмемо 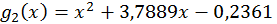 (із запасними знаками):
(із запасними знаками):
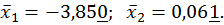
А оскільки
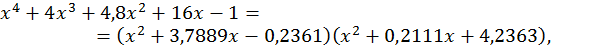
то інші два корені заданого рівняння 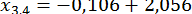 .
.
При розв’язанні алгебраїчних рівнянь слід враховувати, що значення многочлена швидко ростуть зі збільшенням 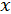 і тому можливе переповнення. Для зменшення похибки округлення при розв’язанні методом Берстоу алгебраїчного рівняння високого степеня починати слід з найменших по модулю коренів, а потім знайдені корені видаляють і процедуру повторюють.
і тому можливе переповнення. Для зменшення похибки округлення при розв’язанні методом Берстоу алгебраїчного рівняння високого степеня починати слід з найменших по модулю коренів, а потім знайдені корені видаляють і процедуру повторюють.
Задачі
Методом Берстоу з точністю до 0,01 знайти дійсні корені алгебраїчних рівнянь:
58. 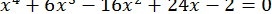 .
.
59. 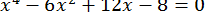 .
.
60. 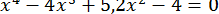 .
.
61. 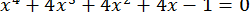 .
.
62. 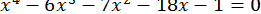 .
.
63. 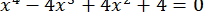 .
.
64. 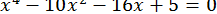 .
.
65. 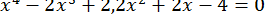 .
.
66. 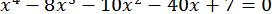 .
.
67. 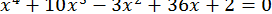 .
.
Дата: 2019-03-05, просмотров: 323.