Нехай треба знайти з точністю 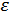 корінь рівняння (6), що міститься в інтервалі
корінь рівняння (6), що міститься в інтервалі 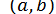 .
.
Найбільш простим методом уточнення коренів є метод ділення навпіл. При цьому відрізок 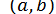 , що містить корінь, ділиться навпіл, і надалі розглядається та його половина, яка містить корінь, тобто функція
, що містить корінь, ділиться навпіл, і надалі розглядається та його половина, яка містить корінь, тобто функція 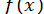 на її кінцях має різні знаки. Для знаходження наближеного до кореня значення
на її кінцях має різні знаки. Для знаходження наближеного до кореня значення 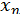 з точністю
з точністю 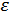 процес ділення навпіл продовжуємо до тих пір, поки не виконуватиметься нерівність
процес ділення навпіл продовжуємо до тих пір, поки не виконуватиметься нерівність 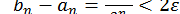 , де
, де 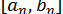 - відрізок після
- відрізок після 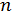 -го ділення, що містить корінь, тобто
-го ділення, що містить корінь, тобто 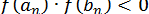 . Після цього вважаємо
. Після цього вважаємо 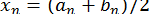 ; тоді, очевидно,
; тоді, очевидно, 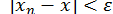 . Якщо функція
. Якщо функція 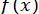 диференційована, вигідніше користуватися оцінкою
диференційована, вигідніше користуватися оцінкою
 (8)
(8)
де 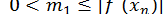 для
для 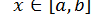 . Якщо на
. Якщо на 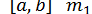 виявиться рівним нулю, то відрізок
виявиться рівним нулю, то відрізок 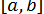 слід звузити. Як тільки
слід звузити. Як тільки 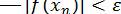 , процес ділення навпіл закінчується.
, процес ділення навпіл закінчується.
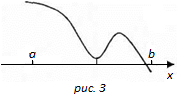
Рисунок 3
Відмітимо, що процес ділення навпіл не слід закінчувати на тій основі, що 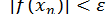 . Це видно на рис. 3. Метод ділення навпіл надзвичайно простий, але збігається, як правило, повільно. Цей метод легко реалізується на ЕОМ, при цьому
. Це видно на рис. 3. Метод ділення навпіл надзвичайно простий, але збігається, як правило, повільно. Цей метод легко реалізується на ЕОМ, при цьому 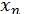 слід визначати по формулі
слід визначати по формулі
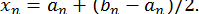
Щоб зрозуміти це, візьміть 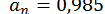 ;
; 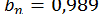 та обчисліть
та обчисліть 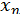 на машині з тризначною десятковою плаваючою арифметикою за обома формулами. Крім того, перевіряти на ЕОМ, чи містить відрізок
на машині з тризначною десятковою плаваючою арифметикою за обома формулами. Крім того, перевіряти на ЕОМ, чи містить відрізок 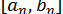 корінь, за допомогою нерівності
корінь, за допомогою нерівності 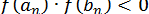 не можна, тому що цей добуток може виявитися машинним нулем.
не можна, тому що цей добуток може виявитися машинним нулем.
ПРИКЛАД 16. Знайти з точністю 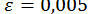 позитивний корінь рівняння
позитивний корінь рівняння
 .
.
Шуканий корінь належить відрізку 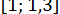 , причому
, причому 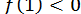 ,
,  ;
; 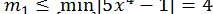 . Після першого ділення отримуємо
. Після першого ділення отримуємо
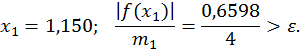
Далі,
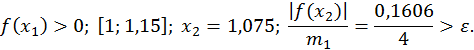
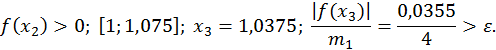
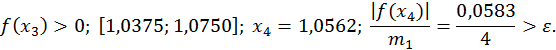
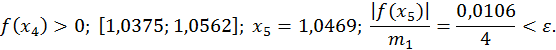
Значить, 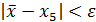 та
та 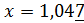 з точністю
з точністю 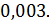
Метод простої ітерації
Метод простої ітерації для уточнення коренів рівняння (6) полягає в наступному. Рівняння (6) зводиться до вигляду

причому має бути виконана умова збіжності
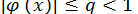 для
для 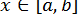 .
.
На відрізку 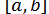 вибираємо початкове наближення
вибираємо початкове наближення 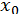 (
( 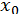 краще брати з середньої третини відрізку
краще брати з середньої третини відрізку 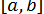 , інакше похибка округлення може вивести нас за межі того відрізку, де виконується умова збіжності) і знаходимо подальші наближення до кореня за формулою
, інакше похибка округлення може вивести нас за межі того відрізку, де виконується умова збіжності) і знаходимо подальші наближення до кореня за формулою

Ітерації 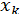 обчислюємо до виконання умови
обчислюємо до виконання умови
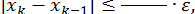
тоді з оцінки точності цього методу
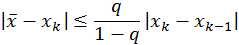
випливає, що 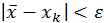 .
.
Помітимо, що у випадку, коли 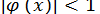 і
і 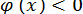 , послідовні наближення збігаються до кореня, коливаючись відносно кореня (
, послідовні наближення збігаються до кореня, коливаючись відносно кореня ( 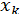 праворуч,
праворуч, 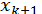 ліворуч,
ліворуч, 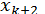 праворуч і так далі). В цьому випадку
праворуч і так далі). В цьому випадку
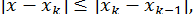
і, отже, знаки наближення 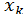 , що встановилися, обов’язково належать до точного значення кореня
, що встановилися, обов’язково належать до точного значення кореня 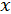 .
.
ПРИКЛАД 17. Методом простої ітерації знайти з точністю 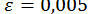 позитивний корінь рівняння
позитивний корінь рівняння

Зведемо це рівняння до вигляду  :
:
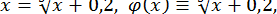 та
та
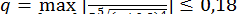 .
.
Візьмем 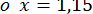 , тоді
, тоді
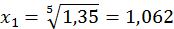 ;
; 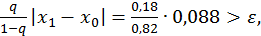
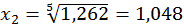 ;
; 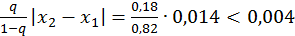 .
.
Значить, 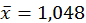 з точністю
з точністю 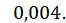
ПРИКЛАД 18. Методом простої ітерації знайти з точністю до 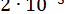 позитивний корінь рівняння
позитивний корінь рівняння
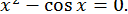
Раніше було знайдено, що 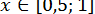 . Далі,
. Далі, 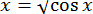 , тобто
, тобто
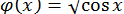 ;
; 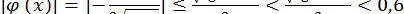 .
.
Для всіх 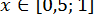
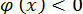 . Значить, наближення
. Значить, наближення 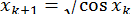 збігаються до кореня коливаючись
збігаються до кореня коливаючись
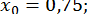
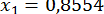 ;
; 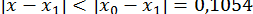 ;
;
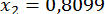 ;
; 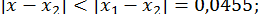
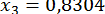 ;
; 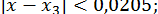
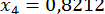 ;
; 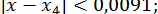
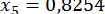 ;
; 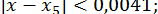
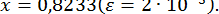
На швидкість збіжності методу ітерацій впливає вибір початкового приближения 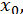 а також величина
а також величина 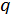 .
.
Зведення рівняння (6) до вигляду (9) можна здійснити різними способами. Так, в прикладі 17, безпосередньо виражаючи 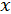 з рівняння, отримуємо
з рівняння, отримуємо 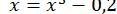 ;
;
або 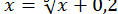 ;
;
або 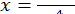 та ін.
та ін.
Очевидно, при відшукуванні кореня, що належить відрізку 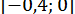 , можна ітерувати перше з цих рівнянь, але воно не придатне для кореня з відрізку
, можна ітерувати перше з цих рівнянь, але воно не придатне для кореня з відрізку 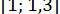 .
.
У разі, якщо це рівняння має вигляд 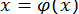 , але в околі шуканого кореня
, але в околі шуканого кореня 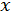 має місце нерівність
має місце нерівність
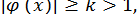
то замінюємо це рівняння еквівалентним
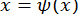 ,
,
де 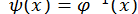 , для цього рівняння процес ітерації збігатиметься, оскільки
, для цього рівняння процес ітерації збігатиметься, оскільки

Так, при знаходженні коренів рівняння 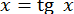 слід ітерувати рівняння
слід ітерувати рівняння
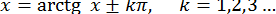
Вельми корисним на практиці виявляється наступний спосіб зведення рівняння (6) до вигляду (9). Нехай корінь 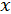 рівняння (6) належить відрізку
рівняння (6) належить відрізку 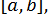 і для
і для 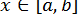 виконується нерівність
виконується нерівність
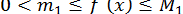
(важливо, що похідна зберігає знак на 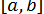 ).
).
Покладемо тоді
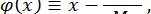
умова збіжності виконується, оскільки
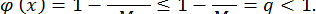
Наприклад, для рівняння  маємо
маємо 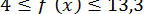 для будь-якого
для будь-якого 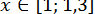 , і отже, для відшукування кореня з цього відрізку можна ітерувати рівняння
, і отже, для відшукування кореня з цього відрізку можна ітерувати рівняння

при цьому 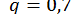 . Виходячи з
. Виходячи з 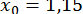 (приклад 17) для досягнення точності
(приклад 17) для досягнення точності 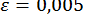 потрібно виконати 7 ітерацій (у прикладі 17 всього дві ітерації).
потрібно виконати 7 ітерацій (у прикладі 17 всього дві ітерації).
Це показує, як важливо при зведенні рівняння (6) до вигляду (9) добитися, щоб 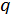 було якнайменшим.
було якнайменшим.
Метод хорд і метод дотичних
Метод хорд і метод дотичних є різновидами методу ітерації при спеціальному виборі функції 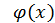 . В методі хорд
. В методі хорд  , де
, де 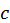 – так звана нерухома точка, в якості
– так звана нерухома точка, в якості 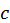 береться той з кінців відрізку
береться той з кінців відрізку 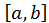 , де
, де 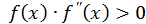 , інший кінець цього відрізку береться за початкове наближення
, інший кінець цього відрізку береться за початкове наближення 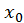 , ітерації будуються по формулі
, ітерації будуються по формулі
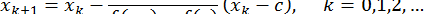
(до спільного знаменника не зводити! Чому?).
У методі дотичних 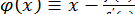 , за початкове наближення
, за початкове наближення 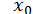 вибирається один з кінців відрізку
вибирається один з кінців відрізку 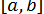 , саме той, де
, саме той, де  . Робоча формула методу має вигляд
. Робоча формула методу має вигляд

Для закінчення процесу ітерацій в методі дотичних можна використати наступну оцінку точності
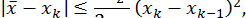
де
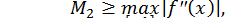 а
а 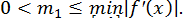
Крім того, оцінювати похибку наближень 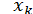 в усіх методах можна за загальною оцінкою (8).
в усіх методах можна за загальною оцінкою (8).
В методах хорд і дотичних корінь бажано відокремити так, щоб 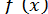 та
та 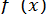 зберігали знак на [a, b] (інакше метод може виявитися непридатним).
зберігали знак на [a, b] (інакше метод може виявитися непридатним).
З оцінок точності методів видно, що метод дотичних (Ньютона) збігається швидше за інші. Це - метод другого порядку точності.
ПРИКЛАД 19. Методом хорд і методом дотичних знайти з точністю до 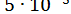 позитивний корінь рівняння
позитивний корінь рівняння

В методі хорд 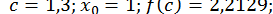
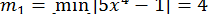 .
.



Отже, 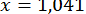 .
.
В методі дотичних 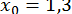 ;
; 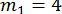 ;
;  .
.
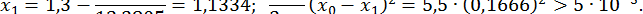
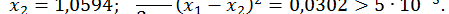
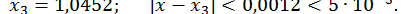
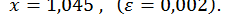
Помітимо, що в методі дотичних початкове наближення 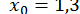 виявилося найгрубішим, цим пояснюється велика кількість (порівняно з іншими методами) ітерацій.
виявилося найгрубішим, цим пояснюється велика кількість (порівняно з іншими методами) ітерацій.
Комбінований метод
Оскільки наближення до кореня, що отримуються методом хорд та дотичних, лежать по різні сторони від кореня 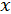 , то дуже вигідно поєднувати ці методи. Отримуємо так званий комбінований метод, він застосовується на кожному кроці до нового відрізку, або до
, то дуже вигідно поєднувати ці методи. Отримуємо так званий комбінований метод, він застосовується на кожному кроці до нового відрізку, або до 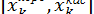 , якщо правий кінець нерухомий, або до
, якщо правий кінець нерухомий, або до 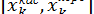 , якщо залишається нерухомим лівий кінець. Очевидно, що середина відрізку є наближенням до кореня з точністю
, якщо залишається нерухомим лівий кінець. Очевидно, що середина відрізку є наближенням до кореня з точністю

Так, в даному прикладі після першого кроку отримуємо
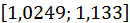 ; далі,
; далі, 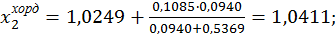

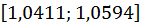 ; далі,
; далі, 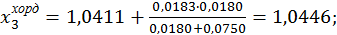

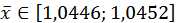 .
.
Довжина останнього відрізку дорівнює 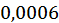 , отже, значення
, отже, значення 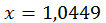 є наближенням до кореня з точністю
є наближенням до кореня з точністю 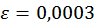 .
.
Дата: 2019-03-05, просмотров: 510.