У тому випадку, коли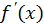 
мало змінюється на даному відрізку, корисним може виявитися модифікований метод Ньютона (дотичних) :
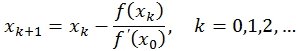
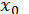вибирається так само, як і в звичайному методі дотичних, точність цього методу можна оцінити за формулою 
.
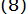Для даного рівняння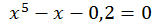 
отримаємо:
;
; 
; 
; 
;
; 
; 
; 
;
; 
; 
; 
;
.
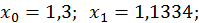
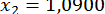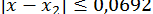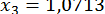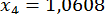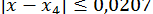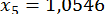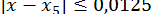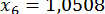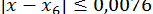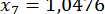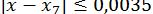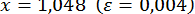Зауважимо, що використовують методи з похідними лише тоді, коли обчислення похідних не є занадто трудомістким.
У тому випадку, коли похідні складні і застосування оцінок скрутне, уточнення кореня роблять до збігу двох послідовних наближень із заданою точністю.
Іноді, наприклад, поблизу кратного кореня, може відбуватися втрата значущих цифр, що призводить до "розхитування" підрахунку. Це обмежує точність, з якою можна знайти корінь. Від "розхитування" страхуються таким чином (прийом Гарвика) : вибирають не дуже мале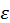 
і ведуть ітерації до виконання умови 
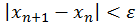, потім продовжують розрахунки до тих пір, поки 
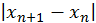убувають (зростання 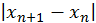зазвичай означає початок "розхитування").
Зауважимо дуже важливу властивість ітераційних методів: помилки округлення в ітераційних методах не накопичуються від ітерації до ітерації.
Метод січних
Ефективним методом розв’язання рівняння (6) є також метод січних:
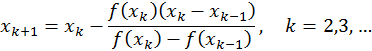
(до спільного знаменника не зводити!),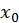 
та 
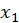вибираються, взагалі кажучи, довільно з [a, b] . Фактично цей метод виходить з методу дотичних заміною 
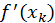відношенням 
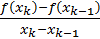. Оскільки
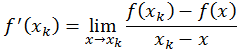
то за умови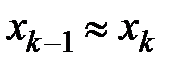 
матимемо 
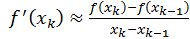. Достатні умови збіжності методу такі ж, як методу дотичних.
ПРИКЛАД 20. Методом січних знайти з точністю до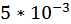 
позитивний корінь рівняння
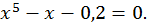
Візьме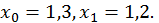мо 
Маємо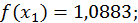 
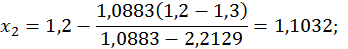
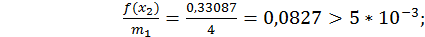
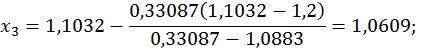
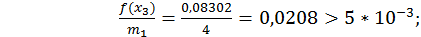
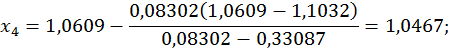
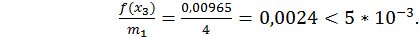
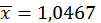з точністю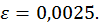 
Задачі
Уточнити корені рівнянь в задачах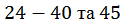 
з точністю до 
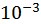усіма розглянутими методами (номери у відповідях - 
).
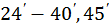3.8 Метод Ньютона для розв’язання нелінійних систем рівнянь
Оскільки теорія алгебраїчних многочленів добре розвинена, то для алгебраїчних рівнянь розроблено ряд спеціальних методів розв’язання, найбільш ефективним з них є метод Берстоу. Цей метод грунтується на методі Ньютона для розв’язання нелінійних систем рівнянь, тому спочатку розглянемо метод Ньютона. Нехай дана система двох нелінійних рівнянь
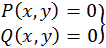
і відоме деяке наближення до її розв’язку, тобто відомі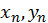 
, зокрема, це може бути початкове наближення 
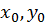, яке для випадку двох рівнянь можна знайти з графіку (розв’язок системи 
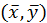- координати точки перетину кривих 
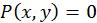та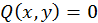 
).
Вважаючи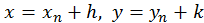 
, матимемо
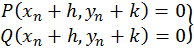
Застосовуємо формулу Тейлора, обмежуючись лінійними членами відносно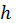 
і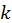 
, отримуємо
( 
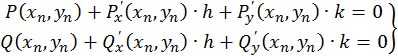
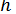і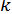 
, очевидно, можуть бути знайдені лише приблизно).
З цієї системи знаходимо 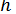і 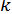, а потім
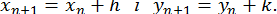
Якщо розв’язок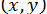 
простий і функці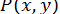ї 
і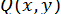 
мають неперервні похідні другого порядку в околиці розв’язку, то метод Ньютона збігається для будь-якої точки 
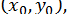досить близької до 
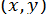. Оскільки гарних оцінок точності методу немає, то зазвичай ітерації продовжують до збігу двох послідовних наближень із заданою точністю.
Основна трудність при розв’язанні нелінійних систем рівнянь полягає в знаходженні початкового наближення; воно повинне належати деякій, взагалі кажучи, малій околиці шуканого розв’язку.
Як вже відзначалося, вибрати початкове наближення можна за допомогою графіку, іноді це вдається зробити підбором. Бажано враховувати і фізичні міркування.
ПРИКЛАД 21. Знайти методом Ньютона з точністю до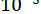 
розв’язок нелінійної системи
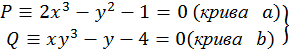
Початкове наближення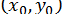 
знаходимо графічно: 
; 
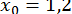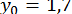(рис. 4.)
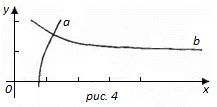
Рисунок 4 - Знаходження початкового наближення
; 
;
; 
.
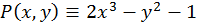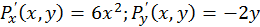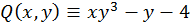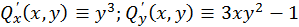Обчислюючи функції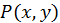 
, 
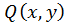та їх похідні в точці 
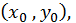приходимо до системи
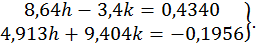
Перше рівняння зводимо до вигляду
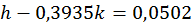
і виключаємо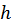 
з другого рівняння
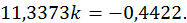
Значить,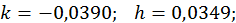 
Виходячи з цих значень, так само знаходимо
отже, розв’язок системи з точністю до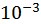
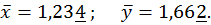
Для системи
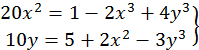
початкове наближення легко знайти підбором: з розгляду "близьких" рівнянь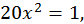 
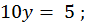
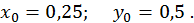
На першому кроці лінеаризована система має вигляд
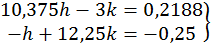
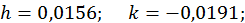
Далі,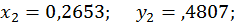 
Підбором неважко знайти початкове наближення такої системи
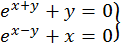
Очевидно,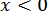 
, 
, 
, 
, 
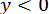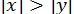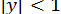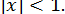
Декілька проб дають нам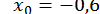 
; 
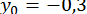. Уточнюючи ці значення за методом Ньютона, отримаємо 
; 
( 
).
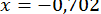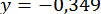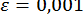Задачі
Знайти методом Ньютона з точністю до 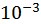один розв’язок (у І або ІІ квадранті) наступних нелінійних систем
46. 
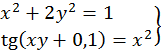
47. 
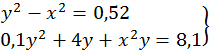
48. 
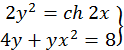
49. 
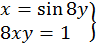
50. 
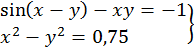
51. 
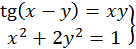
52. 
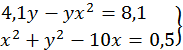
53. 
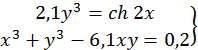
54. 
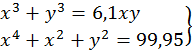
55. 
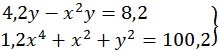
56. 
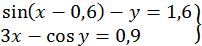
57. 
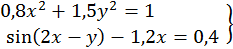
Дата: 2019-03-05, просмотров: 202.
