Побудуємо ітераційний процес для обчислення значень функції 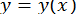 , яка задана неявно, тобто за допомогою рівняння
, яка задана неявно, тобто за допомогою рівняння
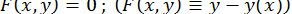 .
.
Нехай 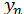 - наближене значення функції
- наближене значення функції 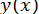 у деякій точці
у деякій точці 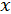 . Тоді
. Тоді
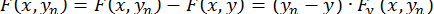
де 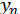 – деяке проміжне значення між
– деяке проміжне значення між 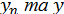 . І отже,
. І отже,

Замінюючи в останній формулі невідоме значення 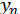 на відоме
на відоме 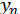 , отримуємо формулу для уточненого значення функції
, отримуємо формулу для уточненого значення функції 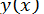 в точці
в точці 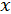 :
:
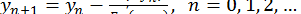 (5)
(5)
Якщо похідні 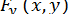 і
і 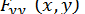 існують і зберігають постійні знаки в інтервалі, що містить шукане значення, то ітераційний процес при досить хорошому початковому наближенні збігається до
існують і зберігають постійні знаки в інтервалі, що містить шукане значення, то ітераційний процес при досить хорошому початковому наближенні збігається до 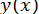 . Початкове значення
. Початкове значення 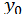 вибирають, по можливості, близьким до істинного значення
вибирають, по можливості, близьким до істинного значення 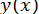 . Процес ітерації продовжують до тих пір, поки в межах заданої точності два послідовні наближення
. Процес ітерації продовжують до тих пір, поки в межах заданої точності два послідовні наближення 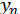 та
та 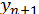 не співпадуть між собою. Після цього вважають
не співпадуть між собою. Після цього вважають 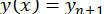 , при цьому, звичайно, не гарантується що
, при цьому, звичайно, не гарантується що 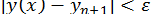 , для цього потрібне додаткове дослідження.
, для цього потрібне додаткове дослідження.
ПРИКЛАД 12. Обчислення квадратного кореня.
Нехай 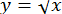 ,
, 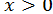 . Тоді
. Тоді 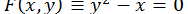 і формула
і формула 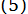 має вигляд
має вигляд 
Це відома формула Герона. Ітераційний процес за формулою Герона легко програмується на ЕОМ, причому процес збігається при будь-якому виборі 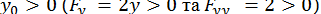 .
.
Обчислимо за цією формулою 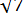 з точністю до
з точністю до 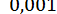 :
:
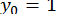 ;
;
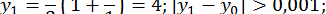
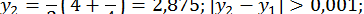
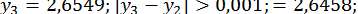
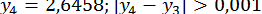 ;
;
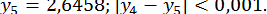
Отже, 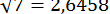 .
.
ПРИКЛАД 13. Обчислення кубічного кореня 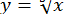 . Застосовуючи формулу (5) до функції
. Застосовуючи формулу (5) до функції 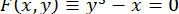 , отримуємо ітераційну формулу для обчислення кубічного кореня
, отримуємо ітераційну формулу для обчислення кубічного кореня
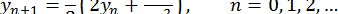
Використаємо її для обчислення 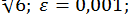
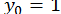 ;
;
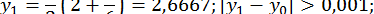
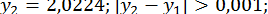
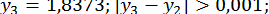
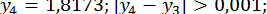
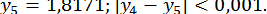
Отже, 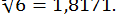
Задачі
1. Узагальнити схему Горнера для ділення многочлена 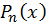 на квадратичний множник
на квадратичний множник 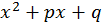 .
.
2. Обчислити з точністю до 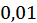 значення многочлена
значення многочлена
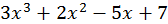 при
при 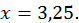
3. Обчислити з точністю до 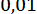 значення многочлена
значення многочлена
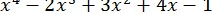 при
при 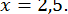
4. Обчислити з точністю до 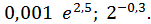
5. Обчислити з точністю до 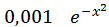 при
при 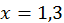 .
.
6. Обчислити з точністю до 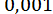
 при
при 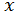 =0,4.
=0,4.
7. Вивести ітераційну формулу для обчислення оберненої величини квадратного кореня.
8. Обчислити 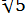 з точністю до
з точністю до 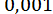 .
.
9. Обчислити 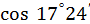 з точністю до
з точністю до 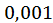 .
.
10. Скласти таблицю значень функції 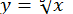 для
для
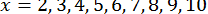 з точністю до
з точністю до 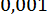 .
.
11. Обчислити 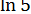 з точністю до
з точністю до 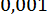 .
.
ЧИСЕЛЬНЕ РОЗВ’ЯЗАННЯ АЛГЕБРАЇЧНИХ ТА ТРАНСЦЕНДЕНТНИХ РІВНЯНЬ
Етап відділення коренів
Наближене знаходження коренів рівняння
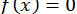 (6)
(6)
проводиться в два етапи: спочатку корені відділяються, тобто знаходяться відрізки заданої довжини, що містять лише один корінь рівняння, а потім початкові наближення коренів (будь-які значення із заданих відрізків) уточнюються тим чи іншим способом, поки не буде виконано нерівність
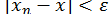 , де
, де 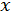 - корінь,
- корінь, 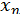 -
- 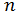 -е наближення до кореня,
-е наближення до кореня, 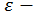 задана точність.
задана точність.
Нехай функція 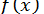 в рівнянні (6) неперервна в заданому інтервалі, і нехай рівняння (6) має лише ізольовані корені, та вимагається відокремити ці корені.
в рівнянні (6) неперервна в заданому інтервалі, і нехай рівняння (6) має лише ізольовані корені, та вимагається відокремити ці корені.
Аналітичний метод відділення коренів грунтується на наступній теоремі з аналізу:
Якщо неперервна на відрізку 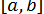 функція
функція 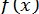 набуває значень різних знаків на кінцях відрізку, тобто
набуває значень різних знаків на кінцях відрізку, тобто 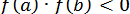 , то усередині цього відрізку міститься принаймні один корінь рівняння (6), тобто існує хоч би одне
, то усередині цього відрізку міститься принаймні один корінь рівняння (6), тобто існує хоч би одне 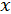 , таке що
, таке що 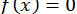 .
.
Для знаходження такого відрізку часто доводиться визначати знак функції 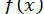 в досить великому числі точок.
в досить великому числі точок.
Зручнішим, як правило, виявляється графічний метод відділення коренів. Корені рівняння (6) є абсцисами точок перетину графіку функції 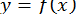 з віссю абсцис. Проте, часто буває вигідніше подати рівняння (6) у вигляді
з віссю абсцис. Проте, часто буває вигідніше подати рівняння (6) у вигляді
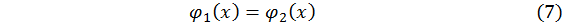
( 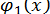 та
та 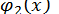 простіші, ніж
простіші, ніж 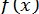 ) і знайти абсциси точок перетину кривих
) і знайти абсциси точок перетину кривих 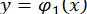 та
та 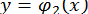 . Краще вказати відрізки, які містять абсциси точок перетину цих кривих.
. Краще вказати відрізки, які містять абсциси точок перетину цих кривих.
Практично надійніше поєднувати ці два методи. Спочатку зробити графічний рисунок, що показує розташування і число дійсних коренів, потім перевірити аналітичним методом, чи дійсно отримані з графіку відрізки містять корені цього рівняння. Річ у тому, що будувати графік з великою точністю недоцільно, а при малій точності графіку можливі помилки.
ПРИКЛАД 14. Відокремити корені рівняння
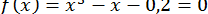
так, щоб довжина відрізку 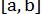 , що містить корінь, не перев ищувала
, що містить корінь, не перев ищувала  ; тобто
; тобто 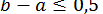 та
та 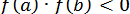 .
.
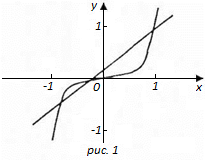
Рисунок 1 - Графіки функцій 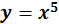 ;
; 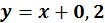
Зводимо рівняння до вигляду 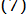 :
: 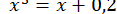 і будуємо графіки функцій
і будуємо графіки функцій 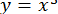 ;
; 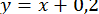 . На рис. 1 показано, що це рівняння має три дійсні корені, приблизно
. На рис. 1 показано, що це рівняння має три дійсні корені, приблизно 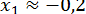 ;
; 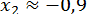 ;
; 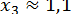 ; причом
; причом 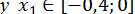 ;
; 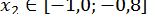 ;
; 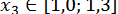 .
.
Дійсно,
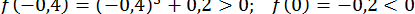 ;
;

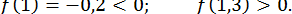
ПРИКЛАД 15. Відокремити корені рівняння

так, щоб 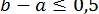 та
та 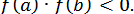
Побудувавши графіки функцій 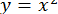 та
та 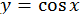 (рис. 2), бачимо, що рівняння має два корені
(рис. 2), бачимо, що рівняння має два корені 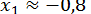 и
и 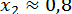 . Оскільки
. Оскільки 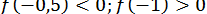 ;
; 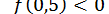 та
та 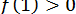 , то
, то 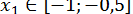 ;
; 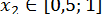 .
.
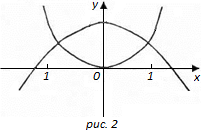
Рисунок 2 - Графіки функцій 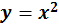 та
та 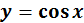
Помітимо, що в цьому прикладі в силу парності 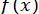 можна було обмежитися розглядом
можна було обмежитися розглядом 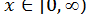 .
.
Існує ще один аналітичний метод відділення коренів. Він полягає в наступному. Для даного рівняння знаходиться простіше рівняння, яке має корені, що приблизно дорівнюють кореням початкового рівняння. Корені цього рівняння і будуть початковими наближеннями для коренів даного рівняння. Наприклад, нехай вимагається відокремити позитивний корінь рівняння
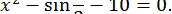
Можна помітити, що позитивний корінь цього рівняння близький до 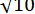 . Очевидно,
. Очевидно, 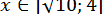 . Оскільки для
. Оскільки для 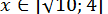 виконується нерівність
виконується нерівність 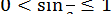 , то, замінюючи спочатку
, то, замінюючи спочатку 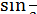 нулем, а потім - одиницею, отримуємо рівняння
нулем, а потім - одиницею, отримуємо рівняння 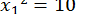 і
і 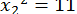 , між коренями яких розташований позитивний корінь цього рівняння, тобто
, між коренями яких розташований позитивний корінь цього рівняння, тобто 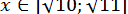 .
.
При відділенні коренів корисно враховувати різні особливості функції 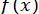 . Так, наприклад, очевидно, що алгебраїчне рівняння з позитивними коефіцієнтами не може мати позитивних коренів; корінь рівняння (6) в інтервалі
. Так, наприклад, очевидно, що алгебраїчне рівняння з позитивними коефіцієнтами не може мати позитивних коренів; корінь рівняння (6) в інтервалі 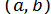 буде єдиним, якщо похідна
буде єдиним, якщо похідна 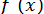 зберігає постійний знак на
зберігає постійний знак на 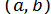 та ін.
та ін.
Задачі
Відокремити корені наведених нижче рівнянь так, щоб довжина відрізку, що містить корінь, не перевищувала  .
.
24. 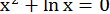 .
.
25. 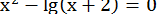 .
.
26. 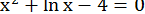 .
.
27. 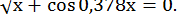
28.  .
.
29. 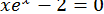 .
.
30.  .
.
31. 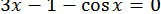 .
.
32. 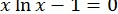 .
.
33. 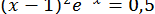 .
.
34. 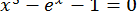 .
.
35.  .
.
36. 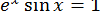 .
.
37. 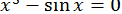 .
.
38. 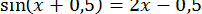 .
.
39. 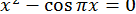 .
.
40. 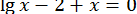 .
.
41. 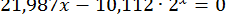 .
.
42. 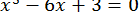 .
.
43. 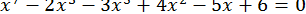 .
.
44. 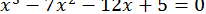 .
.
45. 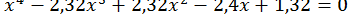 .
.
Дата: 2019-03-05, просмотров: 354.