Цель работы: познакомиться с явлением внутреннего трения в газах и основными газокинетическими характеристиками молекул.
Задача работы: экспериментальное определение длины свободного пробега и эффективного диаметра молекул воздуха по явлению внутреннего трения.
Теоретическая часть
В молекулярной физике мы часто имеем дело с такими физическими явлениями, как диффузия, теплопроводность, внутреннее трение. Теория этих явлений основана на понятиях средней длины свободного пробега и эффективного диаметра молекул газа. Рассмотрим эти понятия.
| Рис. 2-3.1. Траектория молекулы |
Выясним теперь, почему так происходит на примере идеального газа. Если бы частицы газа представляли материальные точки, они никогда бы не сталкивались друг с другом. Поэтому при рассмотрении столкновений молекул в газе их представляют в виде твердых шаров некоторого радиуса r. Столкновения между молекулами происходят всякий раз, когда центры двух молекул окажутся на расстоянии не больше, чем 2r друг от друга. На рис. 2-3.2 как раз изображен цилиндр радиусом 2r . Штриховая прямая представляет собой путь, по которому следовала бы одна из молекул, если бы она не испытывала столкновений. Столкновение произойдет, если центр другой молекулы окажется внутри этого цилиндра. Безусловно, как только произойдет столкновение, направление движения частицы изменится и вмести с ним изменится наш воображаемый цилиндр, но для упрощения вычислений мы не будем менять вид цилиндра. Предположим, что данная молекула – одна из многих, движущихся в газе со скоростью 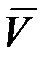 .
.
| V |
| 2r |
| r |
| V D t |
| Рис. 2-3.2. Столкновения частиц |
Представим себе на мгновение, что другие молекулы не движутся и, что концентрация молекул равна n . Тогда число молекул, центры которых лежат внутри цилиндра, определится как концентрация n , умноженная на объем этого цилиндра. Это число будет равно также и числу произошедших столкновений, обозначим его z. За промежуток времени 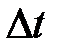 молекула пройдет расстояние
молекула пройдет расстояние 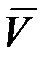
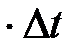 , в этом случае объем цилиндра равен π (2r)2
, в этом случае объем цилиндра равен π (2r)2 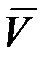
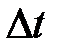 (рис. 2-3.2). Таким образом, число столкновений z за время
(рис. 2-3.2). Таким образом, число столкновений z за время 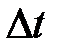 равно n π (2r)2
равно n π (2r)2 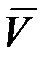
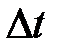 . Мы определили среднюю длину свободного пробега l как среднее расстояние между столкновениями; это расстояние равно расстоянию, пройденному за время
. Мы определили среднюю длину свободного пробега l как среднее расстояние между столкновениями; это расстояние равно расстоянию, пройденному за время 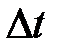 , деленному на число столкновений, произошедших за время
, деленному на число столкновений, произошедших за время 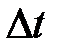 :
:
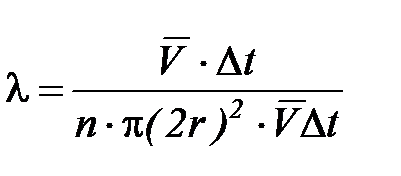 . (2-3.1)
. (2-3.1)
Однако выражение (2-3.1) является не совсем точным, поскольку мы предположили, что остальные молекулы неподвижны. В действительности они движутся, и число столкновений за время 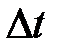 должно зависеть от относительной скорости сталкивающихся молекул, а не от
должно зависеть от относительной скорости сталкивающихся молекул, а не от 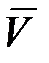 . Следовательно, число столкновений в секунду равно n π (2r)2
. Следовательно, число столкновений в секунду равно n π (2r)2 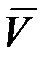 отн
отн 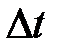 , где
, где 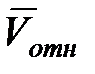 – средняя относительная скорость сталкивающихся молекул. Максвелл, используя функцию распределения молекул по скоростям, показал, что
– средняя относительная скорость сталкивающихся молекул. Максвелл, используя функцию распределения молекул по скоростям, показал, что
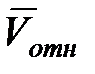 .=
.= 
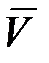 [1] *.
[1] *.
Следовательно, средняя длина свободного пробега в уравнении (1) принимает вид
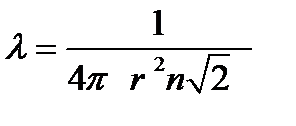 . (2-3.2)
. (2-3.2)
Как видно из последнего выражения, средняя длина свободного пробега зависит от концентрации молекул газа. Если воспользоваться основным уравнением молекулярно кинетической теории идеального газа и записать n = P / kT , то из выражения
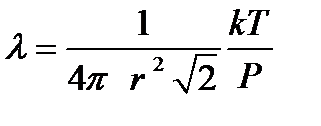 . .
| (2-3.3) |
| d |
| Рис. 2-3.3. Эффективный диаметр молекулы |
Выше мы отмечали, что молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 2-3.3.).
Величина σ = π d 2 также является важной характеристикой при изучении кинематического движения частиц и называется эффективным сечением молекулы. Тогда выражение (2-3.3) может быть представлено в форме 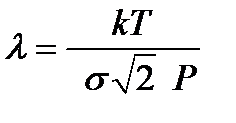 . Откуда
. Откуда
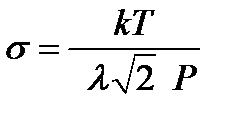 . (2-3.4)
. (2-3.4)
При нормальных условиях n ~1025 средняя длина свободного пробега молекул воздуха равна 10 –6м, в то время как диаметр молекул N2 и O2 имеет порядок приблизительно 10-10 м. Рассматриваются только парные столкновения. Случаи, когда в реальных газах сближаются и начинают взаимодействовать три молекулы и больше, маловероятны и по этой причине не принимаются во внимание. Хотя эффективное сечение σ представлено здесь в геометрическом смысле, оно несколько уменьшается с повышением температуры. Объяснение этому было дано Сезерлендом [2]: σ= σ0(1+С/T), где С – постоянная, называемая постоянной Сезерленда, имеет размерность температуры. Он использовал модель твердых шаров, но учел силы притяжения, с которыми молекулы действуют друг на друга в промежутках между столкновениями. С ростом температуры молекула несколько меньше времени находится в поле влияния другой молекулы и пролетает мимо нее без «захвата», что и приводит к увеличению длины свободного пробега молекул. Поэтому эффективное сечение у одних и тех же частиц для различных процессов может быть различным.
| P1 |
| P2 |
| X |
| Рис. 2-3.4. Механизм возникновения вязкости |
Одним из способов определения длины свободного пробега и эффективного диаметра молекул газа является определение этих характеристик с использованием явления внутреннего трения. Представим себе, что газ протекает по трубе цилиндрического сечения. Скорости отдельных слоев в потоке различны: с наибольшей скоростью движется слой газа в средней части капилляра, а по мере приближения к стенкам скорость убывает, у самой стенки имеется слой газа с нулевой скоростью, так как молекулы газа абсорбируются поверхностью (прилипают к ней) (рис. 2-3.4).Таким образом, поперек направления движения наблюдается градиент скорости движущихся слоев газа. Для поддержания движения газа по трубе необходимо создать разность давлений на ее концах. Однако в результате теплового движения молекулы, перемещаясь из более быстрого слоя в более медленный и обратно, переносят при этом импульс и при столкновениях друг с другом обмениваются импульсами. В результате скорость направленного движения быстро движущегося слоя уменьшается, а медленно движущегося слоя – увеличивается. На границе раздела слоев возникают силы внутреннего трения. Необходимо помнить, что силы вязкости являются тангенциальными силами, т.е. направлены вдоль поверхности соприкасающихся слоев.
Тогда поток импульса через единицу площади DS границы раздела двух слоев газа определяется величиной градиента скорости 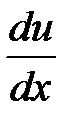
| K |
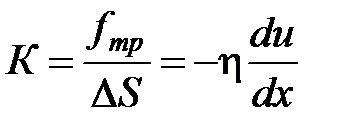 , где h – коэффициент внутреннего трения или динамической вязкости. Знак «минус» означает, что поток импульса и вектор градиента скорости направлены в противоположные стороны.
, где h – коэффициент внутреннего трения или динамической вязкости. Знак «минус» означает, что поток импульса и вектор градиента скорости направлены в противоположные стороны.
Величина η определяется соотношением
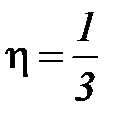 λ λ 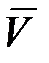 ρ, ρ,
| (2-3.5) |
где ρ -плотность газа, λ -средняя длина свободного пробега молекул, 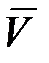 - средняя скорость молекул.
- средняя скорость молекул.
Коэффициент внутреннего трения η, как показывает молекулярно-кинетическая теория, в широких пределах от давления не зависит, так как плотность газа пропорциональна давлению, а длина свободного пробега обратно пропорциональна ему. Единицей динамической вязкости в СИ является Па с (Пуаз), т.е. это вязкость такого газа, у которого при площади соприкосновения слоев 1 м2 при градиенте скорости 1 м/с возникает сила внутреннего трения, равная 1 Н (1Пз = 0,1 Н с/м2).
При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется – возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. Ламинарным или турбулентным является движение жидкости или газа в зависимости от того, насколько значительную роль играют силы трения. Английский ученый Рейнольдс установил критерий (число Рейнольдса Rе), по которому ламинарное течение переходит в турбулентное. Число Rе характеризует относительную роль сил вязкости, т.к. оно характеризует отношение кинетической энергии движения элемента жидкости к потере ее, обусловленной работой сил вязкости. Таким образом, число Рейнольдса определяет относительную роль инерции и вязкости жидкости при течении. Чем меньше число Рейнольдса, тем большую роль играют силы вязкости в движении жидкости или газа. При значениях числа Rе<1000 – течение, как правило, носит ламинарный характер. При бόльших значениях числа Рейнольдса течение приобретает турбулентный характер, заметим, что турбулентность в гладких трубах наступает при значении Reкр~1160.
Итак, в данной задаче требуется определить газокинетические характеристики молекул воздуха: длину свободного пробега и эффективный диаметр по коэффициенту внутреннего трения в газах. При ламинарном течении газа по капилляру, т.е. течении, при котором различные слои газа текут хотя и с разными скоростями, но параллельно друг другу, справедлива формула Пуазейля . Объем газа, протекающего при стационарном течении через капилляр за время t:

| (2-3.6) |
где r - радиус капилляра, 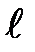 - его длина, D P - разность давлений на концах капилляра. Откуда следует выражение для коэффициента вязкости:
- его длина, D P - разность давлений на концах капилляра. Откуда следует выражение для коэффициента вязкости:
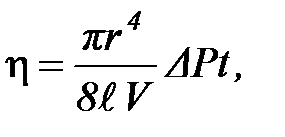
| (2-3.7) |
Исходя из выражения (5), можно определить среднее значение длины свободного пробега, т.е.
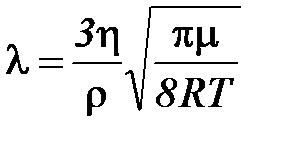 и и 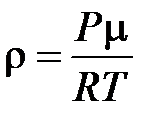 , ,
| (2-3.8) |
где Р - давление воздуха в помещении, определяемое по барометру, Т -температура воздуха в градусах Кельвина.
Из выражения (4) можно найти эффективное сечение, а затем и эффективный диаметр молекул воздуха.
Экспериментальная часть
Дата: 2019-03-05, просмотров: 528.