Фильтр — это система или сеть, избирательно меняющая форму сигнала (амплитудно-частотную или фазово-частотную характеристику). Основными целями фильтрации являются улучшение качества сигнала (например, устранение или снижение помех), извлечение из сигналов информации или разделение нескольких сигналов, объединенных ранее для, например, эффективного использования доступного канала связи.

Термином цифровой фильтр называют аппаратную или программную реализацию математического алгоритма, входом которого является цифровой сигнал, а выходом — другой цифровой сигнал, форма которого и/или амплитудная и фазовая характеристики специальным образом модифицированы. Во многих приложениях цифровые фильтры предпочтительнее аналоговых, поскольку они позволяют более точно воплотить амплитудные и фазовые спецификации. Кроме того, для цифровых фильтров нехарактерно присущее аналоговым фильтрам изменение характеристик в зависимости от температуры и напряжения.

Ключевые особенности КИХ-фильтров

1. Стандартный КИХ-фильтр характеризуется следующими уравнениями:

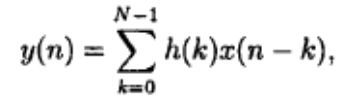(7.1, а) и 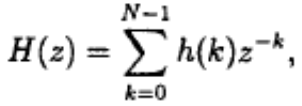(7.1, б)

где h(k), k=0, 1, ..., N-1 — коэффициенты импульсной характеристики, H(z) — передаточная функция фильтра, а N — длина фильтра, т.е. число коэффициентов фильтра. Формула (7.1, а) — это разностное уравнение КИХ-фильтра. Данное уравнение записано во временной области и представляет КИХ-фильтр в его нерекурсивной форме: текущая выходная выборка у(n) — это функция только текущего и прошедших значений на входе х(n). При реализации КИХ-фильтров в такой форме, т.е. через прямое представление формулы (7.1, а), фильтры всегда устойчивы. В формуле (7.1, б) записана передаточная функция фильтра, нужная для анализа фильтра, например, расчета частотной характеристики.

2. КИХ-фильтры могут иметь точную линейную фазовую характеристику.

3. КИХ-фильтры очень просто реализовать. Архитектура всех существующих процессоров ЦОС подходит для фильтрации с конечной импульсной характеристикой. Кроме того, нерекурсивные КИХ-фильтры менее подвержены эффектам конечной разрядности, чем БИХ-фильтры. Существуют также рекурсивные КИХ-фильтры, использование которых иногда вычислительно выгоднее.

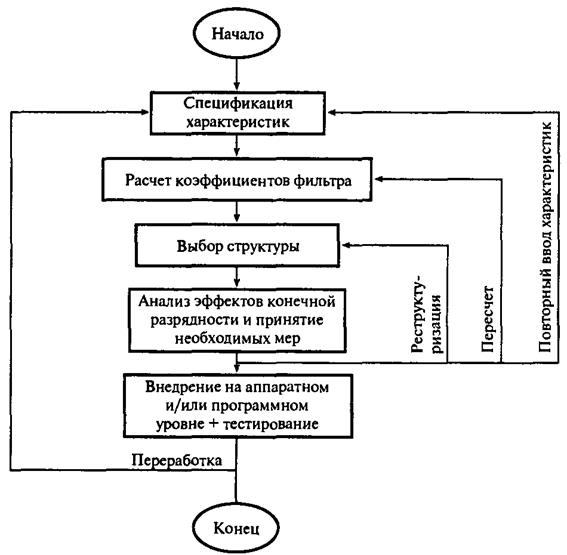
Разработка КИХ-фильтров

1. Спецификация фильтра. На данном этапе может задаваться тип фильтра, например, фильтр нижних частот, нужная амплитудная и/или фазовая характеристика и разрешенные допуски (если есть), частота дискретизации и длина слов, которыми будут представлены входные данные.

2. Вычисление коэффициентов. На этом этапе определяются коэффициенты передаточной функции H(z), которая удовлетворяет спецификациям, полученным на этапе 1. На выбор метода расчета коэффициентов влияет несколько факторов, важнейшими из которых являются критические требования, сформулированные на этапе 1.

3. Выбор структуры. Данный этап включает преобразование передаточной функции, полученной на предыдущем этапе, в подходящую фильтрующую структуру или сеть.

4. Анализ следствий конечной разрядности. Здесь оценивается влияние квантования на коэффициенты фильтра и входные данные, а также влияние на производительность фильтра операции фильтрации со словами конечной длины.

5. Воплощение. На данном этапе разрабатывается программный код и/или аппаратный блок и выполняется собственно фильтрация.

Единственной целью большинства методов вычисления (или приближенного вычисления) коэффициентов КИХ-фильтров является получение значений h(n), при которых фильтр удовлетворяет спецификациям, в частности, относящимся к амплитудно-частотной характеристике, и требованиям к пропускной способности. Разработано несколько методов получения h(n). Наиболее широко используемыми из них являются метод вырезания, оптимальный метод и метод частотной выборки. Все три метода позволяют получать КИХ-фильтры с линейной фазовой характеристикой.

Метод взвешивания прост, но ему недостает гибкости, особенно при наличии разных амплитуд колебаний характеристики в полосе пропускания и подавления. Метод частотной выборки великолепно подходит для рекурсивной реализации КИХ-фильтров и в тех случаях, когда требуются фильтры, отличные от стандартных частотно-избирательных фильтров (нижних частот, верхних частот, полосовых и режекторных). Оптимизационный метод наиболее мощный и гибкий.