Любой периодический сигнал f(t) можно представить в виде суммы бесконечного числа синусоидальных и косинусоидальных членов и одного постоянного члена. Это представление называется рядом Фурье и задается следующим образом:

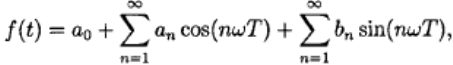(3.1)

где t — независимая переменная, которая часто обозначает время, но может обозначать, например, расстояние или любую другую величину; f(t) часто обозначает функцию зависимости напряжения от времени, но может обозначать и любой сигнал, ω=2π/T_p называют циклической частотой первой (или основной) гармоники, связанной с основной частотой f соотношением ω=2πf, Т_р — период повторения сигнала, через

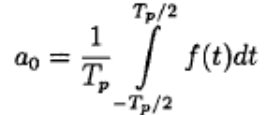обозначается постоянная, равная усредненному по времени сигналу f(t) за один период, которая может представлять, например, уровень постоянного напряжения,

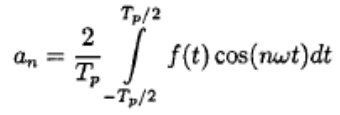 и

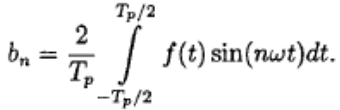
Частоты nω называют n-ми гармониками частоты ω. Следовательно, бесконечный ряд (3.1) содержит зависящие от частоты синусоидальные и косинусоидальные члены с различными амплитудами а_n и b_n на положительных частотах гармоник nω. Этот ряд можно записать компактнее с помощью экспоненциального представления, кроме того, в таком виде намного упрощается выполнение математических операций. Итак, в экспоненциальной форме ряд Фурье выглядит так:

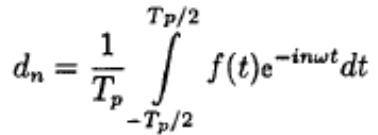(3.2), где (3.3)

являются комплексными числами, a |d_n| — величины, измеряемые в вольтах.

При суммировании учитываются и отрицательные значения n, так что половину ряда составляют отрицательные частоты -nω. Они не имеют физического значения и являются чисто математическим понятием, но вследствие этого модули |d_n| комплексных амплитуд d_n численно уменьшены в два раза. Это означает равное распределение амплитуды по соответствующим отрицательной и положительной частотам. Следовательно, правильное значение амплитуды на частоте nω можно найти, удвоив рассчитанную величину. Комплексная и тригонометрическая формы связаны следующими соотношениями:

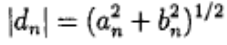(3.4) и 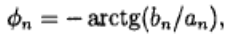(3.5)

где ф_n — сдвиг фазы компонента n-й гармоники, который также задается как арктангенс отношения мнимой и действительной частей d_n. Следовательно, каждая гармоника сигнала характеризуется своим фазовым сдвигом и амплитудой.

Спектр сигнала

Дискретные преобразования позволяют описывать сигналы с дискретным временем в частотных координатах или переходить от описания во временной области к описанию в частотной. Для получения спектра сигнал раскладывается на частотные составляющие с помощью дискретного преобразования. Знание такого спектра неоценимо, например, при определении ширины полосы, что необходимо для передачи сигнала. Переход от временных координат к частотным необходим во многих приложениях ЦОС. Например, он позволяет более эффективно реализовывать такие алгоритмы ЦОС, как цифровая фильтрация, свертка и корреляция.