Фильтр — это система или сеть, избирательно меняющая форму сигнала (амплитудно-частотную или фазово-частотную характеристику). Основными целями фильтрации являются улучшение качества сигнала (например, устранение или снижение помех), извлечение из сигналов информации или разделение нескольких сигналов, объединенных ранее для, например, эффективного использования доступного канала связи.

Термином цифровой фильтр называют аппаратную или программную реализацию математического алгоритма, входом которого является цифровой сигнал, а выходом — другой цифровой сигнал, форма которого и/или амплитудная и фазовая характеристики специальным образом модифицированы. Во многих приложениях цифровые фильтры предпочтительнее аналоговых, поскольку они позволяют более точно воплотить амплитудные и фазовые спецификации. Кроме того, для цифровых фильтров нехарактерно присущее аналоговым фильтрам изменение характеристик в зависимости от температуры и напряжения.

Выбор между КИХ- и БИХ-фильтрами

1. КИХ-фильтры могут иметь строго линейную фазовую характеристику. Следовательно, фильтр не вводит фазового искажения в сигнал, что важно во многих сферах, например, передаче данных, биомедицине, цифровой аудиообработке или обработке изображений. Фазовая характеристика БИХ-фильтров нелинейна, особенно на краях полос.

2. КИХ-фильтры реализованы нерекурсивно, т.е. они всегда устойчивы. Гарантировать устойчивость БИХ-фильтров удается не всегда.

3. Для реализации фильтров используется ограниченное число битов. Практические последствия этого (например, шум округления и ошибки квантования) значительно менее существенны для КИХ-фильтров, чем для БИХ-фильтров.

4. Чтобы получить конечную импульсную характеристику с помощью фильтров с резкими срезами характеристики, потребуется больше коэффициентов, чем для получения бесконечной импульсной характеристики. Следовательно, для реализации предложенной спецификации амплитудной характеристики с КИХ необходимо больше вычислительной мощности и памяти, чем для реализации ее с БИХ. Впрочем, эффективность КИХ-реализаций можно значительно повысить, сыграв на вычислительной скорости БПФ и обработке при нескольких скоростях.

5. Аналоговые фильтры легко преобразовать в эквивалентные цифровые БИХ-фильтры, удовлетворяющие сходным спецификациям. Для получения КИХ-фильтров такое преобразование невозможно, поскольку для них не существует аналоговых прототипов. Впрочем, получать произвольные частотные характеристики на КИХ-фильтрах легче.

6. Вообще, синтез КИХ-фильтров алгебраически сложнее, если не использовать компьютерную поддержку разработки.

7. БИХ-фильтры рекуррентны. Это означает, что, пропустив через фильтр один и тот же сигнал, но с “обратным ходом времени”, мы получим, вообще говоря, разные результаты. Если для речи временная анизотропия естественна, то, например, для изображений уже нет, поэтому БИХ-фильтры имеют ряд ограничений по применению.

Основные характеристики БИХ-фильтров

Реальные цифровые БИХ-фильтры характеризуются следующим рекурсивным уравнением:

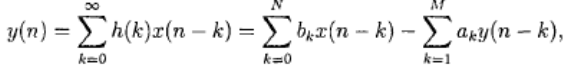(8.1)

где h(k) — импульсная характеристика фильтра, длительность которой теоретически бесконечна, b_k и а_k — коэффициенты фильтра, х(n) и у(n) — вход и выход фильтра. Передаточная функция БИХ-фильтра записывается следующим образом:

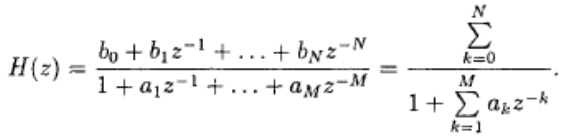(8.2)

Важной составляющей процесса разработки БИХ-фильтра является поиск таких значений коэффициентов b_k и а_k, чтобы определенные аспекты характеристик фильтра, например, частотная характеристика, вели себя определенным образом. Уравнения БИХ-фильтров приведены в формулах (8.1) и (8.2).

В уравнении (8.1) текущая выходная выборка у(n) является функцией прошедших выходов у(n-k), а также текущей и прошедших входных выборок х(n-k), т.е. БИХ-фильтр — это определенная система с обратной связью. Достоинства БИХ-фильтров объясняются именно гибкостью, которую обеспечивает обратная связь. Например, БИХ-фильтр обычно требует меньше коэффициентов, чем КИХ-фильтр при идентичном наборе спецификаций, поэтому БИХ-фильтры используются тогда, когда важны резкие срезы характеристики. Ценой этого является потенциальная неустойчивость БИХ-фильтра, кроме того, если при разработке не принять надлежащих мер, возможно значительное снижение производительности.

Передаточную функцию БИХ-фильтра Н(z), представленную в формуле (8.2), можно факторизовать следующим образом:

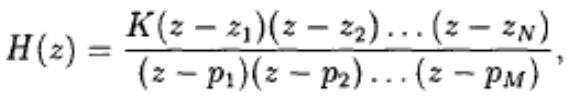(8.3)

где z₁,z₂, ... — нули H(z), т.е. те значения z, при которых H(z) становится равной нулю, a p₁, p₂, … — полюса H(z), т.е. значения z, при которых H(z) бесконечна.

График полюсов и нулей передаточной функции называется диаграммой нулей и полюсов и является удобным средством представления и анализа фильтра на комплексной плоскости. Чтобы фильтр был устойчивым, все его полюса должны лежать внутри единичной окружности (или совпадать с нулями на единичной окружности). На положения нулей ограничений не существует.

Этапы разработки цифровых БИХ-фильтров

1. Составление спецификации фильтра, в которой разработчик задает передаточную функцию фильтра (например, указывает, что требуется фильтр нижних частот) и желаемую производительность.

2. Аппроксимация или расчет коэффициентов, когда выбирается один из доступных методов и вычисляются значения коэффициентов b_k и а_k, передаточной функции H(z), которая соответствует спецификациям, предложенным на этапе 1.

3. Выбор подходящей фильтрующей структуры, в которую переводится передаточная функция. Обычно в БИХ-фильтрах используются параллельная структура и/или каскады блоков второго и/или первого порядка.

4. Анализ ошибок, которые могут появиться при представлении коэффициентов фильтра и выполнении арифметических операций, фигурирующих при фильтрации, с помощью конечного числа битов.

5. Реализация, которая включает построение аппаратного обеспечения и/или написание программного кода плюс выполнение собственно фильтрации.

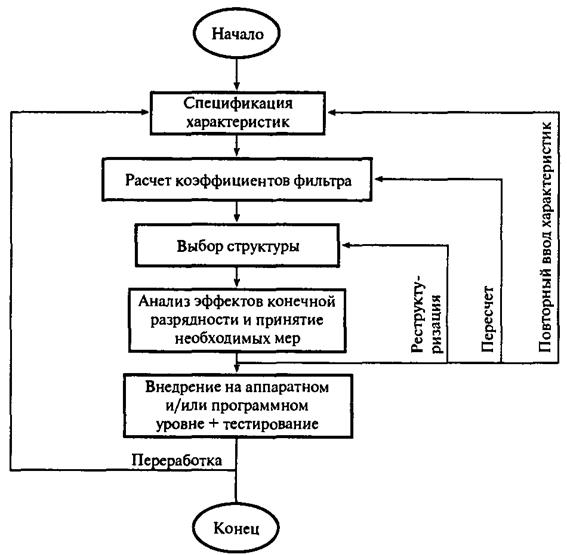
Пять этапов не являются независимыми, и они не всегда выполняются в указанном порядке. Фактически существуют методы, в которых второй, третий и четвертый этапы объединены. В то же время описанный подход гарантирует успешный результат, иногда, правда, для этого требуется несколько итераций, в ходе которых повторяется один или несколько этапов.

Методы расчета коэффициентов БИХ-фильтров

На этом этапе вначале выбирается метод аппроксимации, который затем используется для расчета значений коэффициентов а_k и b_k в уравнении (8.2), при которых спецификации частотной характеристики, полученные на первом этапе разработки, будут удовлетворены.

Для простого получения коэффициентов БИХ-фильтра можно разумно разместить полюса и нули на комплексной плоскости, чтобы получающийся в результате фильтр имел нужную частотную характеристику. Данный подход, известный как метод размещения нулей и полюсов, полезен только при разработке простых фильтров, например, узкополосных режекторных фильтров, где параметры фильтра (такие как неравномерность в полосе пропускания) не обязательно задавать точно. Более эффективный подход — вначале разработать аналоговый фильтр, удовлетворяющий желаемой спецификации, а затем преобразовать его в эквивалентный цифровой. Большинство цифровых БИХ-фильтров разрабатываются именно так. Данный подход получил широкое распространение потому, что на настоящий момент в литературе имеется масса информации по аналоговым фильтрам, которую можно использовать при разработке цифровых фильтров. Тремя наиболее распространенными методами конвертации аналоговых фильтров в эквивалентные цифровые являются метод инвариантного преобразования импульсной характеристики, согласованное z -преобразование и билинейное z -преобразование.

15. Применение быстрого преобразования Фурье при спектральном анализе и фильтрации.

1. При спектральном анализе

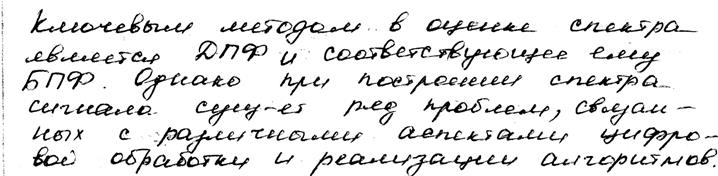
Существуют различные методы оценки спектра. Их можно разделить на 2 группы – параметрические и непараметрические.

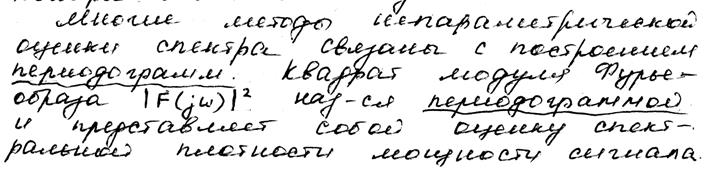
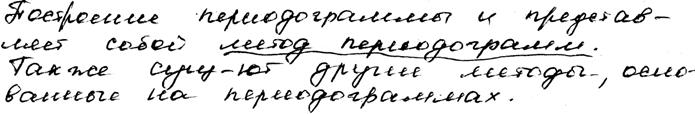
2. При фильтрации