Розглянемо функцію 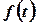 дійсної змінної
дійсної змінної 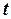 , яка відповідає таким умовам:
, яка відповідає таким умовам:
1. При 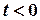
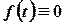 .
.
2. При 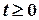 функція
функція 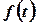 на будь-якому скінченному проміжку вісі
на будь-якому скінченному проміжку вісі 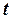 має не більше ніж скінченну кількість точок розриву першого роду.
має не більше ніж скінченну кількість точок розриву першого роду.
3. При 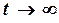 функція
функція 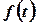 має обмежену степінь зростання, тобто існують такі додатні константи
має обмежену степінь зростання, тобто існують такі додатні константи 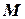 та
та 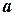 , що для всіх
, що для всіх 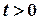
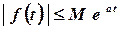 .
.
Інтегральне перетворення Лапласа ставить у відповідність такій функції
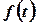 функцію
функцію 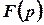 комплексної змінної
комплексної змінної 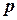 за допомогою співвідношення
за допомогою співвідношення
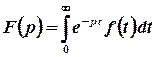 .
.
Функція 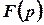 називається зображенням Лапласа функції
називається зображенням Лапласа функції 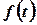 , а функція
, а функція 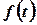 – оригіналом функції
– оригіналом функції 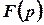 . Зв’язок між функціями
. Зв’язок між функціями 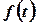 та
та 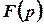 будемо символічно позначати таким чином:
будемо символічно позначати таким чином:
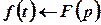 .
.
Основні властивості інтегрального перетворення Лапласа.

1. Лінійність зображення 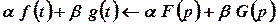 .
.
2. Теорема подібності 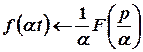 .
.
3. Диференціювання оригіналу 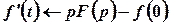 ;
;
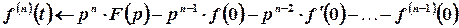 .
.
4. Диференціювання зображення 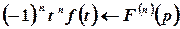 .
.
5. Інтегрування оригіналу 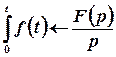
6. Інтегрування зображення 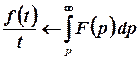 .
.
7. Теорема спізнення 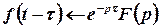 .
.
8. Теорема зміщення 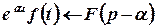
9. Теорема множення (теорема Бореля) 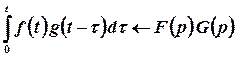 .
.
Зображення Лапласа деяких функцій
Перетворення Лапласа застосовується для функцій, які при від’ємному значенні аргумента дорівнюють нулю. Такі функції можуть бути записані у вигляді 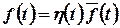 , де
, де 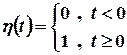 – функція Хевісайда, а
– функція Хевісайда, а 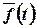 – деяка функція. У подальшому будемо у більшості випадків випускати множник
– деяка функція. У подальшому будемо у більшості випадків випускати множник 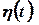 , маючи на увазі його наявність.
, маючи на увазі його наявність.
Наведемо зображення Лапласа функцій, які найчастіше зустрічаються при розв’язуванні нескладних задач.
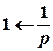 ;
; 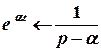 ;
;
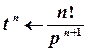 ;
; 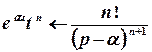 ;
;
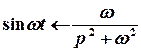 ;
; 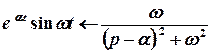 ;
;
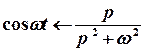 ;
; 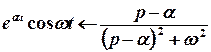 .
.
Існують спеціальні таблиці зображень елементарних та спеціальних функцій, які наведені у посібниках з інтегральних перетворень та довідниках .
Якщо функція 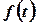 є кусочно неперервною, наприклад, має вигляд
є кусочно неперервною, наприклад, має вигляд 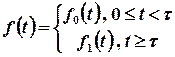 , її можна записати за допомогою функції Хевісайда у вигляді
, її можна записати за допомогою функції Хевісайда у вигляді 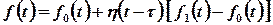 , або
, або 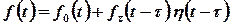 . Тоді відповідне зображення має вигляд
. Тоді відповідне зображення має вигляд 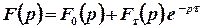 . Зокрема, зображенням функції
. Зокрема, зображенням функції 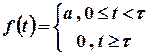 буде
буде 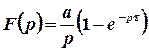 .
.
Визначення оригіналу за відомим зображенням
Якщо відомо, що задана функція 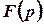 в області
в області 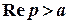 є зображенням кусочно гладкої функції
є зображенням кусочно гладкої функції 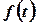 , степінь зростання якої не перевищує
, степінь зростання якої не перевищує 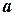 , то
, то
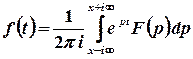 ,
, 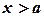 .
.
Наведена рівність називається формулою Мелліна.
Якщо функція 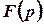 є правильним раціональним дробом, то її оригінал можна побудувати за формулою
є правильним раціональним дробом, то її оригінал можна побудувати за формулою
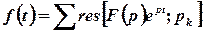 .
.
Зокрема, якщо всі полюси функції 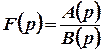 є простими, то
є простими, то
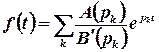 ,
,
причому, якщо серед полюсів є комплексно спряжені, то формула набуває вигляду
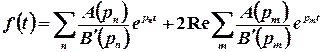 ,
,
де 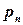 – дійсні полюси, а
– дійсні полюси, а 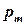 – комплексні полюси з додатною уявною частиною.
– комплексні полюси з додатною уявною частиною.
Дуже важливим з практичної точки зору є також відшукування оригіналу методом підбору: записують зображення у вигляді суми функцій, оригінали яких відомі, та представляють шуканий оригінал як суму цих оригіналів.
КОНТРОЛЬНА РОБОТА № 7
Тема 1. Теорія функцій комплексної змінної
Література : [1], гл. I-VII; [2], гл. 1, § 1-6, гл. 2, гл. 4,гл. 5, § 1; [3], гл. I;
[6], гл. 11, § 1, 2, 4, гл. 12, § 1, 3, 5, 6.
При вивченні матеріалу цієї теми студент повинен усвідомити основні поняття теорії функції комплексної змінної , навчитися обчислювати значення елементарних функцій, інтегралів вздовж замкненого контуру, будувати розвинення функцій в ряд Лорана та обчислювати лишки.
Розглянемо приклади.
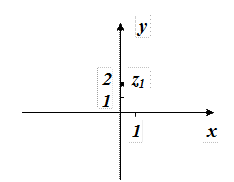
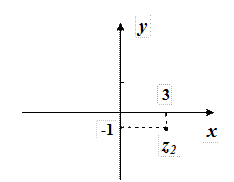
Приклад 1. Побудувати на комплексній площині числа 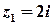 ,
, 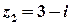 .
.
Розв’язок. Числу 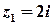 на координатній площині відповідає точка з координатами
на координатній площині відповідає точка з координатами 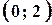 , а числу
, а числу 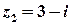 – точка
– точка 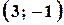 .
.
Приклад 2. Виконати арифметичні дії з комплексними числами 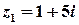 ,
, 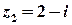 .
.
Розв’язок. 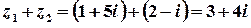 ;
;
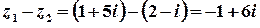 ;
;
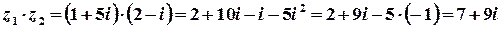 ;
;
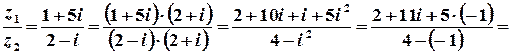
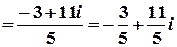 .
.
Приклад 3. Записати комплексні числа у показниковій та тригонометричній формах.
а) 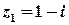 .
.
Розв’язок. Обчислимо модуль та головне значення аргумента комплексного числа.
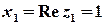 ,
, 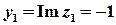 .
.
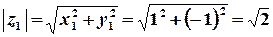 ;
;
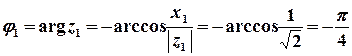 , або
, або
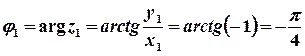 .
.
Тоді 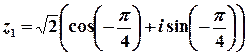 – тригонометрична форма,
– тригонометрична форма,
та 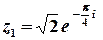 – показникова форма.
– показникова форма.
б) 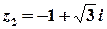 .
.
Розв’язок. 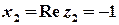 ,
, 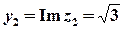 ;
;
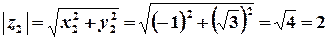 ;
;
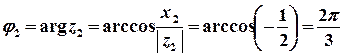 , або
, або
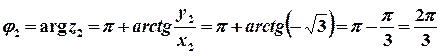 .
.
Тоді 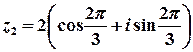 – тригонометрична форма,
– тригонометрична форма,
та 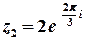 – показникова форма.
– показникова форма.
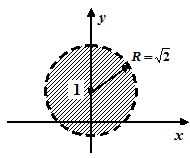
Приклад 4. Зобразити геометричне місце точок, які задовольняють умові
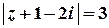 .
.
Розв’язок.
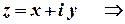
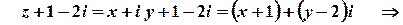
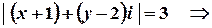
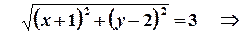
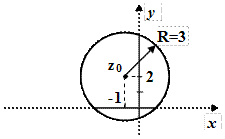
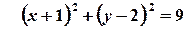 .
.
Це рівняння кола з центром у точці 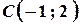 , яка відповідає комплексному числу
, яка відповідає комплексному числу 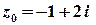 . Радіус кола дорівнює
. Радіус кола дорівнює 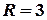 .
.
Приклад 5. Обчислити значення функцій комплексної змінної.
а) 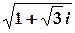 .
.
Розв’язок. Обчислимо модуль та головне значення аргументу комплексного числа.
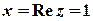 ,
, 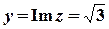 ;
; 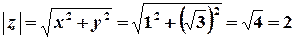 ;
;
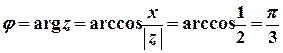 .
.
Тоді 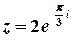 . За правилом обчислення кореня з комплексного числа маємо
. За правилом обчислення кореня з комплексного числа маємо
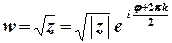 ,
, 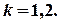
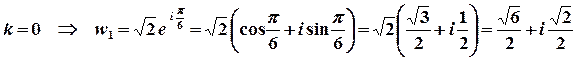
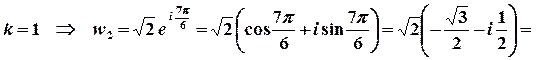
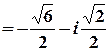 .
.
б) 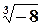 .
.
Розв’язок. 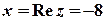 ,
, 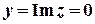 ;
; 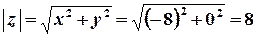 ;
;
 .
.
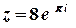 .
.
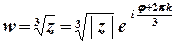 ,
, 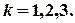
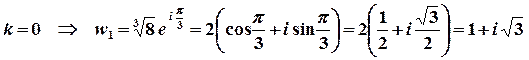
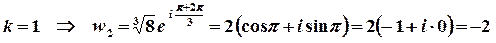
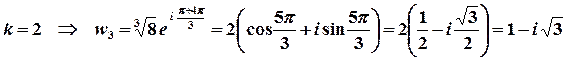 .
.
в) 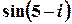 .
.
Розв’язок.
1 спосіб. Значення синуса комплексного аргумента можна обчислити з використанням зв’язку цієї тригонометричної та показникової функції.
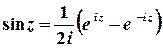 ;
;
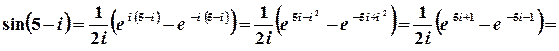
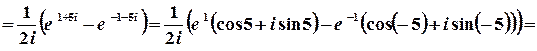
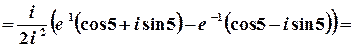
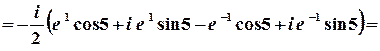
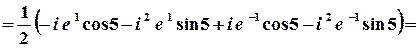
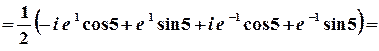
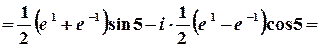
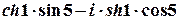 .
.
2 спосіб. Для тригонометричних функцій комплексної змінної є вірними всі властивості функцій дійсної змінної.
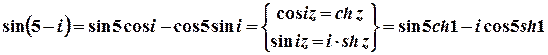 .
.
г) 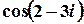 .
.
Розв’язок.
1 спосіб. 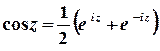
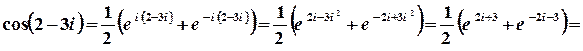
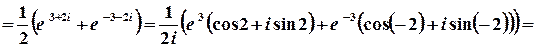
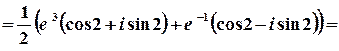
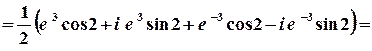
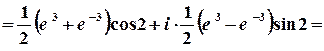
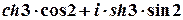 .
.
2 спосіб.
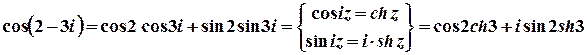 .
.
д) 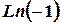 .
.
Розв’язок. 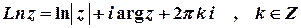 .
.
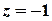 ,
, 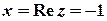 ,
, 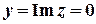 ,
, 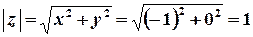 ;
;
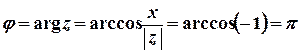 ;
;
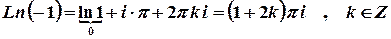 .
.
е) 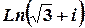 .
.
Розв’язок. 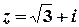 ,
, 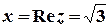 ,
, 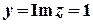 ,
, 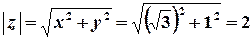 ;
; 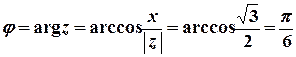 ;
;
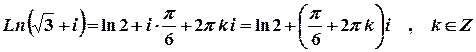 .
.
Приклад 6. З’ясувати, чи є функція 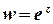 аналітичною.
аналітичною.
Розв’язок. 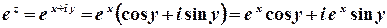 .
.
Отже, 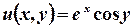 ;
; 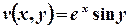 .
.
Обчислимо частинні похідні цих функцій.
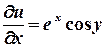 ;
; 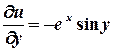 ;
;
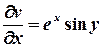 ;
; 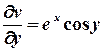 .
.
Умови Коші – Рімана 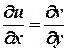 ,
, 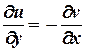 виконуються для будь-яких дійсних х та у , отже, функція
виконуються для будь-яких дійсних х та у , отже, функція 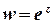 є аналітичною на всій комплексній площині.
є аналітичною на всій комплексній площині.
Приклад 7. Обчислити інтеграли по замкнутому контуру.
а) 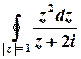 .
.
Розв’язок. Функція 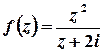 аналітична на всій комплексній площині, крім точки
аналітична на всій комплексній площині, крім точки 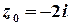 .
.
Побудуємо контур інтегрування – коло 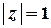 .
.
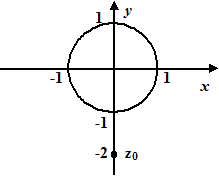 Точка
Точка 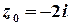 розташована поза колом
розташована поза колом 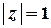 , тому
, тому 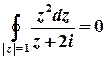
б) 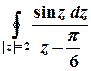 .
.
Розв’язок. Функція 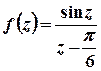 аналітична на всій комплексній площині, крім точки
аналітична на всій комплексній площині, крім точки 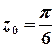 .
.
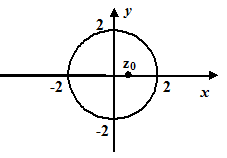 Побудуємо контур інтегрування – коло
Побудуємо контур інтегрування – коло 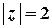 . Точка
. Точка 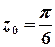 – внутрішня точка цього кола, функція
– внутрішня точка цього кола, функція 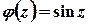 аналітична, тому за інтегральною формулою Коші
аналітична, тому за інтегральною формулою Коші
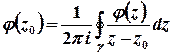
(або 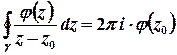 ) отримаємо
) отримаємо
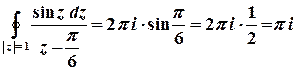 .
.
в) 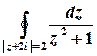 .
.
Розв’язок. Функція 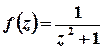 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 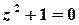 , тобто крім точок
, тобто крім точок 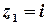 та
та 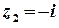 .
.
Побудуємо контур інтегрування – лінію 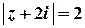 . Це коло з центром в точці
. Це коло з центром в точці 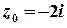 та радіусом
та радіусом 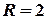 .
.
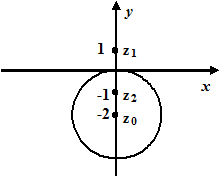 Точка
Точка 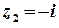 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 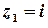 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 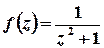 можна записати у вигляді
можна записати у вигляді 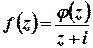 , де
, де 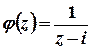 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Тоді згідно з інтегральною формулою Коші
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Тоді згідно з інтегральною формулою Коші
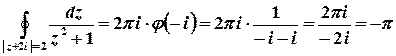 .
.
г) 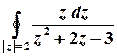 .
.
Розв’язок. Функція 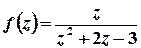 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 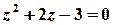 , тобто крім точок
, тобто крім точок 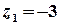 та
та 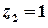 .
.
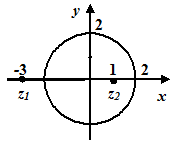 Побудуємо контур інтегрування – лінію
Побудуємо контур інтегрування – лінію 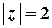 . Це коло з центром у початку координат та радіусом
. Це коло з центром у початку координат та радіусом 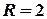 . Точка
. Точка 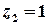 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 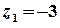 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 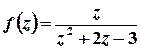 можна записати у вигляді
можна записати у вигляді 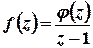 , де
, де 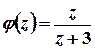 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Згідно з інтегральною формулою Коші
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Згідно з інтегральною формулою Коші
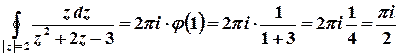 .
.
д) 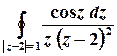
Розв’язок. Функція 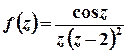 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 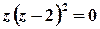 , тобто крім точок
, тобто крім точок 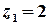 та
та 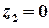 .
.
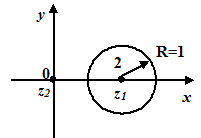
Побудуємо контур інтегрування – лінію 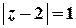 . Це коло з центром у точці
. Це коло з центром у точці 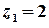 та радіусом
та радіусом 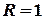 . Точка
. Точка 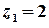 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 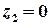 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 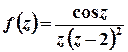 можна записати у вигляді
можна записати у вигляді 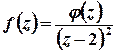 , де
, де 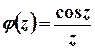 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування.
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування.
Для обчислення інтеграла від цієї функції можна застосувати інтегральну формулу типу Коші
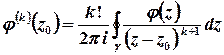 .
.
Для 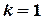 отримаємо
отримаємо 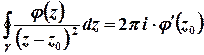 .
.
Тоді 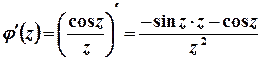 ,
, 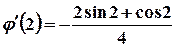 , та
, та
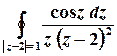
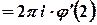
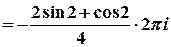
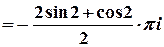 .
.
Приклад 8. Знайти круг збіжності степеневого ряду та побудувати його на комплексній площині. Якщо є можливість, дослідити поведінку ряду на межі кругу.
а) 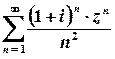
Розв’язок. 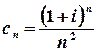 ;
; 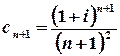 .
.
Обчислимо радіус збіжності :
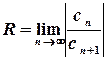
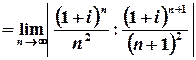
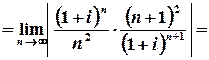
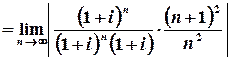
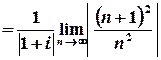
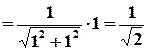 .
.
Ряд абсолютно збігається для всіх 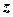 , які задовольняють умові
, які задовольняють умові 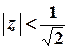 .
. 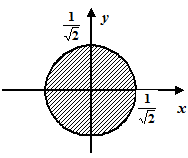 З’ясуємо поведінку ряду у точках, для яких
З’ясуємо поведінку ряду у точках, для яких 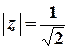 :
:
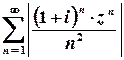
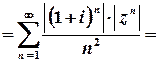
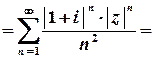
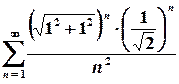
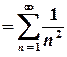 .
.
Цей ряд абсолютно збігається, отже, степеневий ряд є абсолютно збіжним для всіх чисел, для яких 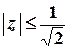 . Цій умові відповідає круг з центром у початку координат та радіусом
. Цій умові відповідає круг з центром у початку координат та радіусом 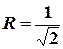 . Граничні точки також входять до області збіжності ряду.
. Граничні точки також входять до області збіжності ряду.
б) 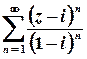 .
.
Розв’язок. 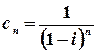 .
.
Обчислимо радіус збіжності :
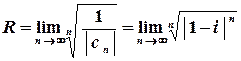
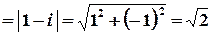 .
.
Таким чином, ряд абсолютно збігається для всіх 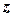 , які задовольняють умові
, які задовольняють умові 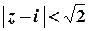 , тобто у внутрішніх точках кругу з центром у точці
, тобто у внутрішніх точках кругу з центром у точці 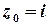 та радіусом
та радіусом 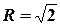 .
.
 Дослідимо поведінку ряду на межі цього кругу, тобто при
Дослідимо поведінку ряду на межі цього кругу, тобто при 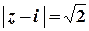 :
:
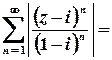
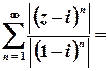
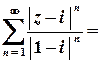
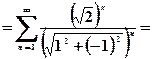
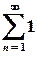 .
.
Цей ряд згідно з необхідною умовою збіжності розбігається ( 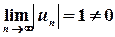 ), отже, на колі
), отже, на колі 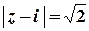 степеневий ряд є розбіжним.
степеневий ряд є розбіжним.
в) 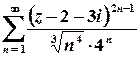
Розв’язок. Це ряд з пропуском степенів, отже, для його дослідження доцільно скористатися ознакою Даламбера або Коші.
Оберемо ознаку Даламбера:
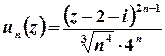 ;
; 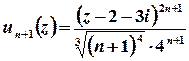 ;
;
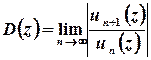
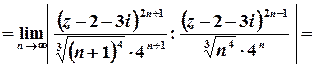
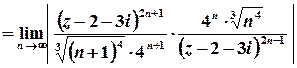
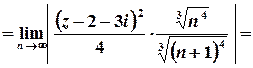
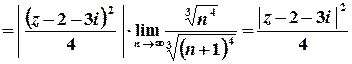 .
.
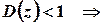
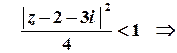
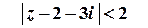 .
.
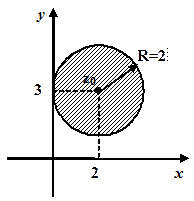 Таким чином, ряд абсолютно збігається для всіх
Таким чином, ряд абсолютно збігається для всіх 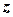 , які задовольняють умові
, які задовольняють умові 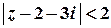 , тобто у внутрішніх точках кругу з центром у точці
, тобто у внутрішніх точках кругу з центром у точці 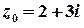 та радіусом
та радіусом 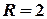 .
.
Дослідимо поведінку ряду на межі цього кругу, тобто для 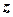 , які задовольняють умові
, які задовольняють умові 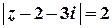 :
:
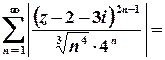
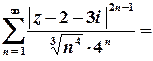
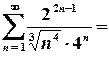
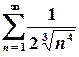 .
.
Цей числовий ряд з додатними членами збігається, отже, степеневий ряд на колі 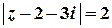 є абсолютно збіжним.
є абсолютно збіжним.
Приклад 9. Знайти лишки функції у всіх її скінченних особливих точках.
а) 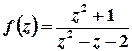 .
.
Розв’язок. Особливі точки функції відповідають умові
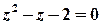 ;
; 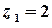 ,
, 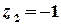 – полюси 1-го порядку.
– полюси 1-го порядку.
Лишки у полюсах 1-го порядку обчислюються за формулою
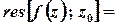
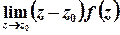 ,
,
тобто 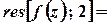
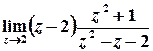
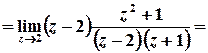
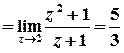 ;
;
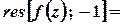
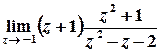
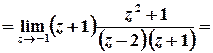
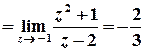 .
.
б) 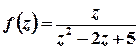 .
.
Розв’язок. 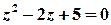 ;
; 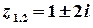 – полюси 1-го порядку.
– полюси 1-го порядку.
Лишки у таких точках можна також обчислити за формулою
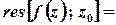
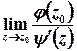 ,
,
де 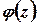 – аналітична функція,
– аналітична функція, 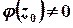 .
.
Тоді 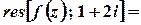
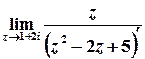
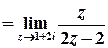
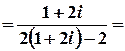
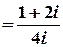
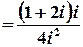
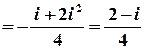 ;
;
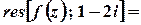
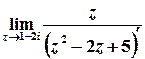
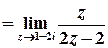
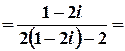
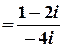
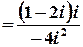
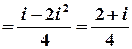 .
.
в) 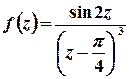 .
.
Розв’язок. 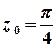 – полюс 3-го порядку.
– полюс 3-го порядку.
Лишок у цій точці обчислюється за формулою
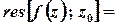
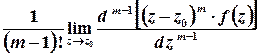 , або для
, або для 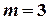
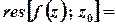
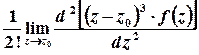 .
.
Тоді 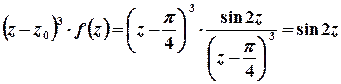 ;
;
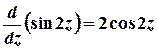 ;
; 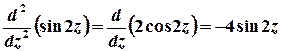 ,
,
отже, 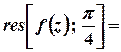
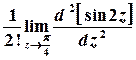
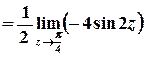
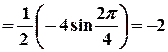 .
.
б) 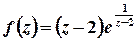 .
.
Розв’язок. Особлива точка 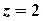 . Для обчислення лишка у цій точці побудуємо розвинення функції у відповідний ряд Лорана. Для цього скористаємося відомим розвиненням показникової функції у степеневий ряд
. Для обчислення лишка у цій точці побудуємо розвинення функції у відповідний ряд Лорана. Для цього скористаємося відомим розвиненням показникової функції у степеневий ряд
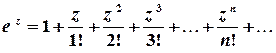 .
.
Тоді 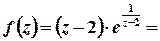
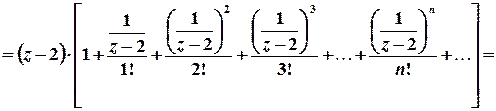
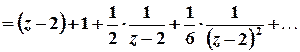 .
.
Згідно з означенням лишка, 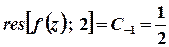 .
.
Тема 2 . Інтегральні перетворення
Література : [2], гл. 8; [3], гл. VI; [4], гл. XIX; [6], гл. 13.
При розгляді цієї теми студент повинен навчитися будувати зображення Лапласа функцій з використанням властивостей перетворення Лапласа та таблиці зображень, оволодіти найпростішими методами відновлення оригіналу за відомим зображенням та навчитися розв’язувати диференціальні рівняння методами операційного числення.
Розглянемо деякі приклади.
Приклад 1. Знайти зображення Лапласа заданих функцій.
а) 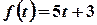 .
.
Розв’язок. Розглядувана функція є лінійною комбінацією функцій, зображення яких відомі:
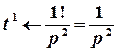 ;
; 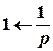 .
.
Тоді
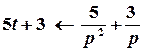 .
.
б) 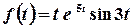 .
.
Розв’язок.
1 спосіб. Зображення Лапласа функції 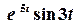 відомо:
відомо:
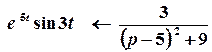 .
.
За теоремою про диференціювання зображення 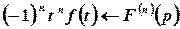
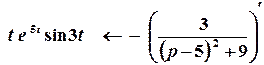 ;
;
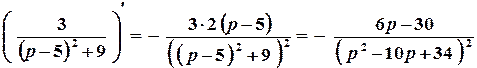 .
.
Остаточно 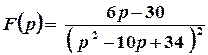 .
.
2 спосіб. Зображення Лапласа функції 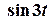 відомо:
відомо:
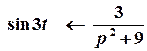 .
.
Скористаємося теоремою про диференціювання зображення:
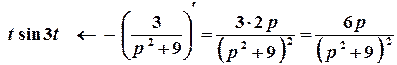 .
.
За теоремою зміщення 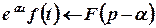 отримаємо:
отримаємо:
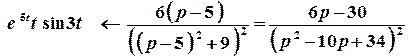 .
.
в) 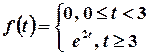 .
.
Розв’язок. Запишемо розглядувану функцію за допомогою функції Хевісайда:
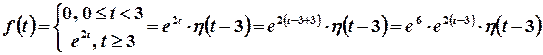 .
.
Зображення функції 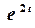 відомо:
відомо:
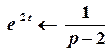 .
.
Згідно з теоремою спізнення 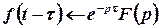 маємо:
маємо:
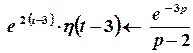 .
.
Остаточно 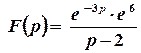 .
.
Приклад 2. Знайти оригінал за заданим зображенням.
а) 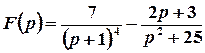 .
.
Розв’язок. Розглядувану функцію дуже легко записати як лінійну комбінацію табличних:
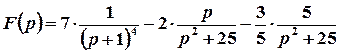 ;
;
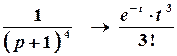 ;
; 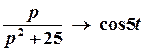 ;
; 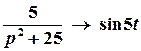 .
.
Тоді 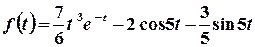 .
.
б) 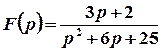 .
.
Розв’язок.
1 спосіб. Запишемо задане зображення у вигляді, який дозволяє використати таблицю оригіналів.
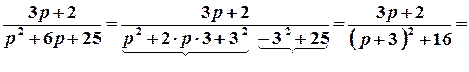
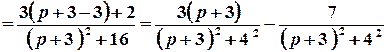 .
.
Отже, 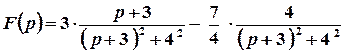 .
.
Тоді шуканим оригіналом є функція 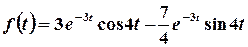 .
.
2 спосіб. Функція 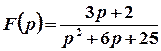 є правильним дробом. Особливі точки цієї функції задаються умовою
є правильним дробом. Особливі точки цієї функції задаються умовою 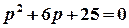 . Цій рівності відповідають числа
. Цій рівності відповідають числа 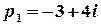 та
та 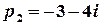 , які є комплексно спряженими полюсами 1-го порядку.
, які є комплексно спряженими полюсами 1-го порядку.
Тоді шуканий оригінал можна знайти за допомогою лишків:
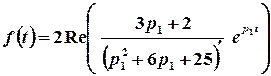
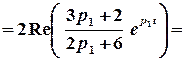
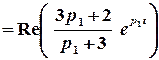 ;
;
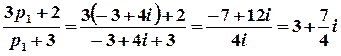 ;
;
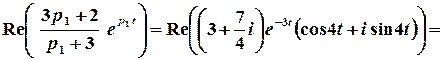
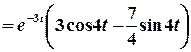 .
.
Таким чином, 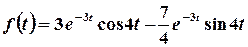 .
.
в) 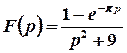 .
.
Розв’язок. Запишемо функцію у вигляді, якій дозволяє скористатися таблицею оригіналів та властивостями перетворення Лапласа.
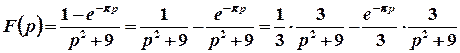 .
.
Перший доданок є табличним, оригінал другого доданку можна знайти за допомогою теореми спізнення:
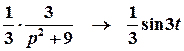 ;
; 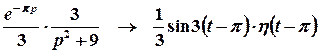 .
.
Тоді 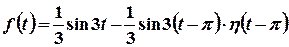 . Це означає, що для
. Це означає, що для 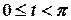
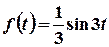 , а для
, а для 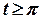
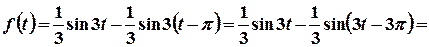
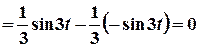 .
.
Остаточно 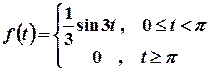 .
.
Приклад 3. Розв’язати за допомогою операційного метода задачу Коші
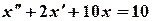 ,
, 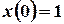 ,
, 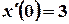 .
.
Розв’язок. Застосуємо до диференціального рівняння перетворення Лапласа. Позначимо як 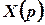 зображення шуканої функції
зображення шуканої функції 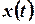 :
:
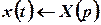 .
.
Тоді зображення похідних цієї функції можна побудувати за теоремою про диференціювання оригіналу:
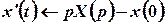 ,
, 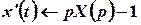 ;
;
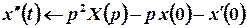 ,
, 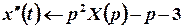 .
.
Зображення правої частини диференціального рівняння будується за допомогою таблиці зображень найпростіших функцій:
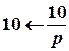 .
.
Тоді функція 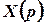 буде розв’язком операторного рівняння
буде розв’язком операторного рівняння
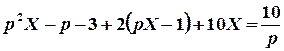 .
.
Розв’яжемо це рівняння.
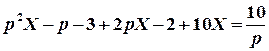 ;
;
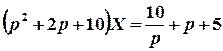 ;
;
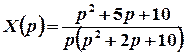 .
.
Знайдемо оригінал, який відповідає отриманому зображенню.
1 спосіб. Запишемо зображення 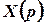 у вигляді суми функцій, оригінали для яких відомі:
у вигляді суми функцій, оригінали для яких відомі:
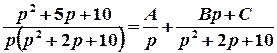 ;
;
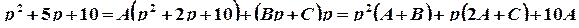 ;
;
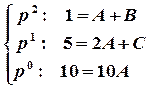 ;
; 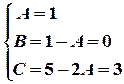 ;
;
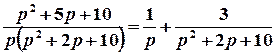 ;
; 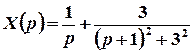 .
.
Тоді шуканий розв’язок задачі Коші дорівнює
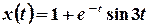 .
.
2 спосіб. Отримане зображення 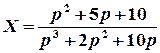 є правильним алгебраїчним дробом, отже, шуканий оригінал можна знайти за допомогою лишків:
є правильним алгебраїчним дробом, отже, шуканий оригінал можна знайти за допомогою лишків:
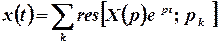 .
.
Особливі точки функції 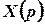 –
– 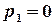 та
та 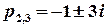 – є полюсами 1-го порядку, отже
– є полюсами 1-го порядку, отже
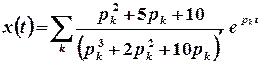 , або
, або 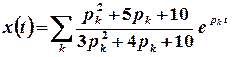 .
.
Полюс 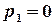 є дійсним, а полюси
є дійсним, а полюси 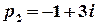 та
та 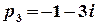 – комплексно спряжені, отже,
– комплексно спряжені, отже,
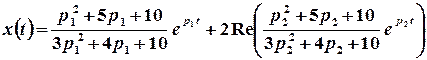 ;
;
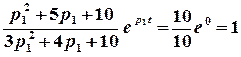 ;
;
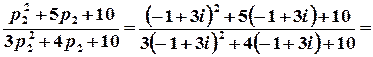
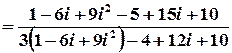
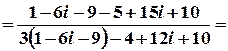
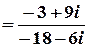
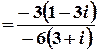
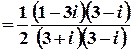
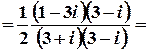
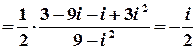 ;
;
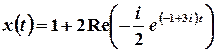
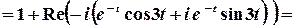
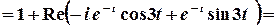
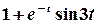 .
.
Остаточно, 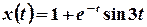 .
.
Дата: 2019-03-05, просмотров: 417.