МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ

РОБОЧА ПРОГРАМА,
Методичні вказівки та індивідуальні завдання
До вивчення дисципліни «Вища математика»
( розділ « Функції комплексної змінної та інтегральні
перетворення») для студентів напряму 6.050202 –
автоматизація та комп’ютерно-інтегровані
Технології
Дніпропетровськ НМетАУ 2010
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНА МЕТАЛУРГІЙНА АКАДЕМІЯ УКРАЇНИ
РОБОЧА ПРОГРАМА,
Методичні вказівки та індивідуальні завдання
До вивчення дисципліни «Вища математика»
( розділ « Функції комплексної змінної та інтегральні
перетворення») для студентів напряму 6.050202 –
автоматизація та комп’ютерно-інтегровані
Технології
ЗАТВЕРДЖЕНО
на засіданні Вченої ради
Академії
Протокол № 10 від 18.12.09
Дніпропетровськ НМетАУ 2010
УДК 517(07)
Робоча програма, методичні вказівки та індивідуальні завдання до вивчення
дисципліни «Вища математика» (розділ «Функції комплексної змінної та інтегральні перетворення») для студентів напряму 6.050202- автоматизація та комп’ютерно-інтегровані технології / Укл.: О.Є. Запорожченко, І.Б. Кочеткова, Л.Ф. Сушко, М.С. Сазонова . – Дніпропетровськ: НМетАУ, 2010. – 40 с.
Наведені рекомендації до вивчення дисципліни «Вища математика» (розділ «Функції комплексної змінної та інтегральні перетворення»); необхідний обсяг знань та умінь студентів у результаті її вивчення;література, що рекомендується; довідковий матеріал; методичні вказівки до вивчення кожної теми; варіанти індивідуальних завдань.
Призначена для студентів напряму 6.050202- автоматизація та комп’ютерно-інтегровані технології заочної
форми навчання.
Укладачі: О.Є. Запорожченко, канд. фіз.-мат. наук, доц.
І.Б. Кочеткова, асист.
Л.Ф. Сушко, асист.
М.С. Сазонова, канд. фіз.-мат. наук, доц.
Відповідальний за випуск А.В. Павленко, д-р фіз.-мат. наук, проф.
Рецензент Г.Г. Швачич, канд. техн. наук, проф.(НМетАУ)
ЗАГАЛЬНІ РЕКОМЕНДАЦІЇ СТУДЕНТАМ ЗАОЧНОЇ
Програма дисципліни «Вища математика»
(4 семестр)
ТЕОРІЯ ФУНКЦІЙ КОМПЛЕКСНОЇ ЗМІННОЇ
1. Комплексні числа та дії над ними.
2. Функції комплексної змінної. Границя та неперервність функцій комплексної змінної. Елементарні функції.
3. Диференційовність функції комплексної змінної. Умови Коші-Рімана. Аналітичні функції.
4. Інтегрування комплексних функцій. Теорема Коші. Інтегральна формула Коші.
5. Ряди з комплексними членами. Степеневі ряди. Круг збіжності.
6. Розвинення функцій в ряд Лорана. Ізольовані особливі точки. Лишки та їх застосування.
ІНТЕГРАЛЬНІ ПЕРЕТВОРЕННЯ
1. Знаходження зображень функцій. Зображення похідних.
2. Розшукування оригінала за зображенням.
3. Застосування операційного числення до розв’язування диференціальних рівнянь.
СПИСОК ЛІТЕРАТУРИ
1. Привалов И.И. Введение в теорию функций комплексного переменного. – М.: Наука, 1977. – 444 с.
2. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. – М.: Наука, 1974. – 320 с.
3. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688 с.
4.Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2. – М.: Наука, 1985. – 560 с.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. – М.: Наука, 2000. – 416 с.
6. Сборник задач по математике для втузов. Специальные разделы математического анализа / Под ред. А.В.Ефимова, Б.П. Демидовича. – М.: Наука, 1985. – 368 с.
7. Е.С. Синайский, Л.В. Новикова, Л.И. Заславская. Высшая математика: Навч. посібник. – Дніпропетровськ: Національний гірничий університет, 2006. –
Ч.ІІ. – 452 с.
8. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984. – 832 с.
9. Справочник по специальным функциям. – М. : Наука, 1979. – 832 с.
ДОВІДКОВИЙ МАТЕРІАЛ
Функції комплексної змінної
Якщо задано закон 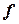 , згідно з яким кожному значенню
, згідно з яким кожному значенню 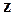 , яке належить множині
, яке належить множині 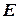 , відповідає певне значення
, відповідає певне значення 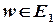 , то кажуть, що задана однозначна функція
, то кажуть, що задана однозначна функція 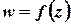 , яка визначена на
, яка визначена на 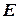 та набуває значень в
та набуває значень в 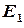 . Якщо значенню
. Якщо значенню 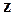 відповідає декілька значень
відповідає декілька значень 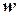 , то функція є багатозначною.
, то функція є багатозначною.
Функцію комплексної змінної можна записати у вигляді
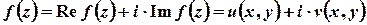 ,
,
де 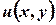 та
та 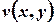 – функції дійсних змінних
– функції дійсних змінних 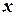 та
та 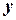 .
.
Існування границі функції комплексної змінної 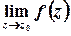 еквівалентне одночасному існуванню границь дійсної та уявної частин
еквівалентне одночасному існуванню границь дійсної та уявної частин 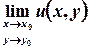 та
та 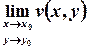 . Аналогічно неперервність функції
. Аналогічно неперервність функції 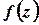 у точці
у точці 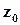 еквівалентна неперервності функцій
еквівалентна неперервності функцій 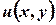 та
та 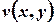 у точці
у точці 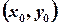 .
.
Функція, неперервна у кожній точці області 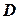 , називається неперервною у цій області.
, називається неперервною у цій області.
Елементарні функції комплексної змінної. Введемо показникову функцію комплексної змінної 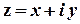 за правилом
за правилом
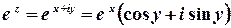 .
.
Тригонометричні та гіперболічні функції зв’язані з показниковою співвідношеннями
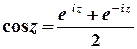 ;
; 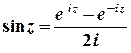 ;
; 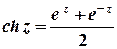 ;
; 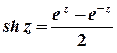 ;
;
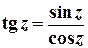
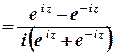 . ;
. ; 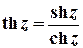
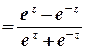 .
.
Функції, які введені за цими формулами, по-перше, для дійсних значень аргумента 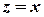 співпадають з відповідними функціями дійсної змінної, та, по-друге, зберігають всі властивості функцій дійсної змінної.
співпадають з відповідними функціями дійсної змінної, та, по-друге, зберігають всі властивості функцій дійсної змінної.
Також є очевидними властивості
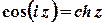 ;
; 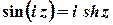 ;
; 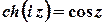 ;
; 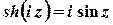 .
.
Функції 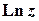 ,
, 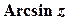 ,
, 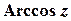 ,
, 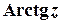 визначають як обернені до функцій
визначають як обернені до функцій 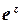 ,
, 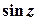 ,
, 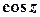 ,
, 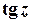 відповідно. Зокрема,
відповідно. Зокрема,
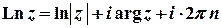 ,
, 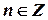 ,
,
а головне значення логарифмічної функції визначається як
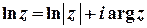 (величина
(величина 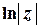 є функцією дійсного аргументу).
є функцією дійсного аргументу).
Особливі точки. Лишки
Функція 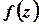 , аналітична у внутрішніх точках круга
, аналітична у внутрішніх точках круга 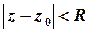 , може бути представлена у цьому крузі збіжним степеневим рядом
, може бути представлена у цьому крузі збіжним степеневим рядом 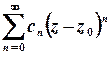 , який називається рядом Тейлора.
, який називається рядом Тейлора.
Для елементарних функцій комплексної змінної зберігаються розвинення у ряди Тейлора та Маклорена, отримані для функцій дійсної змінної:
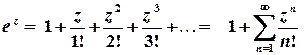 ,
, 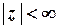 ;
;
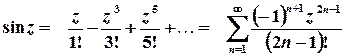 ,
, 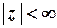 ;
;
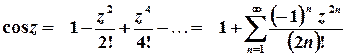 ,
, 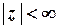 ;
;
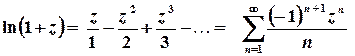 ,
, 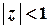 ;
;
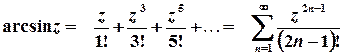 ,
, 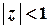 ;
;
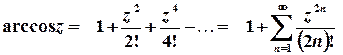 ,
, 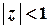 тощо.
тощо.
Якщо функція 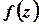 є аналітичною у кільці
є аналітичною у кільці 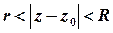 , то вона може бути представлена у точках цього кільця своїм рядом Лорана
, то вона може бути представлена у точках цього кільця своїм рядом Лорана
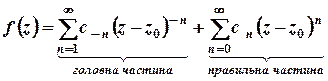 ,
,
де 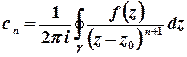 ,
, 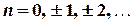 , інтегрування виконується вздовж кола
, інтегрування виконується вздовж кола 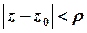 ,
, 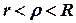 .
.
Радіуси 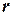 та
та 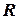 зв’язані з коефіцієнтами Лорана співвідношеннями
зв’язані з коефіцієнтами Лорана співвідношеннями
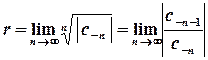 та
та 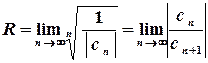 .
.
Точка 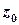 називається ізольованою особливою точкою функції
називається ізольованою особливою точкою функції 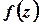 , якщо
, якщо 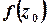 не визначена, та існує окіл
не визначена, та існує окіл 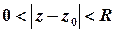 , в якому функція
, в якому функція 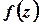 є аналітичною. Особлива точка
є аналітичною. Особлива точка 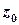 називається
називається
– усувною, якщо існує скінчений 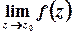 ;
;
– полюсом, якщо 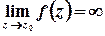 ;
;
– істотно особливою точкою, якщо 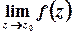 не існує.
не існує.
Число 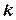 називається порядком нуля функції
називається порядком нуля функції 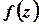 в точці
в точці 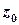 , якщо функція
, якщо функція 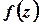 аналітична в точці
аналітична в точці 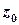 ,
, 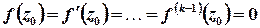 , та
, та 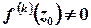 . Якщо точка
. Якщо точка 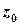 є нулем порядку
є нулем порядку 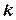 для функції
для функції 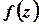 , то вона є полюсом порядку
, то вона є полюсом порядку 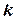 для функції
для функції 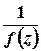 . Зокрема, число
. Зокрема, число 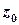 є полюсом порядку
є полюсом порядку 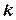 для функції
для функції 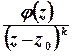 , якщо
, якщо 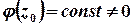 .
.
Якщо особлива точка 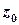 є усувною, всі коефіцієнти головної частини відповідного ряду Лорана дорівнюють нулю, у випадку полюса порядку
є усувною, всі коефіцієнти головної частини відповідного ряду Лорана дорівнюють нулю, у випадку полюса порядку 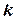 мають місце умови
мають місце умови 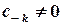 ,
, 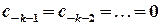 , нарешті, для істотно особливої точки існує нескінченна множина відмінних від нуля коефіцієнтів головної частини ряду Лорана.
, нарешті, для істотно особливої точки існує нескінченна множина відмінних від нуля коефіцієнтів головної частини ряду Лорана.
Лишком функції 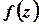 відносно скінченої точки
відносно скінченої точки 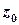 називається величина
називається величина
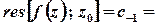
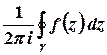 ,
,
де 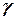 – будь-яке додатно орієнтоване коло
– будь-яке додатно орієнтоване коло 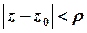 , яке лежить в кільці збіжності ряду Лорана.
, яке лежить в кільці збіжності ряду Лорана.
Якщо точка 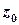 є точкою аналітичності функції
є точкою аналітичності функції 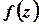 або її усувною особливою точкою, то
або її усувною особливою точкою, то 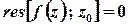 .
.
Лишок в простому полюсі обчислюють за формулами
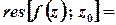
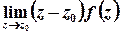 або
або
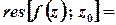
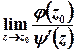 , де
, де 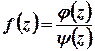 , причому
, причому 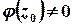 .
.
Якщо 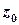 – кратний полюс порядку
– кратний полюс порядку 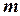 , то
, то
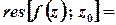
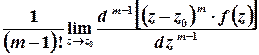 .
.
Для обчислення лишків в істотно особливих точках знаходять коефіцієнт 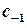 ряду Лорана інтегруванням або за допомогою відомих розвинень функцій у степеневі ряди.
ряду Лорана інтегруванням або за допомогою відомих розвинень функцій у степеневі ряди.
Основна теорема про лишки. Якщо функція 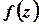 є аналітичною у замкненій області
є аналітичною у замкненій області 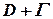 за винятком скінченої кількості особливих точок
за винятком скінченої кількості особливих точок 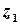 ,
, 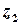 ,…
,… 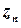 , які лежать усередині
, які лежать усередині 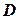 , то
, то
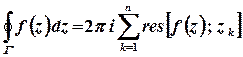 .
.
Операційне числення
Операційний метод – це специфічний спосіб розв’язування різних математичних задач, в першу чергу, диференційних рівнянь. Він базується на застосуванні інтегральних перетворень, зокрема, перетворення Лапласа, та складається з таких етапів:
1) від шуканої функції 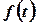 переходять до функції
переходять до функції 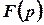 комплексної змінної, яку називають зображенням шуканої функції;
комплексної змінної, яку називають зображенням шуканої функції;
2) над зображенням виконують операції, які відповідають заданим операціям над шуканою функцією, – отримують так зване операторне рівняння для зображення 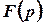 ;
;
3) операторне рівняння розв’язують відносно 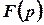 ;
;
4) від отриманого зображення 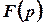 переходять до оригіналу, який є шуканою функцією.
переходять до оригіналу, який є шуканою функцією.
КОНТРОЛЬНА РОБОТА № 7
Тема 1. Теорія функцій комплексної змінної
Література : [1], гл. I-VII; [2], гл. 1, § 1-6, гл. 2, гл. 4,гл. 5, § 1; [3], гл. I;
[6], гл. 11, § 1, 2, 4, гл. 12, § 1, 3, 5, 6.
При вивченні матеріалу цієї теми студент повинен усвідомити основні поняття теорії функції комплексної змінної , навчитися обчислювати значення елементарних функцій, інтегралів вздовж замкненого контуру, будувати розвинення функцій в ряд Лорана та обчислювати лишки.
Розглянемо приклади.
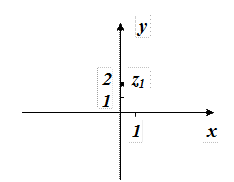
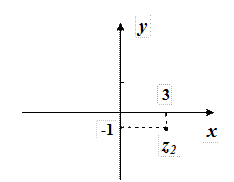
Приклад 1. Побудувати на комплексній площині числа 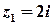 ,
, 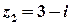 .
.
Розв’язок. Числу 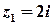 на координатній площині відповідає точка з координатами
на координатній площині відповідає точка з координатами 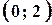 , а числу
, а числу 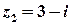 – точка
– точка 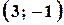 .
.
Приклад 2. Виконати арифметичні дії з комплексними числами 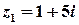 ,
, 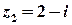 .
.
Розв’язок. 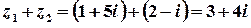 ;
;
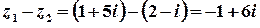 ;
;
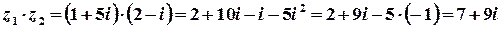 ;
;
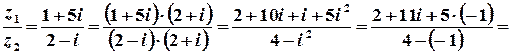
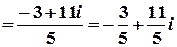 .
.
Приклад 3. Записати комплексні числа у показниковій та тригонометричній формах.
а) 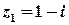 .
.
Розв’язок. Обчислимо модуль та головне значення аргумента комплексного числа.
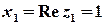 ,
, 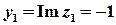 .
.
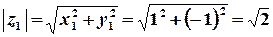 ;
;
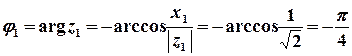 , або
, або
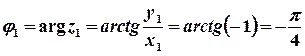 .
.
Тоді 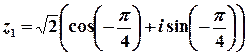 – тригонометрична форма,
– тригонометрична форма,
та 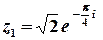 – показникова форма.
– показникова форма.
б) 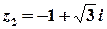 .
.
Розв’язок. 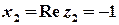 ,
, 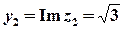 ;
;
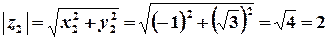 ;
;
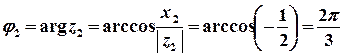 , або
, або
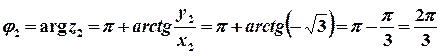 .
.
Тоді 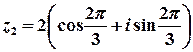 – тригонометрична форма,
– тригонометрична форма,
та 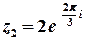 – показникова форма.
– показникова форма.
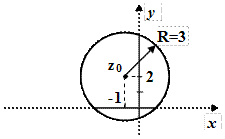
Приклад 4. Зобразити геометричне місце точок, які задовольняють умові
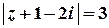 .
.
Розв’язок.
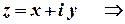
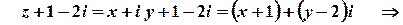
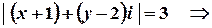
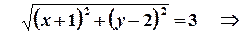
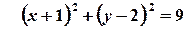 .
.
Це рівняння кола з центром у точці 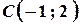 , яка відповідає комплексному числу
, яка відповідає комплексному числу 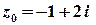 . Радіус кола дорівнює
. Радіус кола дорівнює 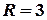 .
.
Приклад 5. Обчислити значення функцій комплексної змінної.
а) 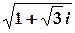 .
.
Розв’язок. Обчислимо модуль та головне значення аргументу комплексного числа.
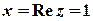 ,
, 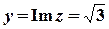 ;
; 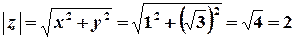 ;
;
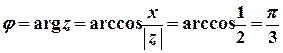 .
.
Тоді 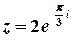 . За правилом обчислення кореня з комплексного числа маємо
. За правилом обчислення кореня з комплексного числа маємо
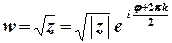 ,
, 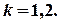
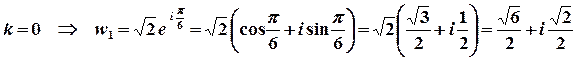
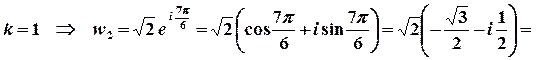
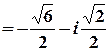 .
.
б) 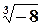 .
.
Розв’язок. 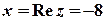 ,
, 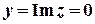 ;
; 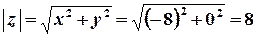 ;
;
 .
.
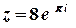 .
.
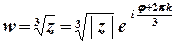 ,
, 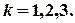
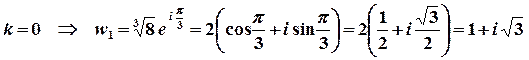
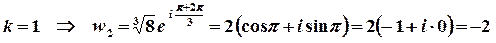
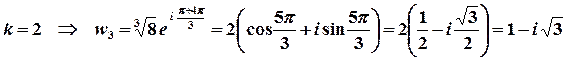 .
.
в) 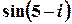 .
.
Розв’язок.
1 спосіб. Значення синуса комплексного аргумента можна обчислити з використанням зв’язку цієї тригонометричної та показникової функції.
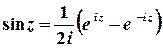 ;
;
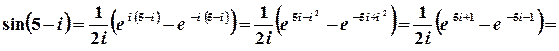
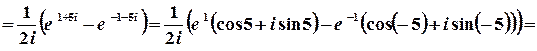
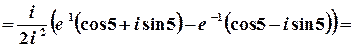
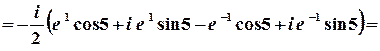
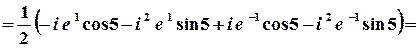
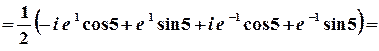
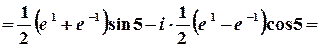
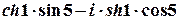 .
.
2 спосіб. Для тригонометричних функцій комплексної змінної є вірними всі властивості функцій дійсної змінної.
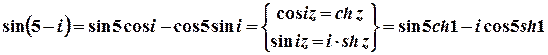 .
.
г) 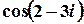 .
.
Розв’язок.
1 спосіб. 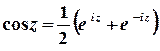
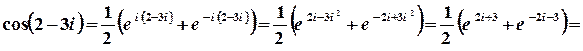
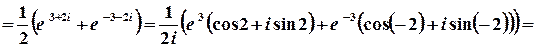
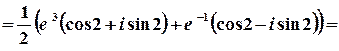
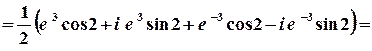
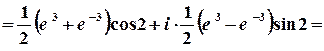
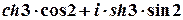 .
.
2 спосіб.
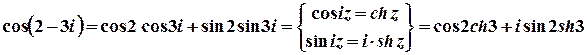 .
.
д) 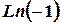 .
.
Розв’язок. 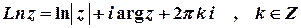 .
.
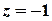 ,
, 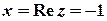 ,
, 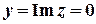 ,
, 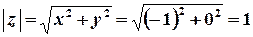 ;
;
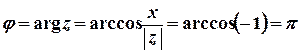 ;
;
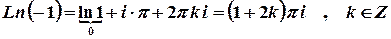 .
.
е) 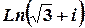 .
.
Розв’язок. 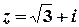 ,
, 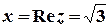 ,
, 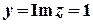 ,
, 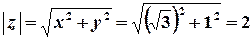 ;
; 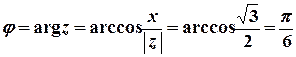 ;
;
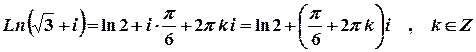 .
.
Приклад 6. З’ясувати, чи є функція 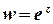 аналітичною.
аналітичною.
Розв’язок. 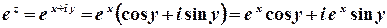 .
.
Отже, 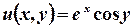 ;
; 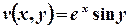 .
.
Обчислимо частинні похідні цих функцій.
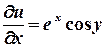 ;
; 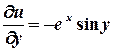 ;
;
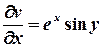 ;
; 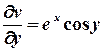 .
.
Умови Коші – Рімана 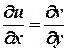 ,
, 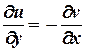 виконуються для будь-яких дійсних х та у , отже, функція
виконуються для будь-яких дійсних х та у , отже, функція 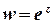 є аналітичною на всій комплексній площині.
є аналітичною на всій комплексній площині.
Приклад 7. Обчислити інтеграли по замкнутому контуру.
а) 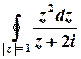 .
.
Розв’язок. Функція 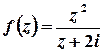 аналітична на всій комплексній площині, крім точки
аналітична на всій комплексній площині, крім точки 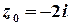 .
.
Побудуємо контур інтегрування – коло 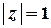 .
.
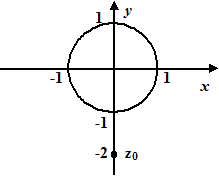 Точка
Точка 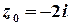 розташована поза колом
розташована поза колом 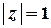 , тому
, тому 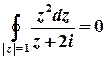
б) 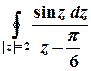 .
.
Розв’язок. Функція 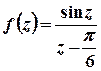 аналітична на всій комплексній площині, крім точки
аналітична на всій комплексній площині, крім точки 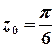 .
.
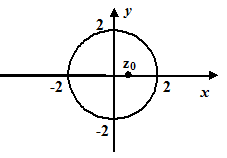 Побудуємо контур інтегрування – коло
Побудуємо контур інтегрування – коло 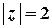 . Точка
. Точка 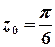 – внутрішня точка цього кола, функція
– внутрішня точка цього кола, функція 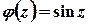 аналітична, тому за інтегральною формулою Коші
аналітична, тому за інтегральною формулою Коші
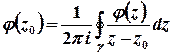
(або 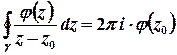 ) отримаємо
) отримаємо
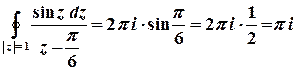 .
.
в) 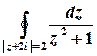 .
.
Розв’язок. Функція 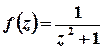 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 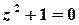 , тобто крім точок
, тобто крім точок 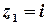 та
та 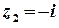 .
.
Побудуємо контур інтегрування – лінію 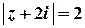 . Це коло з центром в точці
. Це коло з центром в точці 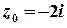 та радіусом
та радіусом 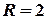 .
.
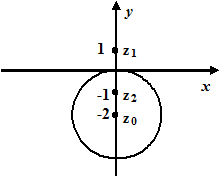 Точка
Точка 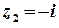 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 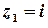 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 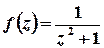 можна записати у вигляді
можна записати у вигляді 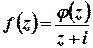 , де
, де 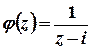 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Тоді згідно з інтегральною формулою Коші
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Тоді згідно з інтегральною формулою Коші
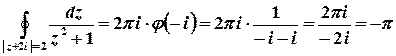 .
.
г) 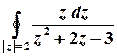 .
.
Розв’язок. Функція 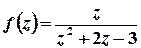 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 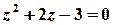 , тобто крім точок
, тобто крім точок 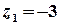 та
та 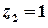 .
.
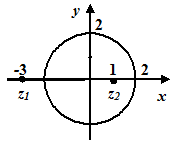 Побудуємо контур інтегрування – лінію
Побудуємо контур інтегрування – лінію 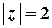 . Це коло з центром у початку координат та радіусом
. Це коло з центром у початку координат та радіусом 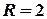 . Точка
. Точка 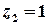 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 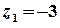 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 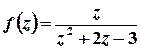 можна записати у вигляді
можна записати у вигляді 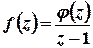 , де
, де 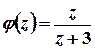 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Згідно з інтегральною формулою Коші
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування. Згідно з інтегральною формулою Коші
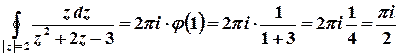 .
.
д) 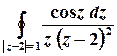
Розв’язок. Функція 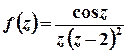 аналітична на всій комплексній площині, крім точок, в яких справджується рівність
аналітична на всій комплексній площині, крім точок, в яких справджується рівність 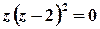 , тобто крім точок
, тобто крім точок 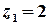 та
та 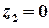 .
.
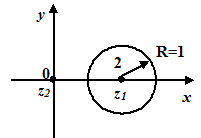
Побудуємо контур інтегрування – лінію 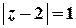 . Це коло з центром у точці
. Це коло з центром у точці 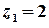 та радіусом
та радіусом 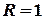 . Точка
. Точка 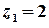 – внутрішня точка цього кола, точка
– внутрішня точка цього кола, точка 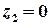 лежить поза колом. Тоді підінтегральну функцію
лежить поза колом. Тоді підінтегральну функцію 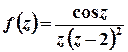 можна записати у вигляді
можна записати у вигляді 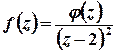 , де
, де 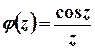 – функція, аналітична у всіх точках області, обмеженої контуром інтегрування.
– функція, аналітична у всіх точках області, обмеженої контуром інтегрування.
Для обчислення інтеграла від цієї функції можна застосувати інтегральну формулу типу Коші
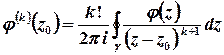 .
.
Для 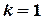 отримаємо
отримаємо 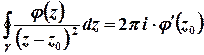 .
.
Тоді 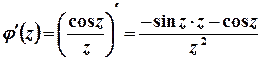 ,
, 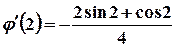 , та
, та
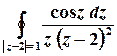
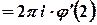
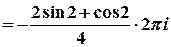
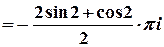 .
.
Приклад 8. Знайти круг збіжності степеневого ряду та побудувати його на комплексній площині. Якщо є можливість, дослідити поведінку ряду на межі кругу.
а) 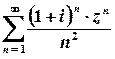
Розв’язок. 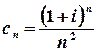 ;
; 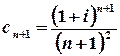 .
.
Обчислимо радіус збіжності :
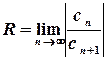
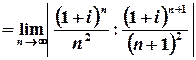
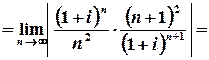
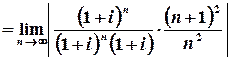
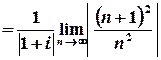
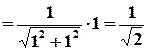 .
.
Ряд абсолютно збігається для всіх 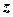 , які задовольняють умові
, які задовольняють умові 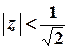 .
. 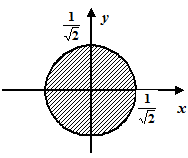 З’ясуємо поведінку ряду у точках, для яких
З’ясуємо поведінку ряду у точках, для яких 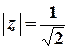 :
:
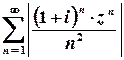
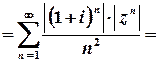
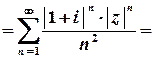
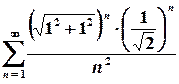
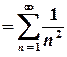 .
.
Цей ряд абсолютно збігається, отже, степеневий ряд є абсолютно збіжним для всіх чисел, для яких 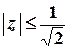 . Цій умові відповідає круг з центром у початку координат та радіусом
. Цій умові відповідає круг з центром у початку координат та радіусом 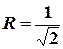 . Граничні точки також входять до області збіжності ряду.
. Граничні точки також входять до області збіжності ряду.
б) 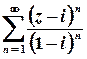 .
.
Розв’язок. 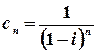 .
.
Обчислимо радіус збіжності :
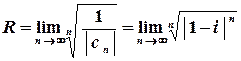
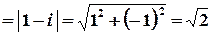 .
.
Таким чином, ряд абсолютно збігається для всіх 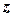 , які задовольняють умові
, які задовольняють умові 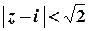 , тобто у внутрішніх точках кругу з центром у точці
, тобто у внутрішніх точках кругу з центром у точці 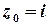 та радіусом
та радіусом 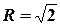 .
.
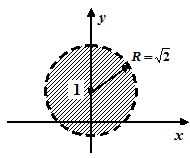 Дослідимо поведінку ряду на межі цього кругу, тобто при
Дослідимо поведінку ряду на межі цього кругу, тобто при 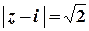 :
:
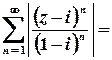
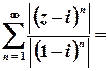
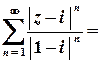
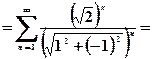
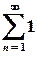 .
.
Цей ряд згідно з необхідною умовою збіжності розбігається ( 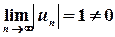 ), отже, на колі
), отже, на колі 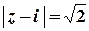 степеневий ряд є розбіжним.
степеневий ряд є розбіжним.
в) 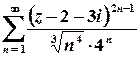
Розв’язок. Це ряд з пропуском степенів, отже, для його дослідження доцільно скористатися ознакою Даламбера або Коші.
Оберемо ознаку Даламбера:
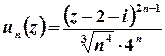 ;
; 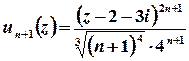 ;
;
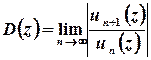
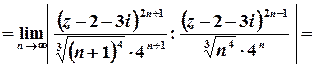
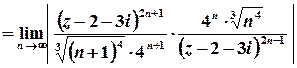
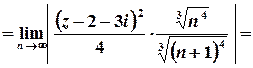
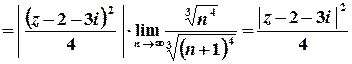 .
.
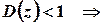
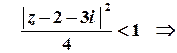
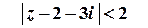 .
.
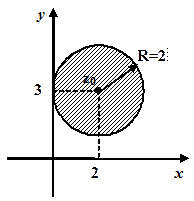 Таким чином, ряд абсолютно збігається для всіх
Таким чином, ряд абсолютно збігається для всіх 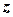 , які задовольняють умові
, які задовольняють умові 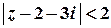 , тобто у внутрішніх точках кругу з центром у точці
, тобто у внутрішніх точках кругу з центром у точці 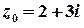 та радіусом
та радіусом 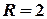 .
.
Дослідимо поведінку ряду на межі цього кругу, тобто для 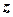 , які задовольняють умові
, які задовольняють умові 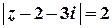 :
:
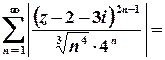
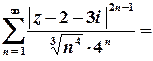
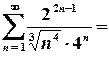
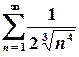 .
.
Цей числовий ряд з додатними членами збігається, отже, степеневий ряд на колі 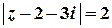 є абсолютно збіжним.
є абсолютно збіжним.
Приклад 9. Знайти лишки функції у всіх її скінченних особливих точках.
а) 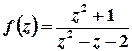 .
.
Розв’язок. Особливі точки функції відповідають умові
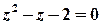 ;
; 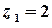 ,
, 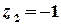 – полюси 1-го порядку.
– полюси 1-го порядку.
Лишки у полюсах 1-го порядку обчислюються за формулою
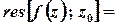
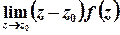 ,
,
тобто 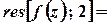
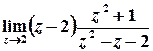
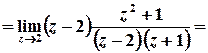
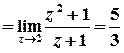 ;
;
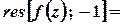
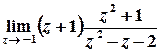
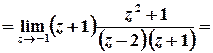
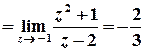 .
.
б) 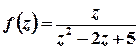 .
.
Розв’язок. 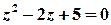 ;
; 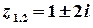 – полюси 1-го порядку.
– полюси 1-го порядку.
Лишки у таких точках можна також обчислити за формулою
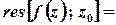
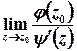 ,
,
де 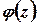 – аналітична функція,
– аналітична функція, 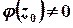 .
.
Тоді 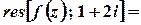
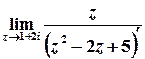
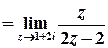
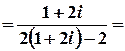
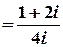
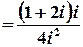
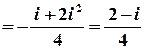 ;
;
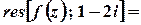
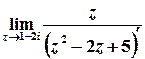
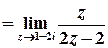
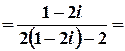
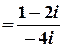
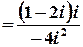
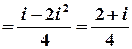 .
.
в) 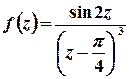 .
.
Розв’язок. 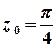 – полюс 3-го порядку.
– полюс 3-го порядку.
Лишок у цій точці обчислюється за формулою
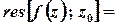
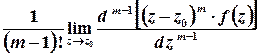 , або для
, або для 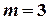
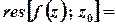
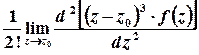 .
.
Тоді 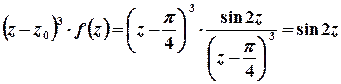 ;
;
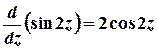 ;
; 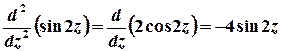 ,
,
отже, 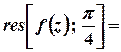
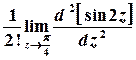
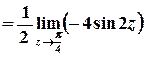
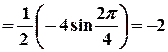 .
.
б) 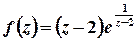 .
.
Розв’язок. Особлива точка 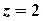 . Для обчислення лишка у цій точці побудуємо розвинення функції у відповідний ряд Лорана. Для цього скористаємося відомим розвиненням показникової функції у степеневий ряд
. Для обчислення лишка у цій точці побудуємо розвинення функції у відповідний ряд Лорана. Для цього скористаємося відомим розвиненням показникової функції у степеневий ряд
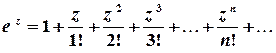 .
.
Тоді 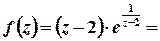
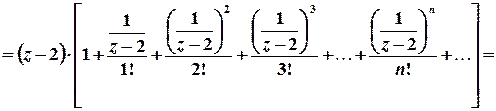
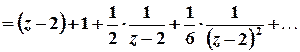 .
.
Згідно з означенням лишка, 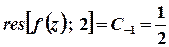 .
.
Тема 2 . Інтегральні перетворення
Література : [2], гл. 8; [3], гл. VI; [4], гл. XIX; [6], гл. 13.
При розгляді цієї теми студент повинен навчитися будувати зображення Лапласа функцій з використанням властивостей перетворення Лапласа та таблиці зображень, оволодіти найпростішими методами відновлення оригіналу за відомим зображенням та навчитися розв’язувати диференціальні рівняння методами операційного числення.
Розглянемо деякі приклади.
Приклад 1. Знайти зображення Лапласа заданих функцій.
а) 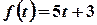 .
.
Розв’язок. Розглядувана функція є лінійною комбінацією функцій, зображення яких відомі:
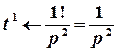 ;
; 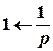 .
.
Тоді
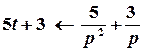 .
.
б) 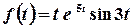 .
.
Розв’язок.
1 спосіб. Зображення Лапласа функції 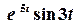 відомо:
відомо:
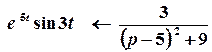 .
.
За теоремою про диференціювання зображення 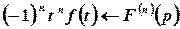
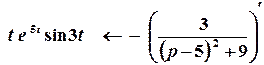 ;
;
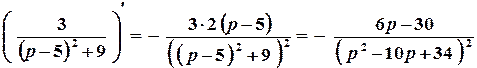 .
.
Остаточно 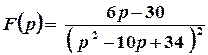 .
.
2 спосіб. Зображення Лапласа функції 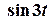 відомо:
відомо:
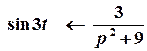 .
.
Скористаємося теоремою про диференціювання зображення:
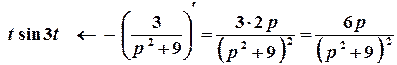 .
.
За теоремою зміщення 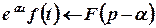 отримаємо:
отримаємо:
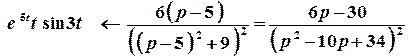 .
.
в) 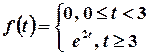 .
.
Розв’язок. Запишемо розглядувану функцію за допомогою функції Хевісайда:
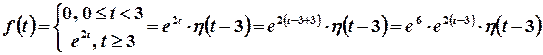 .
.
Зображення функції 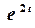 відомо:
відомо:
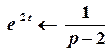 .
.
Згідно з теоремою спізнення 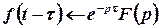 маємо:
маємо:
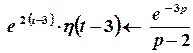 .
.
Остаточно 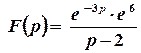 .
.
Приклад 2. Знайти оригінал за заданим зображенням.
а) 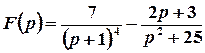 .
.
Розв’язок. Розглядувану функцію дуже легко записати як лінійну комбінацію табличних:
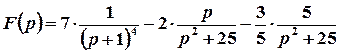 ;
;
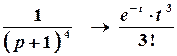 ;
; 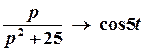 ;
; 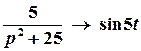 .
.
Тоді 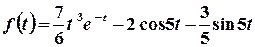 .
.
б) 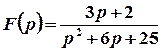 .
.
Розв’язок.
1 спосіб. Запишемо задане зображення у вигляді, який дозволяє використати таблицю оригіналів.
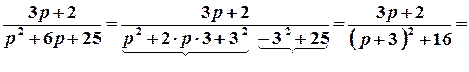
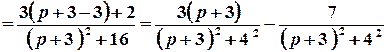 .
.
Отже, 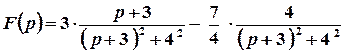 .
.
Тоді шуканим оригіналом є функція 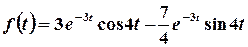 .
.
2 спосіб. Функція 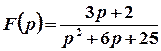 є правильним дробом. Особливі точки цієї функції задаються умовою
є правильним дробом. Особливі точки цієї функції задаються умовою 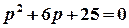 . Цій рівності відповідають числа
. Цій рівності відповідають числа 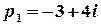 та
та 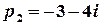 , які є комплексно спряженими полюсами 1-го порядку.
, які є комплексно спряженими полюсами 1-го порядку.
Тоді шуканий оригінал можна знайти за допомогою лишків:
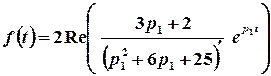
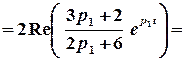
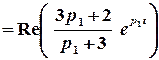 ;
;
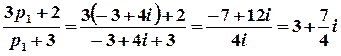 ;
;
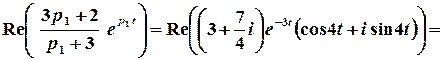
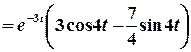 .
.
Таким чином, 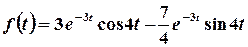 .
.
в) 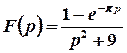 .
.
Розв’язок. Запишемо функцію у вигляді, якій дозволяє скористатися таблицею оригіналів та властивостями перетворення Лапласа.
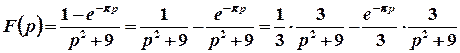 .
.
Перший доданок є табличним, оригінал другого доданку можна знайти за допомогою теореми спізнення:
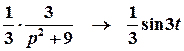 ;
; 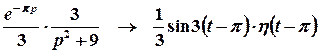 .
.
Тоді 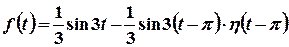 . Це означає, що для
. Це означає, що для 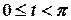
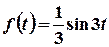 , а для
, а для 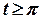
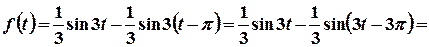
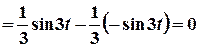 .
.
Остаточно 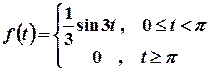 .
.
Приклад 3. Розв’язати за допомогою операційного метода задачу Коші
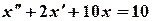 ,
, 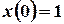 ,
, 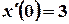 .
.
Розв’язок. Застосуємо до диференціального рівняння перетворення Лапласа. Позначимо як 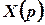 зображення шуканої функції
зображення шуканої функції 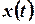 :
:
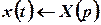 .
.
Тоді зображення похідних цієї функції можна побудувати за теоремою про диференціювання оригіналу:
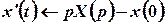 ,
, 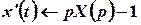 ;
;
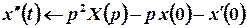 ,
, 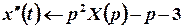 .
.
Зображення правої частини диференціального рівняння будується за допомогою таблиці зображень найпростіших функцій:
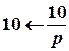 .
.
Тоді функція 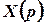 буде розв’язком операторного рівняння
буде розв’язком операторного рівняння
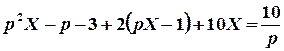 .
.
Розв’яжемо це рівняння.
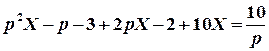 ;
;
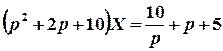 ;
;
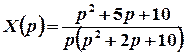 .
.
Знайдемо оригінал, який відповідає отриманому зображенню.
1 спосіб. Запишемо зображення 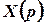 у вигляді суми функцій, оригінали для яких відомі:
у вигляді суми функцій, оригінали для яких відомі:
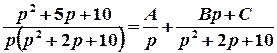 ;
;
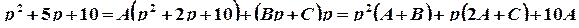 ;
;
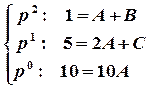 ;
; 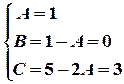 ;
;
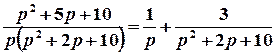 ;
; 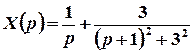 .
.
Тоді шуканий розв’язок задачі Коші дорівнює
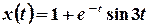 .
.
2 спосіб. Отримане зображення 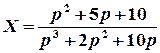 є правильним алгебраїчним дробом, отже, шуканий оригінал можна знайти за допомогою лишків:
є правильним алгебраїчним дробом, отже, шуканий оригінал можна знайти за допомогою лишків:
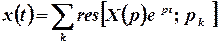 .
.
Особливі точки функції 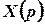 –
– 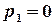 та
та 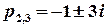 – є полюсами 1-го порядку, отже
– є полюсами 1-го порядку, отже
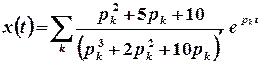 , або
, або 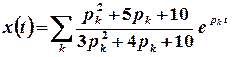 .
.
Полюс 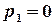 є дійсним, а полюси
є дійсним, а полюси 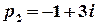 та
та 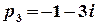 – комплексно спряжені, отже,
– комплексно спряжені, отже,
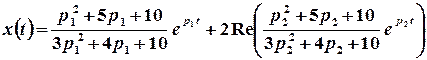 ;
;
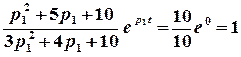 ;
;
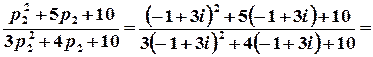
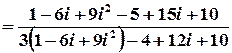
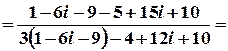
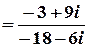
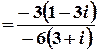
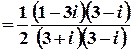
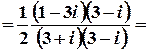
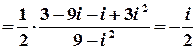 ;
;
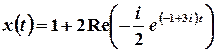
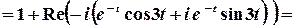
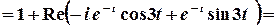
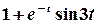 .
.
Остаточно, 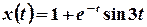 .
.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Дата: 2019-03-05, просмотров: 345.