Комплексним числом 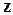 називається впорядкована пара дійсних чисел 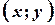. Число  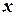називається дійсною частиною комплексного числа та позначається 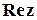,  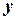називається уявною частиною та позначається 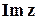. Операції додавання та множення комплексних чисел виконуються за такими правилами:

         ;

              .

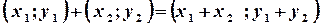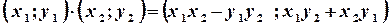    Будемо вважати, що дійсні числа є частинним випадком комплексних чисел. Якщо ототожнити дійсне число 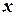 з комплексним числом  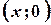та назвати пару  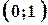числом  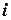– уявною одиницею, то число  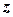можна записати у вигляді

              .

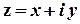    Така форма запису комплексного числа називається алгебраїчною, а дії додавання та множення з числами в алгебраїчній формі зводяться до стандартних перетворень з урахуванням рівності .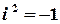

    Число 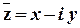 називається числом, спряженим до числа 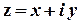. Добуток спряжених комплексних чисел є дійсним числом :

              .

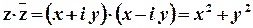    Ділення комплексних чисел виконується шляхом домноження числівника та знаменника дробу на число, спряжене до знаменника:

              .

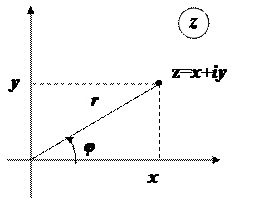
    Геометричним образом комплексного числа 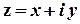 є точка на координатній площині з відповідними декартовими координатами. Полярні координати цієї точки також є важливими характеристиками комплексного числа. Відповідний полярний радіус називається модулем комплексного числа, а полярний кут – його аргументом:

              , .

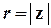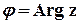    Дійсна та уявна частини комплексного числа зв’язані з його модулем та аргументом співвідношеннями , .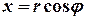

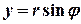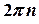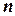    Як відомо, кожній точці координатної площини відповідає безліч значень полярного куту, які відрізняються одне від одного на , де  – ціле число.

    Для однозначного визначення аргументу комплексного числа будемо обирати його з певного проміжку довжиною 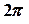. Таке значення аргументу називається його головним значенням та позначається 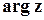. Будемо вважати, що  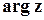належить проміжку  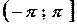(досить часто також використовують проміжок  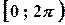).Тоді модуль та головне значення аргументу комплексного числа доцільно обчислювати за формулами

     ;

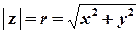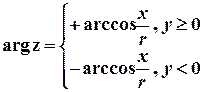або     .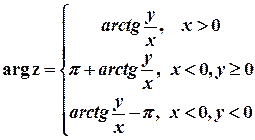

    З урахуванням наведених вище співвідношень комплексне число можна представити у вигляді

              .

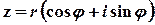    Така форма запису комплексного числа називається тригонометричною, а множення, ділення та піднесення до натурального степеня виконуються за формулами

              ;

              ;

              .

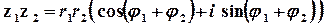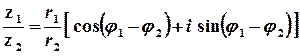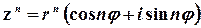З урахуванням формули Ейлера 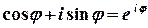 комплексне число може бути записано у показниковій формі

              .

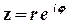    Якщо комплексні числа записані у показниковій формі, то дії множення, ділення та піднесення до натурального степеня виконуються за правилами

              ;

              ;

              .

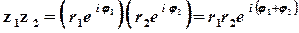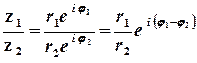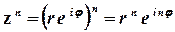    Коренем 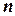-го степеня з комплексного числа  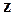називається таке число, 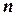-ий степінь якого дорівнює 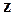. Обчислення кореня виконується за формулою

,    ,

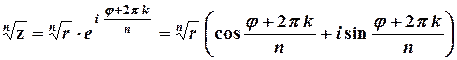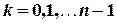тобто корінь 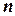-го степеня має  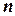значень.

Функції комплексної змінної

    Якщо задано закон 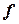, згідно з яким кожному значенню 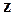, яке належить множині 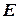, відповідає певне значення 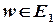, то кажуть, що задана однозначна функція 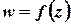, яка визначена на  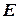та набуває значень в 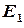. Якщо значенню  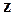відповідає декілька значень 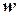, то функція є багатозначною.

    Функцію комплексної змінної можна записати у вигляді

              ,

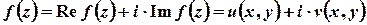де 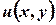 та 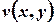 – функції дійсних змінних  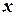та .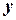

    Існування границі функції комплексної змінної 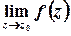 еквівалентне одночасному існуванню границь дійсної та уявної частин  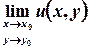та 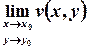. Аналогічно неперервність функції  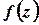у точці  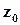еквівалентна неперервності функцій  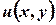та 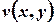у точці .

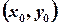    Функція, неперервна у кожній точці області , називається неперервною у цій області.

    Елементарні функції комплексної змінної. Введемо показникову функцію комплексної змінної 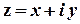 за правилом

.

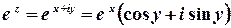    Тригонометричні та гіперболічні функції зв’язані з показниковою співвідношеннями

    ;   ; ;  ;

. ; .

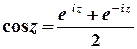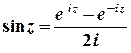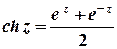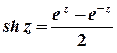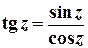
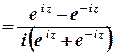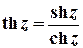
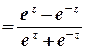Функції, які введені за цими формулами, по-перше, для дійсних значень аргумента 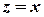 співпадають з відповідними функціями дійсної змінної, та, по-друге, зберігають всі властивості функцій дійсної змінної.

Також є очевидними властивості

    ;   ;   ; .

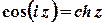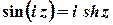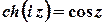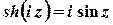    Функції 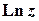, , 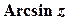,  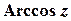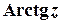визначають як обернені до функцій 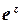, , 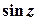,  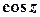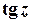відповідно. Зокрема,

               , ,

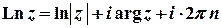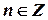а головне значення логарифмічної функції визначається як

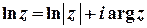(величина  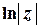є функцією дійсного аргументу).