Розглянемо послідовність комплексних чисел 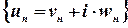 та побудуємо ряд
та побудуємо ряд 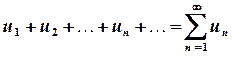 . Частковою сумою цього ряду називається сума
. Частковою сумою цього ряду називається сума 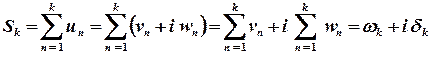 .
.
Якщо існують скінченні границі 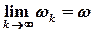 та
та 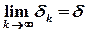 , то величина
, то величина 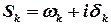 також має скінченну границю
також має скінченну границю 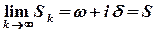 , ряд
, ряд 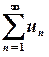 називається збіжним, а число
називається збіжним, а число 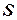 – сумою цього ряду.
– сумою цього ряду.
Ряд 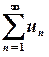 називається абсолютно збіжним, якщо збігається ряд
називається абсолютно збіжним, якщо збігається ряд 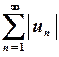 .
.
Необхідна умова збіжності. Якщо ряд 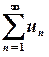 збігається, то
збігається, то 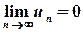 .
.
Наслідок. Якщо 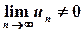 , то ряд
, то ряд 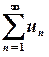 розбігається.
розбігається.
Ознака збіжності Даламбера. Нехай 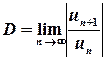 . Тоді, якщо
. Тоді, якщо 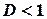 , ряд є абсолютно збіжним, а якщо
, ряд є абсолютно збіжним, а якщо 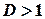 , то
, то 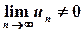 та ряд розбігається.
та ряд розбігається.
Ознака збіжності Коші. Нехай 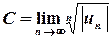 . Тоді, якщо
. Тоді, якщо 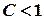 , ряд є абсолютно збіжним, а якщо
, ряд є абсолютно збіжним, а якщо 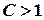 , то
, то 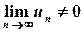 та ряд розбігається.
та ряд розбігається.
Функціональний ряд структури 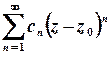 називається степеневим. Область збіжності такого ряду (тобто множину всіх значень змінної, для яких збігається відповідний числовий ряд) складають внутрішні точки кругу збіжності
називається степеневим. Область збіжності такого ряду (тобто множину всіх значень змінної, для яких збігається відповідний числовий ряд) складають внутрішні точки кругу збіжності 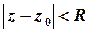 , та, можливо, деякі або всі точки кола
, та, можливо, деякі або всі точки кола 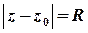 , яке обмежує цей круг. У внутрішніх точках круга збіжності ряд є абсолютно збіжним, ззовні кола ряд розбігається. Радіус збіжності
, яке обмежує цей круг. У внутрішніх точках круга збіжності ряд є абсолютно збіжним, ззовні кола ряд розбігається. Радіус збіжності 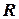 обчислюється за формулами
обчислюється за формулами
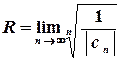 або
або 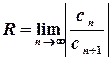 .
.
Круг збіжності можна також можна знайти безпосередньо з умов 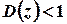 або
або 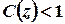 , де
, де 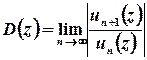 та
та 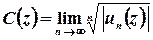 .
.
Розвинення функцій в ряди Тейлора та Лорана.
Особливі точки. Лишки
Функція 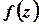 , аналітична у внутрішніх точках круга
, аналітична у внутрішніх точках круга 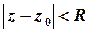 , може бути представлена у цьому крузі збіжним степеневим рядом
, може бути представлена у цьому крузі збіжним степеневим рядом 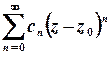 , який називається рядом Тейлора.
, який називається рядом Тейлора.
Для елементарних функцій комплексної змінної зберігаються розвинення у ряди Тейлора та Маклорена, отримані для функцій дійсної змінної:
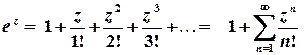 ,
, 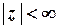 ;
;
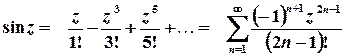 ,
, 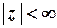 ;
;
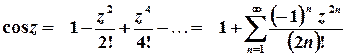 ,
, 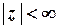 ;
;
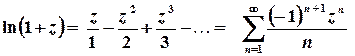 ,
, 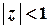 ;
;
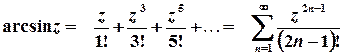 ,
, 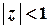 ;
;
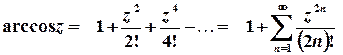 ,
, 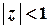 тощо.
тощо.
Якщо функція 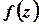 є аналітичною у кільці
є аналітичною у кільці 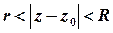 , то вона може бути представлена у точках цього кільця своїм рядом Лорана
, то вона може бути представлена у точках цього кільця своїм рядом Лорана
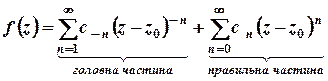 ,
,
де 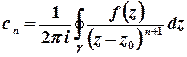 ,
, 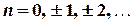 , інтегрування виконується вздовж кола
, інтегрування виконується вздовж кола 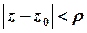 ,
, 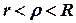 .
.
Радіуси 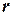 та
та 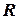 зв’язані з коефіцієнтами Лорана співвідношеннями
зв’язані з коефіцієнтами Лорана співвідношеннями
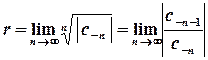 та
та 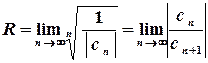 .
.
Точка 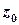 називається ізольованою особливою точкою функції
називається ізольованою особливою точкою функції 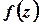 , якщо
, якщо 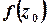 не визначена, та існує окіл
не визначена, та існує окіл 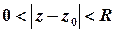 , в якому функція
, в якому функція 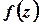 є аналітичною. Особлива точка
є аналітичною. Особлива точка 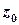 називається
називається
– усувною, якщо існує скінчений 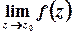 ;
;
– полюсом, якщо 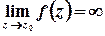 ;
;
– істотно особливою точкою, якщо 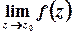 не існує.
не існує.
Число 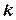 називається порядком нуля функції
називається порядком нуля функції 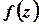 в точці
в точці 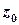 , якщо функція
, якщо функція 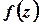 аналітична в точці
аналітична в точці 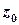 ,
, 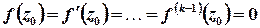 , та
, та 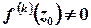 . Якщо точка
. Якщо точка 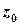 є нулем порядку
є нулем порядку 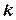 для функції
для функції 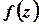 , то вона є полюсом порядку
, то вона є полюсом порядку 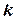 для функції
для функції 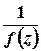 . Зокрема, число
. Зокрема, число 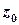 є полюсом порядку
є полюсом порядку 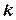 для функції
для функції 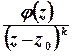 , якщо
, якщо 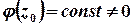 .
.
Якщо особлива точка 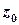 є усувною, всі коефіцієнти головної частини відповідного ряду Лорана дорівнюють нулю, у випадку полюса порядку
є усувною, всі коефіцієнти головної частини відповідного ряду Лорана дорівнюють нулю, у випадку полюса порядку 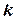 мають місце умови
мають місце умови 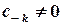 ,
, 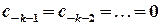 , нарешті, для істотно особливої точки існує нескінченна множина відмінних від нуля коефіцієнтів головної частини ряду Лорана.
, нарешті, для істотно особливої точки існує нескінченна множина відмінних від нуля коефіцієнтів головної частини ряду Лорана.
Лишком функції 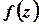 відносно скінченої точки
відносно скінченої точки 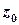 називається величина
називається величина
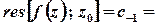
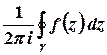 ,
,
де 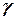 – будь-яке додатно орієнтоване коло
– будь-яке додатно орієнтоване коло 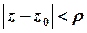 , яке лежить в кільці збіжності ряду Лорана.
, яке лежить в кільці збіжності ряду Лорана.
Якщо точка 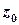 є точкою аналітичності функції
є точкою аналітичності функції 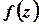 або її усувною особливою точкою, то
або її усувною особливою точкою, то 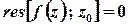 .
.
Лишок в простому полюсі обчислюють за формулами
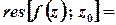
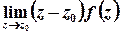 або
або
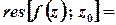
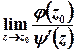 , де
, де 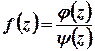 , причому
, причому 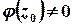 .
.
Якщо 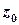 – кратний полюс порядку
– кратний полюс порядку 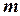 , то
, то
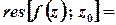
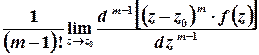 .
.
Для обчислення лишків в істотно особливих точках знаходять коефіцієнт 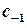 ряду Лорана інтегруванням або за допомогою відомих розвинень функцій у степеневі ряди.
ряду Лорана інтегруванням або за допомогою відомих розвинень функцій у степеневі ряди.
Основна теорема про лишки. Якщо функція 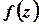 є аналітичною у замкненій області
є аналітичною у замкненій області 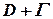 за винятком скінченої кількості особливих точок
за винятком скінченої кількості особливих точок 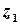 ,
, 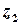 ,…
,… 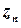 , які лежать усередині
, які лежать усередині 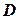 , то
, то
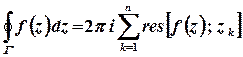 .
.
Операційне числення
Операційний метод – це специфічний спосіб розв’язування різних математичних задач, в першу чергу, диференційних рівнянь. Він базується на застосуванні інтегральних перетворень, зокрема, перетворення Лапласа, та складається з таких етапів:
1) від шуканої функції 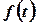 переходять до функції
переходять до функції 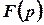 комплексної змінної, яку називають зображенням шуканої функції;
комплексної змінної, яку називають зображенням шуканої функції;
2) над зображенням виконують операції, які відповідають заданим операціям над шуканою функцією, – отримують так зване операторне рівняння для зображення 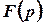 ;
;
3) операторне рівняння розв’язують відносно 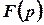 ;
;
4) від отриманого зображення 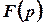 переходять до оригіналу, який є шуканою функцією.
переходять до оригіналу, який є шуканою функцією.
Дата: 2019-03-05, просмотров: 352.