Методами статистической обработки результатов исследования называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности.

В зависимости от применяемых методов можно охарактеризовать выборочное распределение данных исследования, можем судить о динамике изменения отдельных показателей, о статистических связях существующих между исследуемыми переменными величинами.

Математическая обработка результатов исследования дает психологу возможность ответить на ряд вопросов:

Чем один человек отличается от другого (или группы лиц) по исследуемой психологической характеристике?

Чем отличается уровень развития одной психологической характеристики от другой у данной личности?

Как развиваются две группы лиц по какой-либо психологической характеристике и др.

Ответы на эти и другие вопросы могут быть получены в ходе психодиагностического обследования и зависят от правильного проведения этого обследования, а также от грамотной обработки и интерпретации полученных результатов.

Главная цель статистических методов - представить количественные данные в сжатой форме, с тем, чтобы облегчить их понимание.

Все методы статистического анализа условно делятся на первичные и вторичные.

Первичными называются методы, с помощью которых можно получить показатели, непосредственно отражающие результаты проводимых в эксперименте измерений. Под первичными статистическими показателями имеются в виду показатели, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов диагностики.

К первичным методам статистической обработки относят: определение среднего арифметического, дисперсии, моды и медианы.

Вторичными называют методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности.

К вторичным методам статистической обработки относят: корреляционный анализ, регрессионный анализ, факторный анализ, методы сравнения первичных данных двух или нескольких выборок.

                        ПРАКТИЧЕСКАЯ ЧАСТЬ

1.Записать элементы множества A ={ x | x 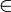 N;-3<x<11}.

Ответ: А={0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.

В каждый час первая труба наполняет 1/4 бассейна, а вторая – 1/3 бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы.

Дано:

I – 1/4 часть

                 } ?

II – 1/3 часть

 Решение:

 1/4 +1/3=3/12+4/12=7/12 ( обе трубы за 1 час)

Ответ: обе трубы за 1 час наполнят 7/12 бассейна.

Вычислите площадь круга, диаметр которого равен 4 см.

Дано:

d=4

 Найти - S

Решение:

Площадь круга S=πR², т.к. R= 1/2 d, следовательно  S=2²π=4 π

Ответ: S=4 π.

4. На складе было 2400 рулонов обоев. Одному магазину отправили 40% от общего количества рулонов, а остальные – во второй магазин. Сколько рулонов обоев отправили в первый и во второй магазины?

Дано:

I – 40%

                  } 2400 рул.

II – ? остальн.

Решение:

1) 2400 : 100 х 40=960 рул. (в 1-й магазин)

2) 2400 – 960 =1440 рул. (во 2-й магазин)

Ответ: в 1-й магазин отправили 960 рулонов обоев, во 2-й магазин – 1440 рулонов.

Представить число 2 5/14 в виде десятичной дроби. Округлить до сотых и найти абсолютную погрешность приближения ( D ).

Решение:

2 5/14= (28+5)/14 ≈ 2,3571 ≈2,36; абсолютная погрешность приближения(D):

2,3600-2,3571 ≈00029.

Два велосипедиста выехали навстречу друг другу. Первый ехал со скоростью 15 км/ч. Второй проехал до встречи на 6 км больше, чем первый. С какой скоростью ехал второй велосипедист, если он встретился с первым через 3 ч?

Дано:

I – 15 км/ч

                  } 3 ч.

II- ? на 6 км б.

Решение:

1) 15х3=45 км (проехал до встречи 1-й велосипедист)

2) 45+6=51 км (проехал 2-й велосипедист до встречи)

3) 51:3=17 км/ч (скорость 2-го велосипедиста)

Ответ: 2-й велосипедист ехал со скоростью 17 км/ч.

7.Изобразите при помощи кругов Эйлера а) В∩ СU А; б) С\ В ∩ А.