Планиметрия – это раздел геометрии, в котором изучаются фигуры на плоскости. Геометрическую фигуру определяют, как любое множество точек. Отрезок, прямая, круг – геометрические фигуры.

Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.

Основные свойства простейших фигур на плоскости выражаются в следующих аксиомах:

1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

Эта аксиома выражает основное свойство принадлежности точек и прямых на плоскости.

2. Из трех точек на прямой одна и только одна лежит между двумя другими.

Этой аксиомой выражается основное свойство расположения точек на прямой.

3. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Очевидно, что аксиома 3 выражает основное свойство измерения отрезков.

4. Прямая разбивает плоскость на две полуплоскости.

Этим предложением выражается основное свойство расположения точек относительно прямой на плоскости.

5. Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180^о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Эта аксиома выражает основное свойство измерения углов.

6. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

7. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180^О, и только один.

В этих аксиомах отражаются основные свойства откладывания углов и отрезков.

К основным свойствам простейших фигур относится и существование треугольника, равного данному.

8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой

Основные свойства параллельных прямых выражается следующей аксиомой.

9. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

МНОГОУГОЛЬНИКИ.

Многоугольник( n -угольник) — это геометрическая фигура, определяется как замкнутая ломаная.

Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.

Свойства многоугольника:

1) Сумма внутренних углов плоского выпуклого n-угольника равна.

2) Число диагоналей всякого n-угольника равно.

3) Произведение сторон многоугольника на синус угла между ними равна площади многоугольника.

8. ОКРУЖНОСТЬ. КРУГ.

Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)

Свойства окружности:

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Круг – это часть плоскости, ограниченная окружностью .Точка О также называется центром круга.

Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.

Полукруг (◓) - часть круга, которая ограничена полуокружностью и диаметром.

Сектор (◔) - часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Сегмент - часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.

Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.

a//b – читается как a параллельна b.

 Через точку, не ле­жа­щую на дан­ной пря­мой, про­хо­дит толь­ко одна пря­мая, па­рал­лель­ная дан­ной.

Если пря­мая пе­ре­се­ка­ет одну из па­рал­лель­ных пря­мых, то она пе­ре­се­ка­ет и дру­гую.

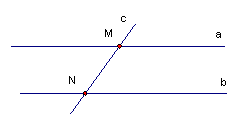
Если две пря­мые па­рал­лель­ны тре­тьей пря­мой, то они па­рал­лель­ны.

ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ.

Две прямые, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».

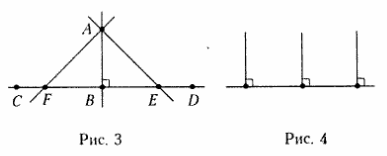
1. Через точку А (рис. 3) можно провести только одну перпендикулярную прямую АВ к прямой СD; остальные прямые, проходящие через точку А и пересекающие СD, называются наклонными прямыми (рис. 3, прямые АЕ и АF).

2. Из точки A можно опустить перпендикуляр на прямую CD; длина перпендикуляра (длина отрезка АВ), проведенного из точки А на прямую CD,— это самое короткое расстояние от A до CD (рис. 3).

3. Несколько перпендикуляров, проведенных через точки прямой к прямой, никогда между собой не пересекаются (рис. 4).