ПОДМНОЖЕСТВО. РАВНЫЕ МНОЖЕСТВА. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.
Подмножество - это множество, полностью входящее в другое множество.
Например, во множество всех людей входит подмножество женщин, подмножество негров, подмножество левшей и т. п.
Множество А равно множеству В (А=В), если все элементы множества А принадлежат множеству В и наоборот, все элементы множества В принадлежат множеству А.
Ни количество элементов, ни порядок их следования не имеет значения для равенства множества.
Пример: А={1; 2} и В={1, 2, 2, 1}, А=В
Операции над множествами
Результатом операций над множествами всегда является множество.
1. Пересечением множеств А и В (A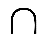 
B ) называется такое множество, которое состоит из элементов, принадлежащих множеству А и принадлежащих множеству В (т.е. их общих элементов). Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству.
2. Объединением множеств А и В (А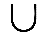 
В ) , называют такое множество, в которое входят элементы множества А или множества В (т.е. все элементы А и все элементы В).
3. Разностью множеств В и А (А\В) называют множество, которому принадлежат все те элементы множества В, которые не принадлежат А.
4. Дополнением множества А до множества В, называется такое множество, которому принадлежат все те элементы множества В, которые не принадлежат А. Пусть В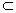 
А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В:
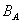'.= {x | x 
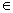A, x 
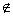B}.
Дополнением множества тупоугольных треугольников на плоскости до множества всех треугольников является множество остроугольных и прямоугольных треугольников. Найдем дополнение множества В = {1, 2, 3} до множества А ={1, 2, 3, 4, 5, 6, 7, 8}. Получим множество 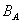'= {4, 5, 6, 7 ,8}.
ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВ.
Декартовым произведением множества А на множество В, называется множество всевозможных пар, первый элемент которых принадлежит множеству А, а второй - множеству В.
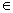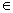А х В = {(а, в), а А, в В}.
Пара – упорядоченное множество, состоящее из двух элементов.
А= {1, 2}, В= {3, 4}, А х В= {(1, 3), (1, 4), (2, 3), (2, 4)}.
Пусть А= {1, 2, 3}, B={4, 5}. Образуем всевозможные пары (а;b) так, что а 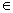А, b 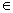В. Получим некоторое новое множество {(1; 5), (1; 4), (2; 4), (2; 5), (3; 4), (3; 5)}, элементами которого являются упорядоченные пары чисел. Это новое множество называют декартовым произведением множеств А и В.
МНОГОУГОЛЬНИКИ.
Многоугольник( n -угольник) — это геометрическая фигура, определяется как замкнутая ломаная.
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Свойства многоугольника:
1) Сумма внутренних углов плоского выпуклого n-угольника равна.
2) Число диагоналей всякого n-угольника равно.
3) Произведение сторон многоугольника на синус угла между ними равна площади многоугольника.
8. ОКРУЖНОСТЬ. КРУГ.
Окружность – это плоская замкнутая линия, все точки которой находятся на одинаковом расстоянии от некоторой точки (точки О), которая называется центром окружности.
(Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.)
Свойства окружности:
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Круг – это часть плоскости, ограниченная окружностью .Точка О также называется центром круга.
Расстояние от точки окружности до её центра, а также отрезок, соединяющий центр окружности с её точкой, называется радиусом окружности/круга.
Полукруг (◓) - часть круга, которая ограничена полуокружностью и диаметром.
Сектор (◔) - часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.
Сегмент - часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.
a//b – читается как a параллельна b.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
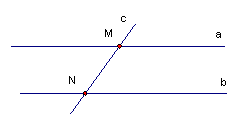
Если две прямые параллельны третьей прямой, то они параллельны.
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ.
Две прямые, пересекающиеся под прямым углом, называются перпендикулярными. Перпендикулярность прямых (или их отрезков) обозначают знаком перпендикулярности «⊥».
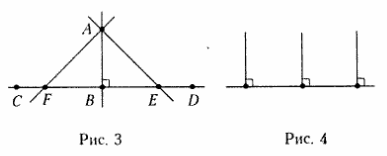
1. Через точку А (рис. 3) можно провести только одну перпендикулярную прямую АВ к прямой СD; остальные прямые, проходящие через точку А и пересекающие СD, называются наклонными прямыми (рис. 3, прямые АЕ и АF).
2. Из точки A можно опустить перпендикуляр на прямую CD; длина перпендикуляра (длина отрезка АВ), проведенного из точки А на прямую CD,— это самое короткое расстояние от A до CD (рис. 3).
3. Несколько перпендикуляров, проведенных через точки прямой к прямой, никогда между собой не пересекаются (рис. 4).
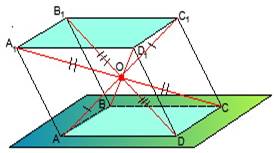
Свойства призмы
1о. Основания призмы являются равными многоугольниками.
2о. Боковые грани призмы являются параллелограммами.
3о. Боковые ребра призмы равны.
Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда
четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам.
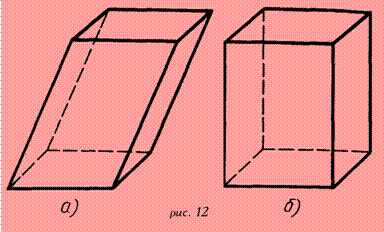
Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным. Диагональ прямоугольного параллелепипеда - d и его рёбра a, b, c связаны соотношением: d 2 = a 2+ b 2 + c 2.
Прямоугольный параллелепипед, все грани которого квадраты, называется кубом.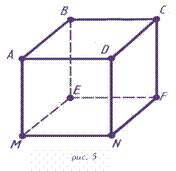 
Все рёбра куба равны.
Свойства параллелепипеда
1о. У параллелепипеда 8 вершин, 12 ребер и 6 граней.
2о. Каждая грань параллелепипеда — параллелограмм.
3о. Противолежащие грани параллелепипеда равны.
4о. Параллельные ребра параллелепипеда равны.
Пирамида – это многогранник, у которого одна грань (основание пирамиды ) – это произвольный многоугольник ( ABCDE, рис.80 ), а остальные грани ( боковые грани ) – треугольники с общей вершиной S, называемой вершиной пирамиды.
Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т. д. Треугольная пирамида является тетраэдром ( четырёхгранником ), четырёхугольная – пятигранником и т. д.
Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.
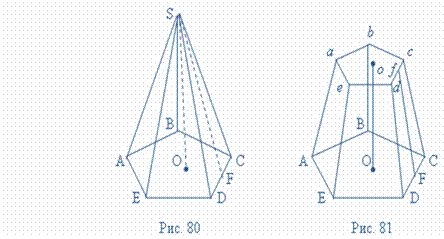
Если провести сечение abcde, параллельное основанию ABCDE (рис.81) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними – высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная. Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота Ff боковой грани
(рис.8) называется апофемой правильной усечённой пирамиды.
РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ.
Задачи на «движение».
Задачи на «работу».
Задачи на «работу».
Основными компонентами в задачах на работу являются: работа, производительность труда и время.
Производительность – это работа, выполненная за единицу времени (иначе, скорость работы).
Если обозначить через A – объем выполненной работы, p – производительность труда, t – время, то можно записать равенство:
A= p* t, которое называется формулой работы.
Из основной формулы получаем еще две: t= A/ p – формула для вычисления производительности (объем работы A и время ее выполнения t известны).
P= A/ t – формула для вычисления времени (если объем работы A и производительность труда p известны).
Все задачи на работу можно условно разделить на две группы:
-задачи, в которых выполняемый объем работы известен или его нужно определить (например, количество изготовленных деталей, количество га вспаханной земли, объем бассейна и т.д.); -
-задачи, в которых вообще не сказано, какая работа выполняется или эта работа задана неявно (в таких задачах зачастую задано только время).
Главное запомнить, что есть три фактора, а формулы можно вывести исходя из здравого смысла.
Два велосипедиста выехали навстречу друг другу. Первый ехал со скоростью 15 км/ч. Второй проехал до встречи на 6 км больше, чем первый. С какой скоростью ехал второй велосипедист, если он встретился с первым через 3 ч?
Дано:
I – 15 км/ч
} 3 ч.
II- ? на 6 км б.
Решение:
1) 15х3=45 км (проехал до встречи 1-й велосипедист)
2) 45+6=51 км (проехал 2-й велосипедист до встречи)
3) 51:3=17 км/ч (скорость 2-го велосипедиста)
Ответ: 2-й велосипедист ехал со скоростью 17 км/ч.
7.Изобразите при помощи кругов Эйлера а) В∩ СU А; б) С\ В ∩ А.
ПОНЯТИЕ МНОЖЕСТВА. ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ.
В математике часто рассматриваются те или иные группы объектов как единое целое: натуральные числа, треугольники, квадраты и т.д. Все эти различные совокупности называются множествами.
Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве гласных букв русского алфавита, о множестве натуральных чисел, о множестве треугольников.
Математический смысл слова «множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим числом предметов. В математике этого не требуется. Здесь можно рассматривать множество, состоящее из одного объекта, и множество, не со держащее ни одного объекта.
Множества принято обозначать прописными буквами латинского алфавита: А, В, С, ..., Z.
Множество, не содержащее ни одного объекта, называется пустым и обозначается символом ∅.
Объекты, из которых образовано множество, называются элементами.
Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c, ..., z.
В математике нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Например, мы говорим, что 5- число натуральное, а 0,75 не является натуральным числом. Другими словами, мы утверждаем, что число 5 принадлежит множеству натуральных чисел, а число 0,75 ему не принадлежит. Чтобы записать эти утверждения, вводятся символы E и E. Предложение «Объект а принадлежит множеству A» можно записать, используя символы: a {\displaystyle A\subset B}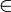 
A. Предложение «Объект а не принадлежит Множеству A» можно записать так: a 
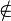А.
Например, если 4- множество однозначных чисел, то утверждение «Число 3- однозначное» можно записать в таком виде: 3 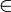А. Запись 12 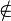А означает, что «Число 12 не является однозначным», или «Число 12 не принадлежит множеству A», или «Множество А не содержит числа 12».
Заметим, что в геометрии, которая возникла значительно раньше теории множеств, если точка является элементом какого-либо множества, то ее обозначают заглавной буквой. Например, если х- множество точек отрезка AB, то предложение «Точка Р лежит на отрезке AB» можно записать; P 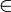X или P 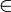AB.
Множества бывают конечные и бесконечные. Эти понятия мы принимаем без определения. Поясним их на примерах. Так, конечными являются множество дней недели, множество месяцев в году, а бесконечными - множество точек на прямой, множество натуральных чисел.
Для ряда числовых множеств в математике приняты стандартные обозначения:
N – множество натуральных чисел;
Z - множество целых чисел;
Q – множество рациональных чисел;
R- множество действительных чисел.
1. Отношение равенства
Говорят, что А=В, если все элементы множества А принадлежат множеству В и наоборот, все элементы множества В принадлежат множеству А.
Ни количество элементов, ни порядок их следования не имеет значения для равенства множества.
Пример: А={1; 2} и В={1, 2, 2, 1}, А =В.
2. Отношение включения
Говорят, что множество А включено ( 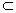) в В, если все элементы множества А принадлежат В.
В этом случае множество А будем называть подмножеством В.
Если А={1, 2}, В={1, 2, 3}, то А 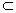В.
Если А - студенты дошфака, В - студенты университета, то А 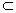В.
3. Отношение пересечения
Говорят, что множества А и В пересекаются, если имеют хотя бы один общий элемент.
Например, А={1, 2, 3} и В={2, 4, 6} , А и В - пересекаются.
А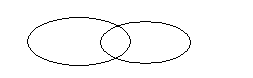 
В
Дата: 2019-03-05, просмотров: 447.
