1. Начертить структурную схему механизма.
2. Обозначит все подвижные звенья механизма.
3. Заглавными буквами латинского алфавита обозначить все кинематические пары и указать класс кинематической пары.
4. Определить степень подвижности механизма.
5. Удалить лишние степени свободы (если они есть).
6. Удалить пассивные связи (если они есть).
7. Заменить высшие кинематические пары на низшие.
8. Отсоединить от механизма группу Ассура 2-го класса (два звена), так чтобы: оставшийся механизм продолжал работать, а степень его подвижности (W) не менялась (оставалась прежней).
9. Если нельзя отсоединить группу Ассура 2-го класса, то отсоединить группу Ассура 3-го класса (четыре звена) так, чтобы: оставшийся механизм продолжал работать, а W не менялась.
10. Если нельзя отсоединить группу Ассура 3-го класса, то отсоединить группу Ассура 4-го класса, так, чтобы: оставшийся механизм продолжал работать, а W механизма не менялась.
11. Класс механизма определяем по наивысшему классу группы Ассура, входящей в состав механизма.
11. Вопросы для самопроверки.
1. Кто из выдающихся деятелей культуры эпохи Возрождения разработал проекты конструкций механизмов ткацких станков, печатных машин ?
Ответ: Леонардо да Винчи (1452-1519).
2. Действительный член Петербургской Академии наук XVIII века, автор 850 научных трудов, в том числе: «О машинах вообще» (1753 г) и «Принципы теории машин»?
Ответ: Леонард Эйлер (1707-1783).
3. Какой русский механик впервые разработал проект двухцилиндрового парового двигателя и осуществил в 1765 году его испытание?
Ответ: Ползунов Иван Иванович.
4. Именем какого русского ученого названа структурная формула плоских механизмов?
Ответ: Чебышев Пафнутий Львович.
5. “Отец русской авиации”, который был не только основоположником современной аэродинамики, но и автор целого ряда работ по прикладной механике и теории регулирования хода машин?
Ответ: Жуковский Николай Егорович.
6. Автор учебников, академик, организатор советской школы теории механизмов и машин, зав. кафедрой ТММ в МАИ ?
Ответ: Артоболевский Иван Иванович.
7. Что такое звено механизма? Ответ: твёрдое тело, состоящее из одной или нескольких деталей.
8. Что такое анализ механизма? Ответ: исследование структурных, кинематических или динамических свойств механизма.
9. Из чего состоит механизм?
Ответ: из отдельных звеньев.
10. Как называется каждая подвижная деталь или группа деталей, образующих одну жесткую систему тел в механизме?
Ответ: подвижное звено механизма.
11. Как называются неподвижные детали, которые образуют одну жесткую неподвижную систему тел в механизме?
Ответ: неподвижное звено (стойка).
12. Сколько неподвижных звеньев в механизме?
Ответ: 1.
13. Чем отличается механизм от кинематической цепи?
Ответ: наличием стойки.
14. Как называется соединение двух соприкасающихся звеньев, допускающее их относительное движение?
Ответ: кинематическая пара.
15. Как называется система звеньев, связанных между собой кинематическими парами?
Ответ: кинематическая цепь.
16. Чему равен максимальный класс кинематической пары?
Ответ: 5.
17. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 5?
Ответ: S = 6 - H = 6 - 5 = 1
18. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 4?
Ответ: S = 2
19. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 3?
Ответ: S = 3.
20. Чему равно число условий связи, если число степеней свободы звеньев кинематической пары равно 1?
Ответ: S = 5.
21. Назовите максимальное число условий связи?
Ответ: S=5.
22. Назовите максимальное число степеней свободы звена кинематической пары в относительном движении?
Ответ: H = 5.
23. Чему равно число степеней свободы, если число условий связи равно 1?
Ответ: H = 5, так как H = 6 - S.
24. Чему равно число степеней свободы, если число условий связи равно 2?
Ответ: H = 4.
25. Чему равно число степеней свободы, если число условий связи равно 4?
Ответ: H = 2.
26. Чему равно число степеней свободы, если число условий связи равно 5?
Ответ: H = 1.
27. Как называется кинематическая пара, если её звенья соприкасаются по поверхности?
Ответ: низшая кинематическая пара.
28. Как называется кинематическая пара, если её звенья соприкасаются по линии или в точке?
Ответ: высшая кинематическая пара.
29. Напишите формулу Чебышева П. Л.
Ответ: W = 3n-2p5-p4.
30. Как называется кинематическая цепь, степень свободы которой равна нулю?
Ответ: ферма.
31. Как влияют лишние степени свободы на закон движения ведомого звена и однозначность его перемещения?
Ответ: никак.
32. Напишите название кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости
Ответ: шар – плоскость.
33. Напишите класс кинематической пары, которая представляет собой шар, перекатывающийся со скольжением по плоскости.
Ответ: 1 класс.
34. Как называется кинематическая пара, представляющая собой цилиндр, лежащий на плоскости?
Ответ: высшая кинематическая пара 2-го класса.
35. Напишите формулу Сомова-Малышева.
Ответ: W=6n - 5p5 - 4p4 - 3p3 - 2p2 - p1.
36. Начертите условное изображение пары:
шар-плоскость.
37. Начертите условное изображение пары:
сферическая (шаровая).
38. Начертите условное изображение пары:
плоскостная.
39. Начертите условное изображение пары:
цилиндрическая.
40. Начертите условное изображение пары:
сферическая с пальцем.
41. Начертите условное изображение пары:
поступательная.
42. Начертите условное изображение пары:
вращательная.
43. Начертите условное изображение пары:
винтовая.
44. Как классифицируют кинематические пары?
Ответ: по числу S (условий связи). S = 6 – H.
45. Название пары, допускающей относительное вращательное движение звеньев вокруг оси?
Ответ: вращательная пара.
46. Название пары, допускающей лишь прямолинейное поступательное относительное движение звеньев?
Ответ: поступательная пара.
47. Название пары., допускающей независимые вращательное и поступательное относительные движения звеньев?
Ответ: цилиндрическая пара.
48. Название пары, допускающей три независимых относительных вращения звеньев, вокруг осей x, y, z.
Ответ: сферическая пара.
49. Как называется механизм, все подвижные звенья которого движутся в параллельных плоскостях?
Ответ: плоский механизм.
50. Как называется механизм, подвижные звенья которого описывают траектории, лежащие в пересекающихся плоскостях?
Ответ: пространственный механизм.
51. Что произойдет, если S=6?
Ответ: кинематическая пара становится жестким соединением деталей, т.е. одним звеном.
52. Что произойдет, если S=0?
Ответ: пары не существует, а имеются 2 тела, движущихся независимо друг от друга.
53. Что представляет собой механизм 1-го класса?
Ответ: это механизм, состоящий из подвижного звена и стойки.
54. Чему равно число механизмов 1-го класса в механизме?
Ответ: число механизмов 1-го класса равно числу степеней свободы механизма.
55. Как называется звено, совершающее полный оборот вокруг неподвижной оси?
Ответ: кривошип.
56. Как называется подвижное звено (вращающееся, качающееся или движущееся возвратно-поступательно), которое является направляющей ползуна?
Ответ: кулиса.
57. Что такое группа Ассура?
Ответ: это кинематическая цепь с нулевой степенью подвижности, которая не распадается на более простые кинематические цепи, также обладающие нулевой степенью подвижности.
58. Какое число звеньев должно быть в группе Ассура?
Ответ: чётное (2 или 4).
59. На что подразделяются группы Ассура?
Ответ: на классы, порядки и виды
60. Чем определяется порядок групп Ассура?
Ответ: числом элементов, которыми она присоединяется.
61. В каком году Ассур сформулировал принцип образования плоских механизмов?
Ответ: 1914г.
62. Для каких механизмов подходит формула Чебышева для подсчёта степени подвижности?
Ответ: для плоских.
63. Что можно определить при помощи следующей формулы:
W = 3n – 2p5 – р4?
Ответ: степень подвижности плоского механизма.
64. В каких механизмах все звенья перемещаются в одной или параллельных плоскостях?
Ответ: в плоских.
65. В каких механизмах звенья перемещаются в пересекающихся плоскостях?
Ответ: в пространственных.
66. Что в формуле Чебышева обозначается как р4?
Ответ: число кинематических пар 4-го класса.
67. Что в формуле Чебышева обозначается как р5?
Ответ: число кинематических пар 5-го класса.
68. Что определяет формула Сомова-Малышева?
Ответ: степень подвижности пространственного механизма.
69. Как определить число кинематических пар в сложном шарнире?
Ответ: подсчитать число соединяемых звеньев (подвижных и неподвижных) и вычесть единицу.
70. Что изучает ТММ?
Ответ: строение, кинематику и динамику машин и механизмов при их анализе и синтезе.
71. Что такое машина?
Ответ: устройство для преобразования энергии, информации и материала.
72. Что такое механизм?
Ответ: система звеньев, которая предназначена для преобразования одного движения в другое.
73. Какое звено называется шатун?
Ответ: звено, совершающее сложное плоско параллельное движение.
74. Какое звено называется ползун?
Ответ: звено, совершающее поступательное прямолинейное движение.
75. Какое звено называется коромысло?
Ответ: звено, которое совершает неполный оборот вокруг оси, связанной со стойкой.
76. Чем отличается звено механизма от детали механизма?
Ответ: звено механизма состоит из одной или нескольких деталей.
77. Какое звено называется стойкой?
Ответ: неподвижные детали, которые образуют одну жесткую неподвижную систему тел в механизме.
78. Что такое кинематическая цепь?
Ответ: система звеньев, связанных между собой кинематическими парами.
79. Что такое кинематическая пара?
Ответ: подвижное соединение двух соприкасающихся звеньев.
80. Сколько классов кинематических пар Вы знаете?
Ответ: пять классов.
81. Напишите алгоритм определения класса кинематической пары.
Ответ: подсчитать число простейших движений, которыми обладает звено кинематической пары в относительном движении; вычесть полученное число из шести, получив при этом число связей, налагаемых данной кинематической парой на относительное движение её звеньев, и этим определим класс пары.
82. определите класс кинематической пары, образованной звеньями: шар – плоскость.
Ответ: S = 6 – H = 6 – 5 = 1, 1 класс.
83. определите класс кинематической пары, образованной звеньями: плоскость – цилиндр.
Ответ: S = 6 – H = 6 – 4 = 2, 2 класс.
84. Алгоритм замены высшей кинематической пары на низшую.
Ответ: проводим нормаль через точку касания кривых и отмечаем на ней центры кривизны кривых, образующих вращательные пары, в которых соединяются условные звенья.
85. С какой целью удаляют из механизма пассивные связи?
Ответ: чтобы упростить механизм, так как пассивные связи не оказывают никакого влияния на характер движения механизма.
86. С какой целью удаляют из механизма лишние степени свободы?
Ответ: чтобы упростить механизм.
87. С какой целью конструктора применяют в механизмах пассивные связи?
Ответ: для повышения его жесткости или для устранения неопределенности движения звеньев в некоторых положениях.
88. С какой целью конструктора применяют в механизмах лишние степени свободы?
Ответ: для уменьшения сил трения и износа звеньев.
89. Принцип образования плоских механизмов.
Ответ: последовательное присоединение кинематических цепей, являющимися группами Ассура.
90. Что такое механизм первого класса?
Ответ: это механизм с одной степенью свободы, состоящий из стойки и подвижного звена.
91. Алгоритм структурного анализа механизма.
Ответ: Построить кинематическую схему механизма. Обозначить все подвижные звенья механизма. Заглавными буквами латинского алфавита обозначить все кинематические пары и класс кинематической пары. Удалить лишние степени свободы (если они есть). Удалить пассивные связи (если они есть). Определить степень подвижности механизма. Заменить высшие кинематические пары на низшие. Отсоединить от механизма группу Ассура 2-го класса (два звена) так, чтобы: оставшейся механизм продолжал работать, а W не менялась. Если нельзя отсоединить группу Ассура 2-го класса, то отсоединить группу Ассура 3-го класса (четыре звена) так, чтобы: оставшейся механизм продолжал работать, а W не менялась. Если нельзя отсоединить группу Ассура 3-го класса, то отсоединить группу Ассура 4-го класса, так, чтобы: оставшейся механизм продолжал работать, а W механизма не менялась.
92. Цель структурного анализа механизма.
Ответ: определить класс механизма.
93. Алгоритм определения степени подвижности плоского механизма по формуле Чебышева.
Ответ: определить число подвижных звеньев, определить число кинематических пар, определить среди них высшие и низшие, посчитать по формуле Чебышева степень подвижности.
94. Нарисуйте группу Ассура 4го класса.
Ответ: 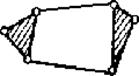
95. Нарисуйте группу Ассура 3го класса.
Ответ:
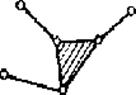
96. Нарисуйте группу Ассура 2го класса, 1го вида.
Ответ: 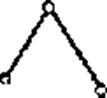
97. Нарисуйте группу Ассура 2го класса, 2го вида.
Ответ: 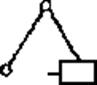
98. Нарисуйте группу Ассура 2го класса, 3го вида.
Ответ: 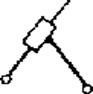
99. Нарисуйте группу Ассура 2го класса, 4го вида.
Ответ:
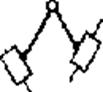
100. Нарисуйте группу Ассура 2го класса, 5го вида.
Ответ: 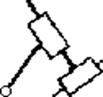
101. Как определяется класс механизма.
Ответ: по максимальному классу группы Ассура, входящей в механизм.
102. Назовите машины, с которыми Вы столкнетесь, работая по выбранной Вами специальности.
Ответ: двигатели внутреннего сгорания, гидротурбины и т.д.
103. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна 0.
Ответ: это значит, что ни одно звено не может двигаться относительно неподвижного звена, и кинематическая цепь превращается в ферму.
104. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна +2.
Ответ: это значит, что у механизма два ведущих звена.
105. Что это значит, если по формуле Чебышева Вы определили степень подвижности, и она равна –2.
Ответ:
106. Из скольких звеньев состоит группа Ассура 2го класса?
Ответ: 2.
107. Из скольких звеньев состоит группа Ассура 3го класса?
Ответ:4.
108. Из скольких звеньев состоит группа Ассура 4го класса?
Ответ:4.
109. Как определяется порядок группы Ассура?
Ответ: порядок равен числу поводков, которыми группа Ассура присоединяется.
12. Задачи для самостоятельного решения
(Провести структурный анализ механизма).
 Задача № 1.
Задача № 1.
 |







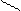





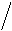



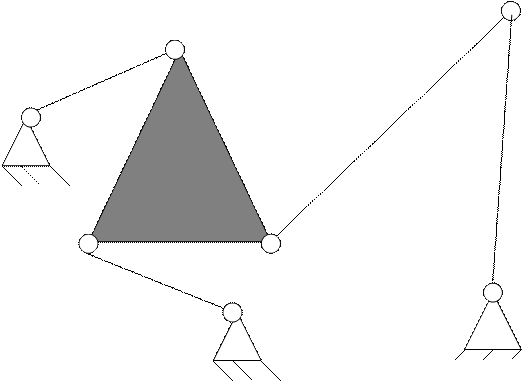
Задача № 2.
 |
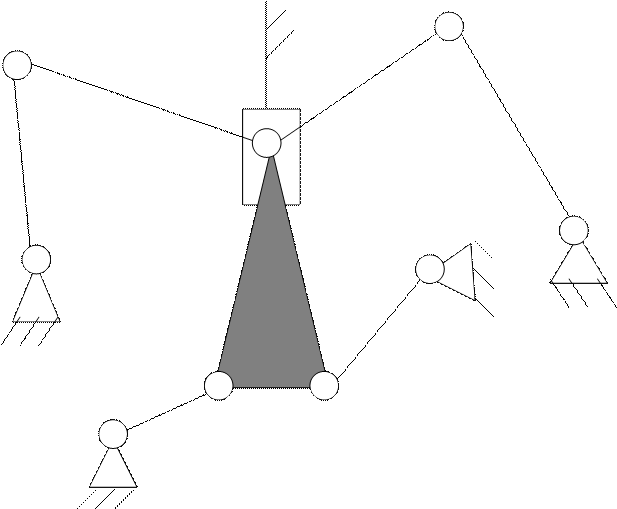
 Задача № 3.
Задача № 3.
 |
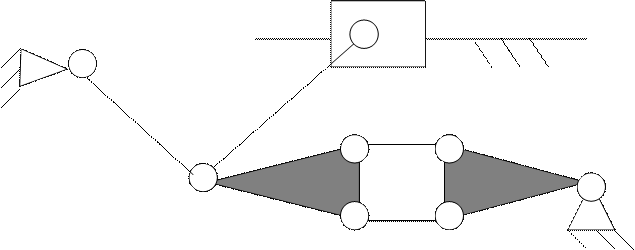
Задача № 4.
 |





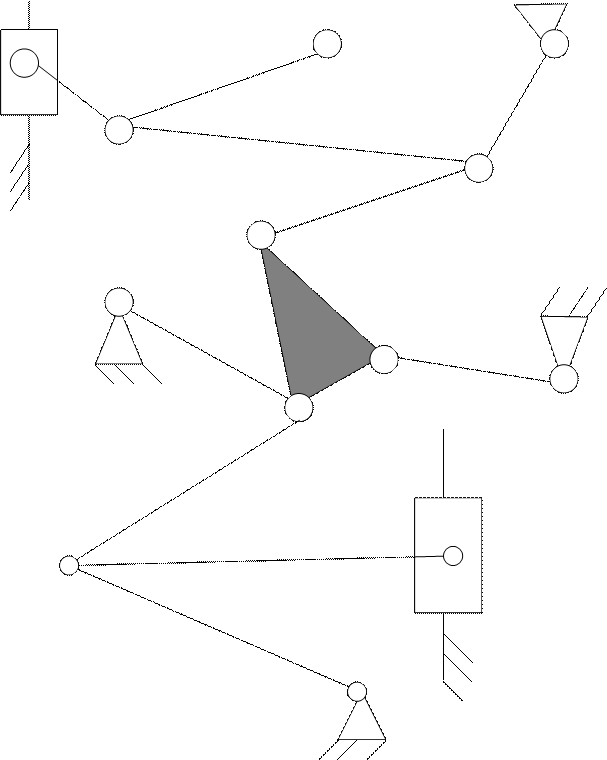
 Задача № 5.
Задача № 5.
 | |||
 | |||
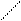
 Задача № 6.
Задача № 6.
 |













Примеры решения задач.
Цель: научиться проводить структурный анализ механизма.
Задача 1.
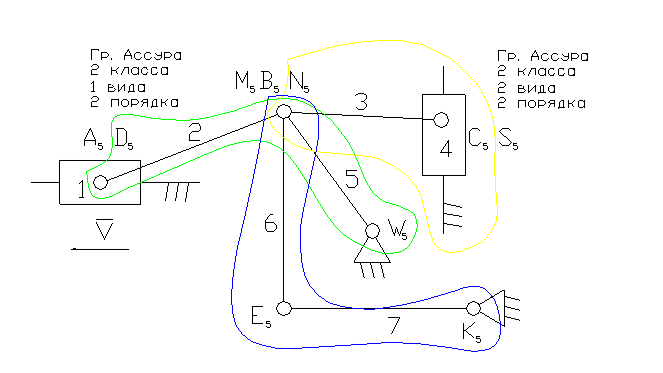
1 – ведущее звено ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1 – степень подвижности.
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем три группы Ассура 2 класса, состоящие из звеньев:
6,7; 2,5; 3,4. После отсоединения групп Асура остается ведущее звено 1 и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 2.
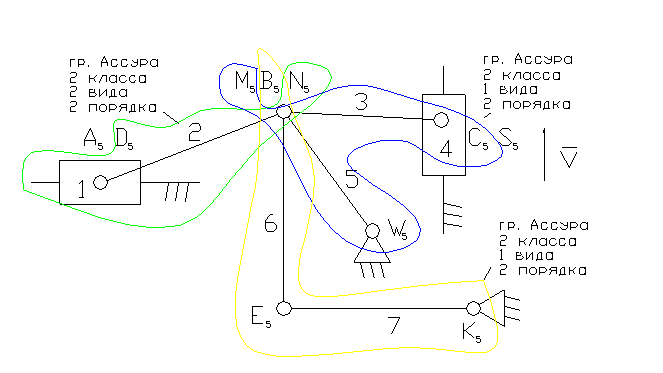
4 – ведущее звено ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, пвращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,5. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 3.
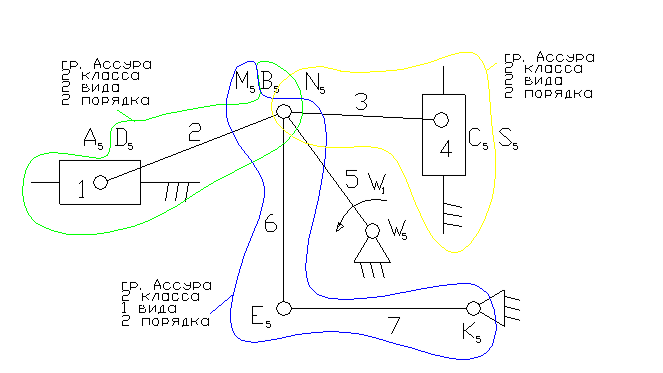
5 –ведущее звено – коромысло.
1 – ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Ассура входящий в состав механизма 2-й.
Задача 4.
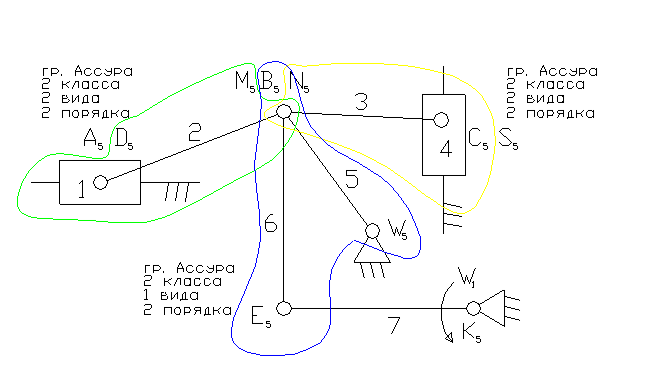
7- ведущее звено – коромысло.
1 – ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 6,5; 2,1; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Ассура входящий в состав механизма 2-й.
Задача 5.
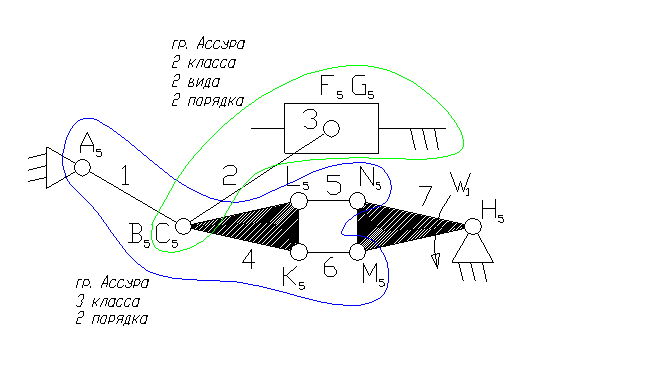 7 – ведущее звено – кривошип.
7 – ведущее звено – кривошип.
1– коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 1,4,5,6. Осталось ведущее звено и стойка.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 6.
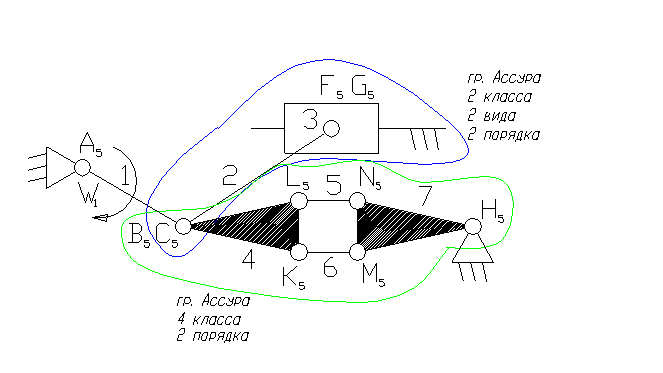
1– ведущее звено - коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
7 – кривошип.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9). Группы Ассура 3-го класса нет.
10) Отсоединяем группу Ассура 4-го класса, состоящую из звеньев 4,5,6,7. Осталось ведущее звено и стойка.
11). Класс механизма 4-й, т.к. наивысший класс группы Асура, входящий в состав механизма 4-й.
Задача 7.
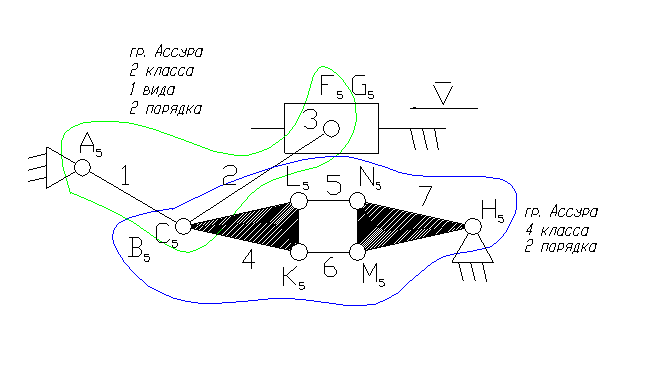
3- ведущее звено – ползун, совершает возвратно-поступательное движение.
1– коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
7- кривошип.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2.
9). Группы Ассура 3-го класса нет.
10). Отсоединяем группу Ассура 4-го класса, состоящую из звеньев 4,5,6,7. Осталось ведущее звено и стойка.
11). Класс механизма 4-й, т.к. наивысший класс группы Асура, входящий в состав механизма 4-й.
Задача 8.
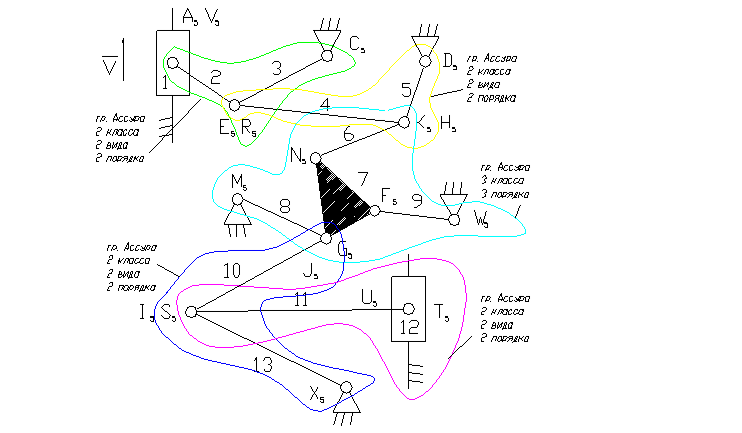 1 – ведущее звено ползун,
1 – ведущее звено ползун,
12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается),
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематическая пара 5-го класса низшие, поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13; 11,12.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 4,5 и 2,3.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 9.
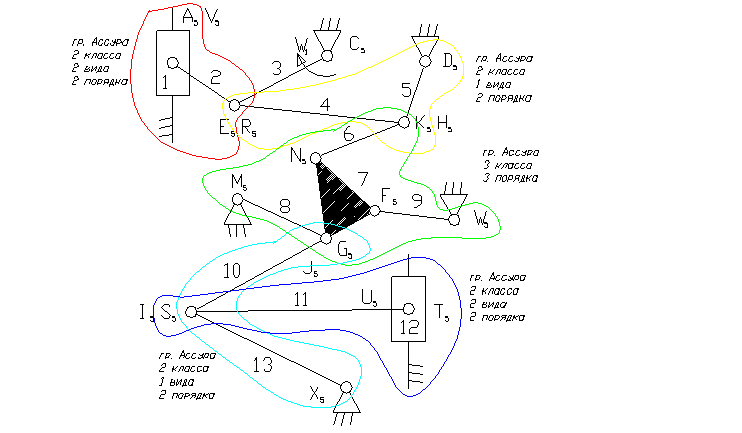
3 - ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3) A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4) W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5) Лишних степеней свободы нет.
6) Пассивных связей нет.
7) Высших кинематических пар нет.
8) Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13 и 11,12.
9) Отсоединяем группу Ассура 3-го класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 4,5 и 1,2.
Осталось ведущее звено и стойка.
11) Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 10.
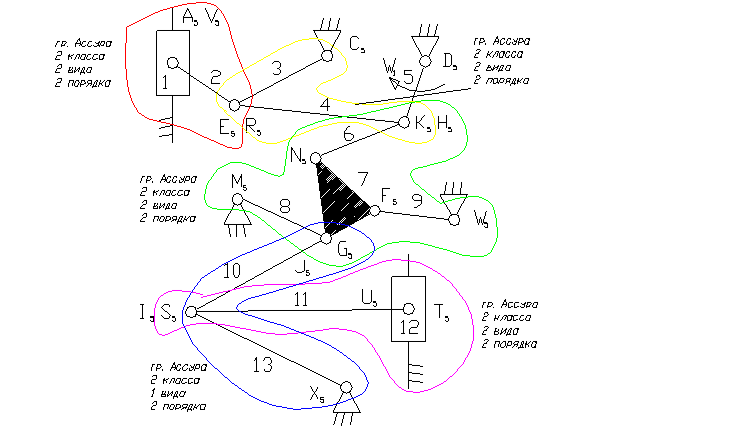
5 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3) A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4) W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5) Лишних степеней свободы нет.
6) Пассивных связей нет.
7) Высших кинематических пар нет.
8) Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13 и 11,12.
9) Отсоединяем группу Ассура 3-го класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 3,4 и 1,2.
Осталось ведущее звено и стойка.
11) Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 11.
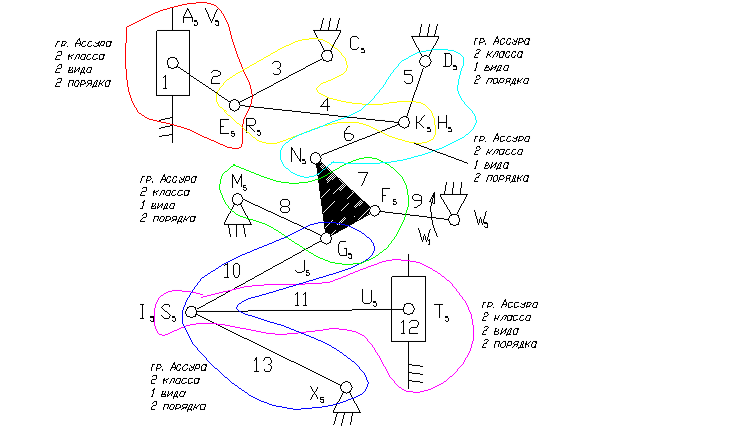
9 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 10,13; 11,12 и 7,8.
Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11) Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 12.
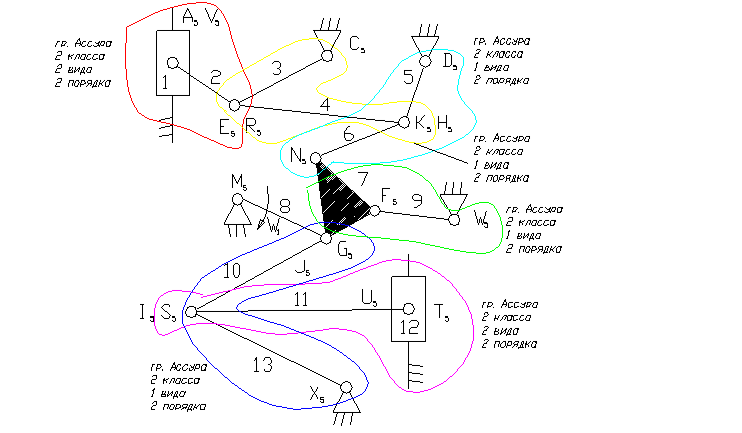
8 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 10,13; 11,12 и 7,9.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 13.
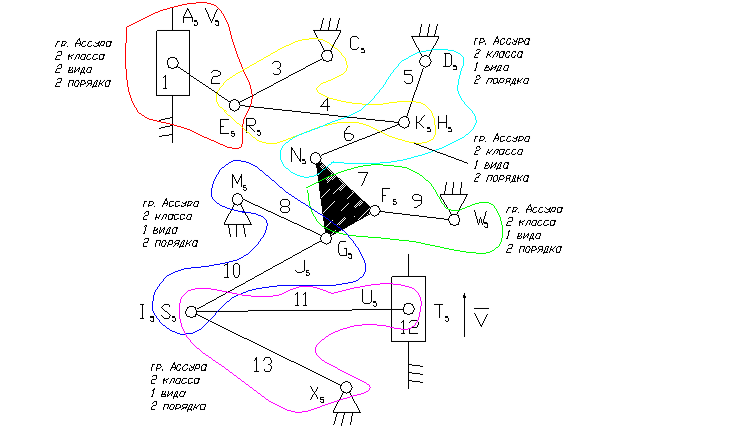 12 – ведущее звено ползун.
12 – ведущее звено ползун.
1, – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 7,9; 8,10; 11,13.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 14.
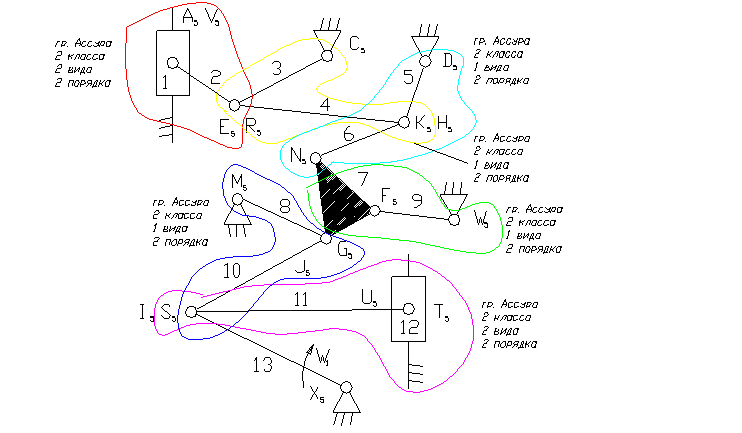
13 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 7,9; 8,10; 11,12.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 15.
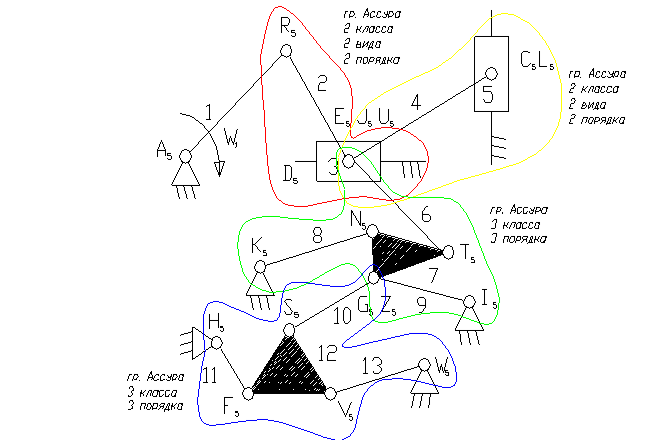
1 – ведущее звено кривошип – звено, которое совершает вращательное движение.
3, 5 – ползун.
8, 9, 11, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 16.
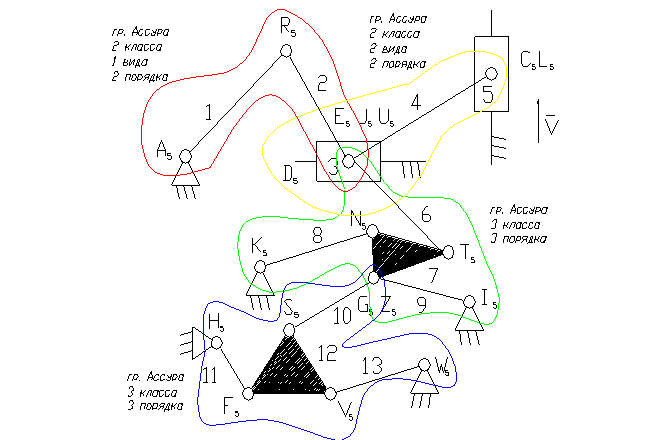
5 – ведущее звено ползун.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 3, 4.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 17.
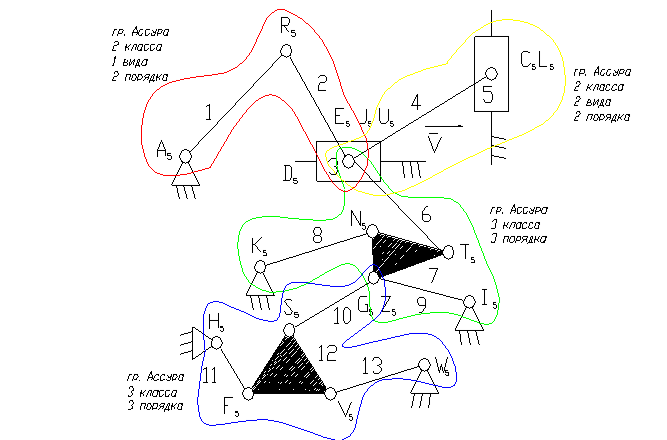 3 – ведущее звено ползун.
3 – ведущее звено ползун.
5 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун .
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2 и 4,5.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
Осталось ведущее звено и стойка.
10). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 18.
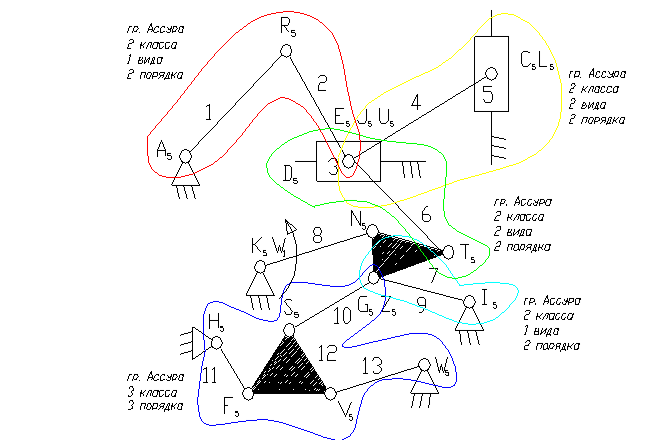 8 – ведущее звено коромысло.
8 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 7, 9.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 19.
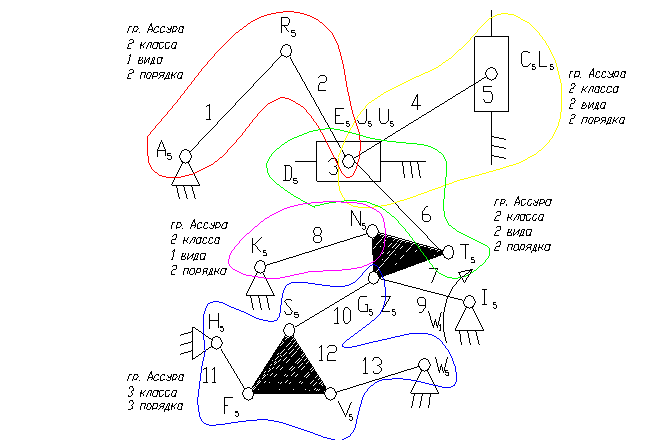 9 – ведущее звено коромысло.
9 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 7, 8.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 20.
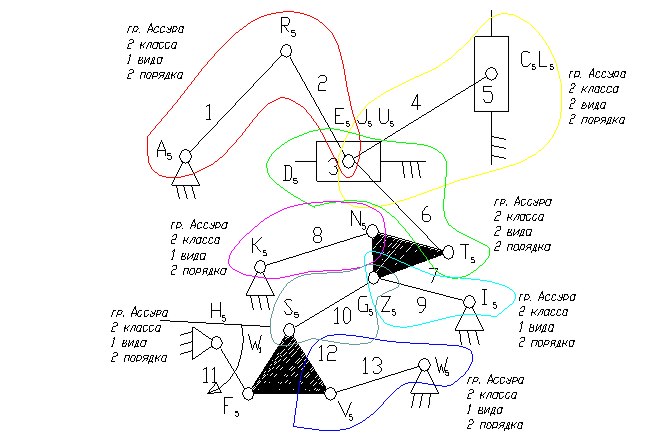
11 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6; 7,8; 9,10 и 12,13.
Осталось ведущее звено и стойка.
9). Класс механизма 2-ой, т.к. наивысший класс группы Асура, входящий в состав механизма 2-ой.
Задача 21.
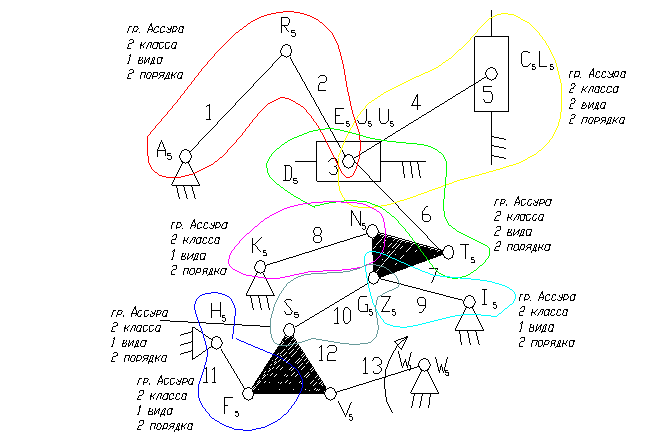
13 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6; 7,8; 9,10 и 11,12.
Осталось ведущее звено и стойка.
9). Класс механизма 2-ой, т.к. наивысший класс группы Асура, входящий в состав механизма 2-ой.
Задача 22.
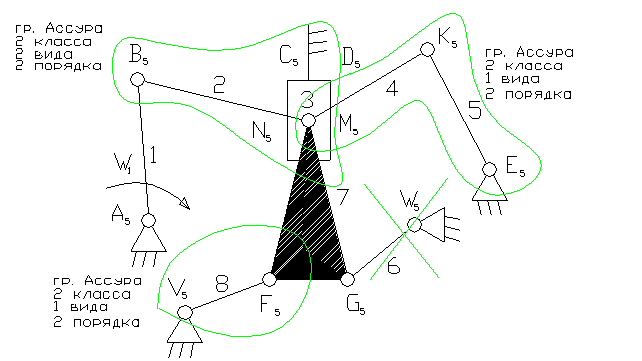 1- ведущее звено коромысло.
1- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
5, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5; 7,8; 2,3. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 23.
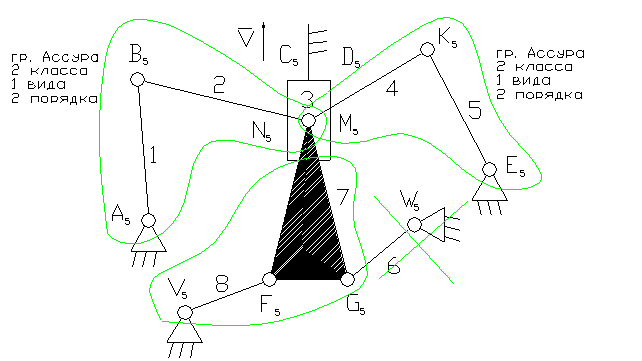
3- ведущее звено ползун.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 5, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5; 7,8; 1,2. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 24.
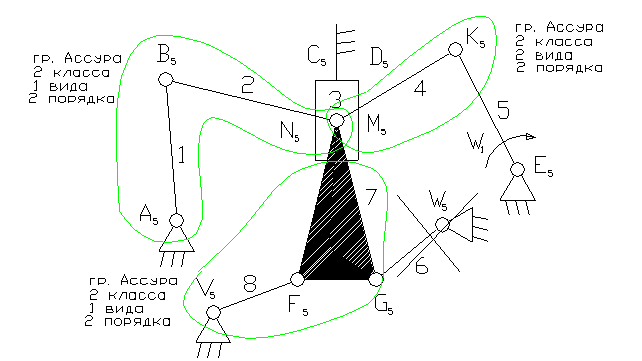
5- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 7,8; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 25.
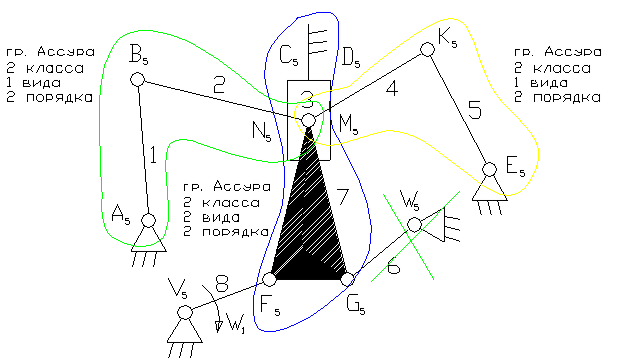
8- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 5, 6, – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,7. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Дата: 2019-03-05, просмотров: 473.