МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОУ ВПО Иркутский Государственный Технический Университет
ФТиКМ
Кафедра
Конструирования и стандартизации в машиностроении
П.В. Королев канд.техн.наук., доцент
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Конспект лекций
По дистанционному обучению
Иркутск 2010
Теория механизмов и машин. Конспект лекций по дистанционному обучению для студентов механических специальностей дневной, вечерней и заочной формы обучения высших технических учебных заведений. Составил: канд. техн. наук., доцент
П.В. Королев. – Иркутск, 2010. – …… с.
Представлен конспект лекций по предмету «Теория машин и механизмов». В конспекте отражены наименования тем, приведены рисунки, схемы, формулы и основные определения. Конспект лекций представляет собой методический материал для дистанционного обучения, который позволяет студенту:
- сократить время, затрачиваемое на выполнение чертежей, схем и написание формул,
- подробнее конспектировать материал лекции,
- изучать новый материал, «следить за мыслью лектора»,
- знать наименование будущих тем лекций и планировать свою подготовку к ним.
Для закрепления в памяти пройденного материала в конце каждой темы приведены вопросы для самопроверки с ответами и задачи для самостоятельного решения, подобные тем, которые встречаются на экзамене или зачете.
Конспект лекций по ТММ предназначен для студентов специальностей: АТ, СДМ, АС, ММ, СП, ЭЛ, СМ, ГМ, БТП, БЖТ дневной, вечерней и заочной формы обучения при изучении ими теоретической части курса и выполнении курсового проекта по теории механизмов и машин.
ОГЛАВЛЕНИЕ
ТЕМА 1: СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ……………
1. История развития ТММ.………………………………..
2. Вопросы, которые изучает ТММ ………………………
3. Основные понятия ТММ, термины и определения …..
4. Классификация кинематических пар ………………….
5. Степень подвижности плоских и пространственных
механизмов……………………………………………
6. Пассивные связи. Лишние степени свободы………..
7. Замена высших кинематических пар низшими……..
8. Принцип образования плоских механизмов…………
9. Классификация групп Ассура………………………...
10. Алгоритм проведения структурного анализа………..
11. Вопросы для самопроверки…………………………...
12. Задачи для самостоятельного решения………………
13. Примеры решения задач………………………………
ТЕМА 2: КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ…….
1. Цель и задачи кинематического анализа……………..
2. Масштабы в ТММ……………………………………...
3. Определение перемещений……………………………
4. Определение скоростей………………………………..
5. Определение ускорений……………………………….
6. Кинематические диаграммы…………………………..
7. Вопросы для самопроверки……………………………
8. Задачи для самостоятельного решения……………….
9. Примеры решения задач……………………………….
ТЕМА 3,4: ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА………..
1. Цель и задачи динамического анализа………………
ТЕМА 3: СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА……………………
1. Классификация сил в механизме…..…………………
2. Методы силового расчета механизма………………..
3. Порядок кинетостатического расчета механизма…..
4. Реакции в кинематических парах механизма……….
5. Порядок силового расчета группы Ассура………….
6. Порядок силового расчета ведущего звена…………
7. Теорема о жестком рычаге Жуковского…………….
8. Статическое уравновешивание вращающихся масс..
9. Вопросы для самопроверки…………………………..
10. Задачи для самостоятельного решения………………
11. Примеры решения задач………………………………
ТЕМА 4: ДИНАМИКА МЕХАНИЗМА…………………………….
1. Тахограмма механизма………………………………..
2. Коэффициент неравномерности хода механизма……
3. Кинетическая энергия механизма…………………….
4. Приведенная масса (приведенный момент
инерции) механизма………………………
5. Приведенная сила (приведенный момент)……………
6. Диаграмма Фердинанда Виттенбауэра……………….
7. Определение момента инерции маховика……………
8. Вопросы для самопроверки……………………………
9. Задачи для самостоятельного решения……………….
10. Примеры решения задач……………………………….
ТЕМА 5: МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ………………………….
1. Классификация механизмов передач…………………
2. Классификация зубчатых механизмов……………….
3. Многоступенчатые редуктора………………………...
4. Рядовое соединение зубчатых колес с (промежуточными)
паразитными колесами….. ……………………
5. Планетарные редуктора……………………………….
6. Вопросы для самопроверки…………………………..
7. Задачи для самостоятельного решения………………
8. Примеры решения задач………………………………
ТЕМА 6: ЭВОЛЬВЕНТНОЕ ЗАЦЕПЛЕНИЕ………………………
1. Основная теорема зацепления……………………….
2. Требования, предъявляемые к профилям зубьев
зубчатых колес: кинематические, динамические,
технологические, эксплуатационные…….…
3. Основные размеры нулевых зубчатых колес……….
4. Эвольвента окружности……………………………...
5. Ненулевые зубчатые колеса:
положительные и отрицательные……………
6. Методы выбора коэффициентов смещения
инструментальной рейки ……………
7. Коэффициент перекрытия (качественный
показатель зацепления)…………………
8. Таблица инволют……………………………………
9. Вопросы для самопроверки………………………..
10. Примеры решения задач……………………………
ТЕМА 7: КУЛАЧКОВЫЕ МЕХАНИЗМЫ……………………….
1. Особенности кулачковых механизмов…………….
2. Классификация кулачковых механизмов…………
3. Анализ кулачковых механизмов…………………..
4. Мягкие и жесткие удары…………………………...
5. Углы давления в кулачковых механизмах………..
6. Синтез кулачковых механизмов…………………..
7. Вопросы для самопроверки………………………..
8. Задачи для самостоятельного решения……………
9. Примеры решения задач……………………………
Контрольные вопросы к зачету и экзамену по курсу ТММ ………..
Список рекомендованной литературы……………………………………
Пример выполнения курсовой работы по ТММ………………………..
История развития ТММ.
Леонардо Да Винчи (1452 – 1519 г.)
 |
Леонард Эйлер (1707 – 1783 г.) Эвольвента
Чебышев Пафнутий Львович (1821 – 1894 г.)
W = 3n – 2p5 – p4
Сомов П.О. (1852- 1919 г.) и Малышев А.П. (1879-1962 г.)
W = 6n – 5p5 – 4p4 – 3p3 – 2p2 – p1
Р. Виллис (1800 – 1875 г.)
(j) (H)
U iH = 1 – U ij
i –подвижное колесо, j – неподвижное колесо, Н - водило
Ассур Леонид Владимирович (1878 – 1920 г.) – принцип образования плоских механизмов.
Леонардо да Винчи (1452 – 1519 г.): научное изучение рукописей началось более трех столетий спустя после смерти Леонардо, так как многое из того, что они заключали, не могло быть понято его современниками (шариковый подшипник, артиллерийские снаряды со стабилизатором, многоствольная скорострельная пушка и многое другое).
Эйлер Леонард (1707 – 1783 г.): в 1736 г. вышел его трактат по механике, принесший ему мировую славу. Выходят в свет его книги: «Интегральное исчисление», «Элементы алгебры», «Новая теория движения Луны», «Морская наука» и др. После себя Л. Эйлер оставил более 850 научных работ.
Ползунов Иван Иванович (1730-1766 г.): построил лесопильную мельницу, в которой подъем бревен и их подача были механизированы, сконструировал сооружения для подъема сплавных судов. В 1765 году было проведено успешное испытание паровой машины созданной Ползуновым, которая впервые в мире имела два цилиндра и рабочий вал. На создание паровой машины Екатерина 11 выделила 400 рублей, а доход, который приносила эта машина заводу составлял 440 рублей в сутки !
Кулибин Иван Петрович (1735-1818 г.): часовщик-изобретатель, создатель телескопов, первого в мире ахроматического микроскопа, электрических машин, термометра, оптического телеграфа, самодвижущаяся коляска (1791 г.), водоходное судно. Разработал теорию моделирования и расчета арочных мостов.
Чебышев Пафнутий Львович (1821 – 1894 г.): гениальный математик и механик. Сконструировал: оригинальные паровые машины, арифмометр, центробежный регулятор, самокатное кресло, лодку с гребным механизмом, стопоходящую машину и др. В работе «О параллелограммах» (1869 г.) Чебышев П.Л вывел структурную формулу плоского механизма:
W = 3 n – 2 p5 – p4.
Сомов Павел Осипович (1852-1919 г.): вывел структурную формулу пространственного механизма:
W = 6 n – 5 p5 – 4 p4 – 3 p3 – 2 p2 – p1 .
Жуковский Николай Егорович (1847-1921 г.): профессор Московского университета и Московского технического училища. Научные интересы Жуковского Н.Е. были многогранны: от аэромеханики (аэродинамика) и гидромеханики до исследования хвостов комет, общей теории устойчивости движения, теории регулирования машин, прочности велосипедного колеса, теории ветряных двигателей и др.
Леонид Владимирович Ассур (1878-1920 г.): профессор Петербургского политехнического института открыл закон образования плоских механизмов.
Артоболевский Иван Иванович, Колчин Н. И., Мовнин М. С., Кожевников С.Н.
Вопросы, которые изучает наука «ТММ».
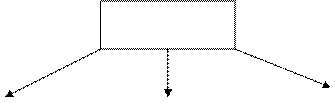
ТММ
Строение Кинематика Динамика
механизма механизма механизма
 |
Даны Найти Дан Найти
свойства. механизм. механизм. свойства.
Синтез Анализ
3. Основные понятия ТММ, термины и определения.
 |
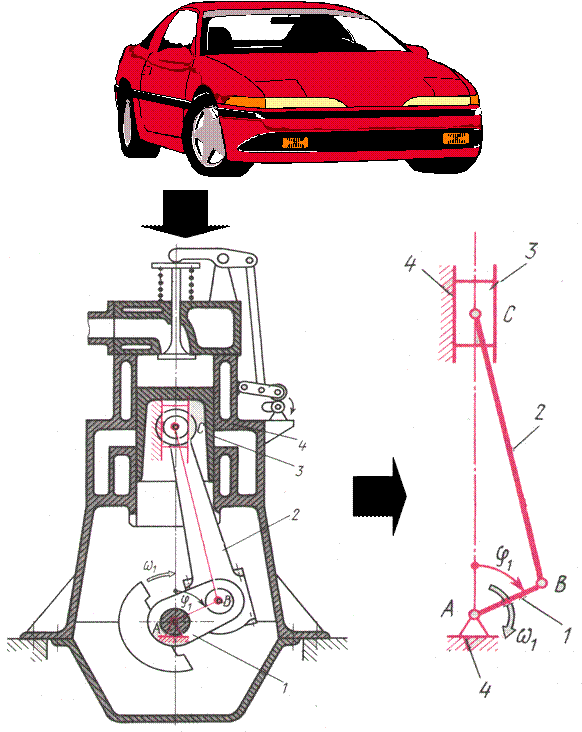Машина – это устройство, предназначенного для преобразования:
- энергии (двигатель внутреннего сгорания, турбина ),
- информации (ЭВМ),
- материалов (токарный станок, пилорама, пресс, кран).
Каждая машина состоит чаще всего из нескольких механизмов.
Механизм- это система тел, предназначенных для преобразования одного вида движения в другой вид движения, например: вращательное во вращательное, вращательное в возвратно-поступательное и т.д.
Механизм состоит из звеньев:
- стойка – неподвижное звено любого механизма,
- кривошип – совершает вращательное движение,
- шатун – совершает сложное плоско-параллельное движение,
- ползун – совершает возвратно-поступательное движение,
- коромысло (качающееся звено) – совершает неполный оборот вокруг оси,
- кулиса – звено, совершающее поступательное, вращательное или качательное движения, по которому перемещается ползун. В этом случае ползун называют камень кулисы.
Звенья в механизме соединяются между собой подвижным соединением. Подвижное соединение двух звеньев называется кинематической парой.
Если соединяются два звена, то будет одна кинематическая пара. Если соединяются три звена, то будет две кинематических пары. Если соединяются N звеньев, то будет N-1 кинематическая пара.
4. Классификация кинематических пар.
Кинематические пары
 |  |
Классы Группы
(Смотри с……)
Звено Звено
Подвижное
соединение
Класс кинематической пары = S (числу ограничений).
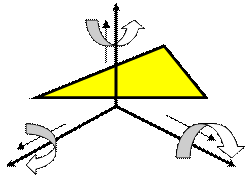Z
H = 6
S = 0
S - число ограничений
H – степень свободы
S = 6 - H
X Y
 |
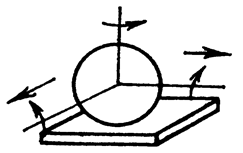1. Шар – плоскость: H = 5; S = 1; класс 1.
2. Шар – цилиндр: H = 4; S = 2; класс 2.
 |
 |
3. Сферическая: H = 3; S = 3; класс 3.
 |
 |
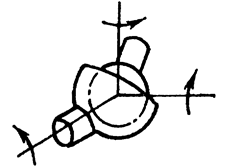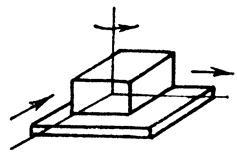4. Плоскостная: H = 3; S = 3; класс 3.
5.Цилиндрическая: H = 2; S = 4; класс 4.
 |
 |
6. Сферическая с пальцем: H = 2; S = 4; класс 4.
 |
 |
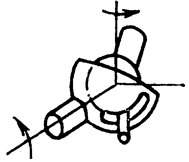7.Поступательная: H = 1; S = 5; класс 5.
 |
 |
 |
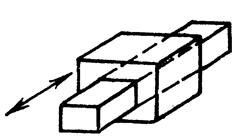8.Вращательная: H = 1; S = 5; класс 5.
 |
 |
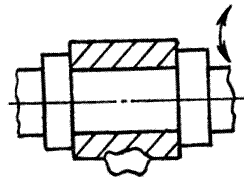9.Винтовая: H = 1; S = 5; класс 5.
 |
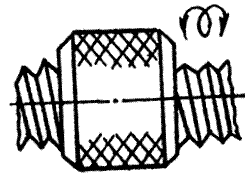Группы кинематических пар
Высшие кинематические пары – контакт между звеньями происходит по линии или в точке.
Низшие кинематические пары - контакт между звеньями происходит по поверхности.
Примеры решения задач.
Цель: научиться проводить структурный анализ механизма.
Задача 1.
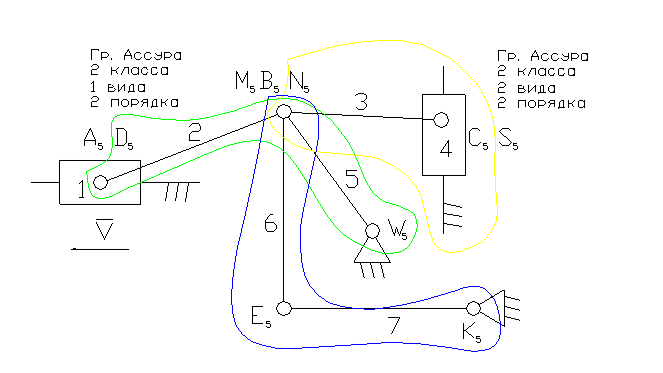
1 – ведущее звено ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1 – степень подвижности.
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем три группы Ассура 2 класса, состоящие из звеньев:
6,7; 2,5; 3,4. После отсоединения групп Асура остается ведущее звено 1 и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 2.
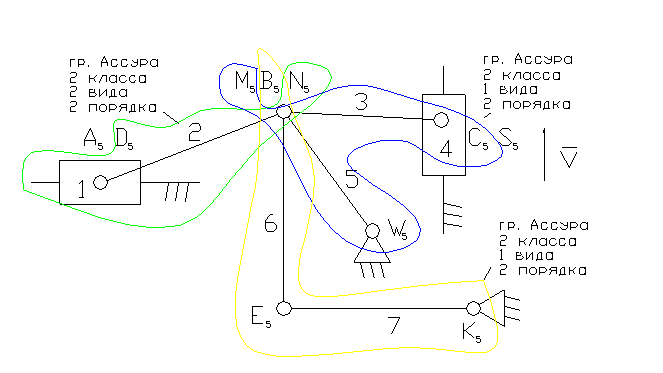
4 – ведущее звено ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, пвращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,5. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 3.
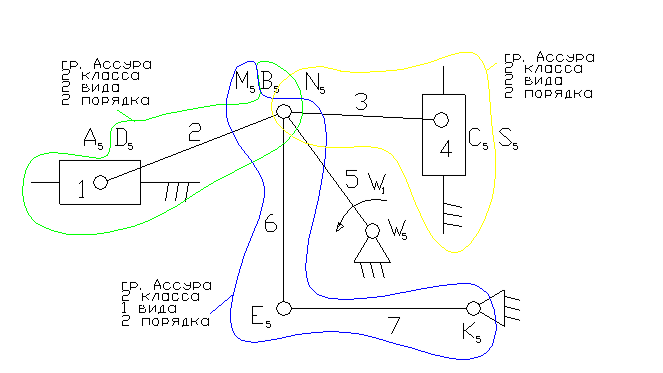
5 –ведущее звено – коромысло.
1 – ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группы Ассура 2 класса, состоящие из звеньев: 6,7; 2,1; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Ассура входящий в состав механизма 2-й.
Задача 4.
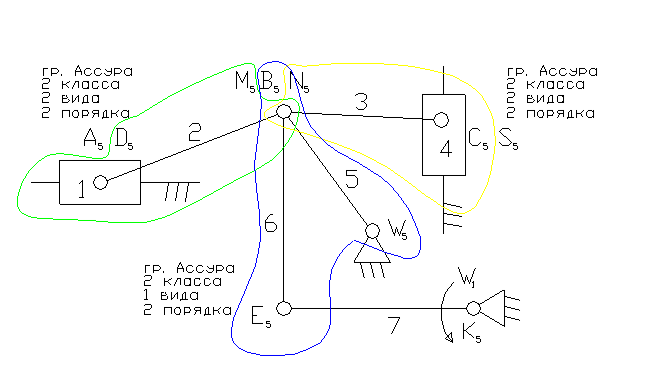
7- ведущее звено – коромысло.
1 – ползун – звено, которое совершает возвратно-поступательное движение.
2, 3, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
5, 7 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
3). А5, С5 – кинематические пары 5-го класса низшие, поступательные.
D5, N5, B5, M5, W5, E5, K5, S5 – кинематические пары 5-го класса низшие, вращательные.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 6,5; 2,1; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 2-й, т.к. наивысший класс группы Ассура входящий в состав механизма 2-й.
Задача 5.
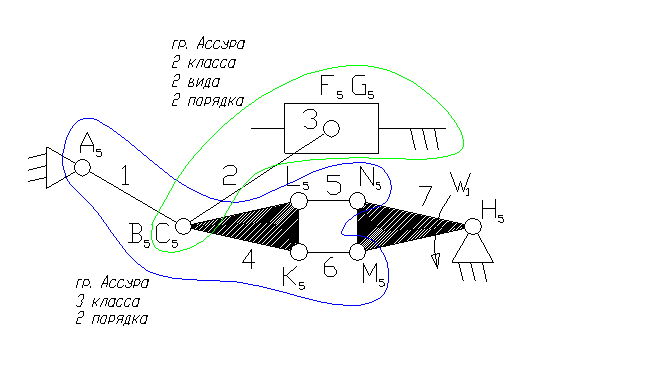7 – ведущее звено – кривошип.
1– коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 1,4,5,6. Осталось ведущее звено и стойка.
10). Группы Ассура 4-го класса нет.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 6.
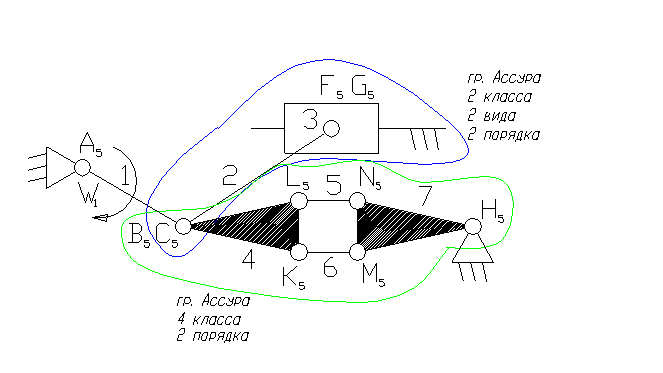
1– ведущее звено - коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
7 – кривошип.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
9). Группы Ассура 3-го класса нет.
10) Отсоединяем группу Ассура 4-го класса, состоящую из звеньев 4,5,6,7. Осталось ведущее звено и стойка.
11). Класс механизма 4-й, т.к. наивысший класс группы Асура, входящий в состав механизма 4-й.
Задача 7.
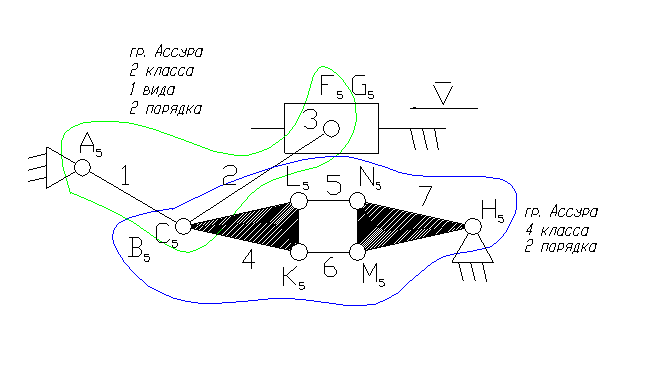
3- ведущее звено – ползун, совершает возвратно-поступательное движение.
1– коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 5, 6 – шатун – звено, которое совершает сложное плоско-параллельное движение.
7- кривошип.
3). A5, B5, C5, F5, K5, L5, N5, M5, H5 – кинематические пары 5-го класса низшие, вращательные.
G5 – кинематическая пара 5-го класса низшая, поступательная.
4). W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2.
9). Группы Ассура 3-го класса нет.
10). Отсоединяем группу Ассура 4-го класса, состоящую из звеньев 4,5,6,7. Осталось ведущее звено и стойка.
11). Класс механизма 4-й, т.к. наивысший класс группы Асура, входящий в состав механизма 4-й.
Задача 8.
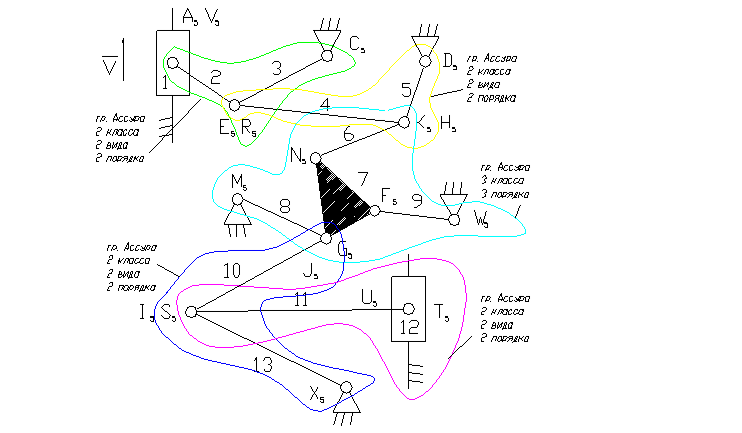1 – ведущее звено ползун,
12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается),
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематическая пара 5-го класса низшие, поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13; 11,12.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 4,5 и 2,3.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 9.
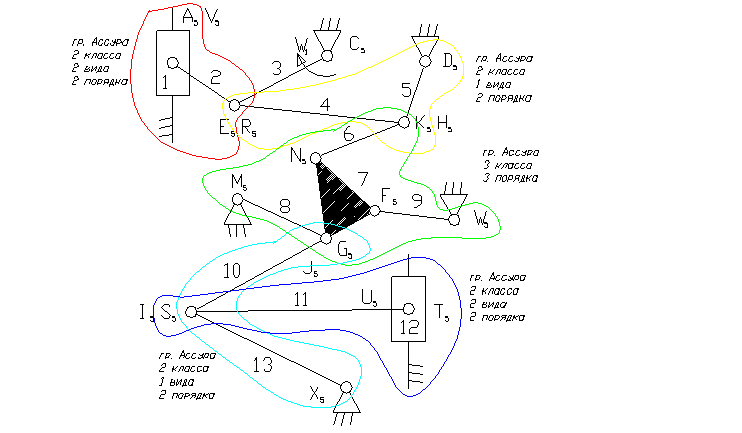
3 - ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3) A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4) W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5) Лишних степеней свободы нет.
6) Пассивных связей нет.
7) Высших кинематических пар нет.
8) Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13 и 11,12.
9) Отсоединяем группу Ассура 3-го класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 4,5 и 1,2.
Осталось ведущее звено и стойка.
11) Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 10.
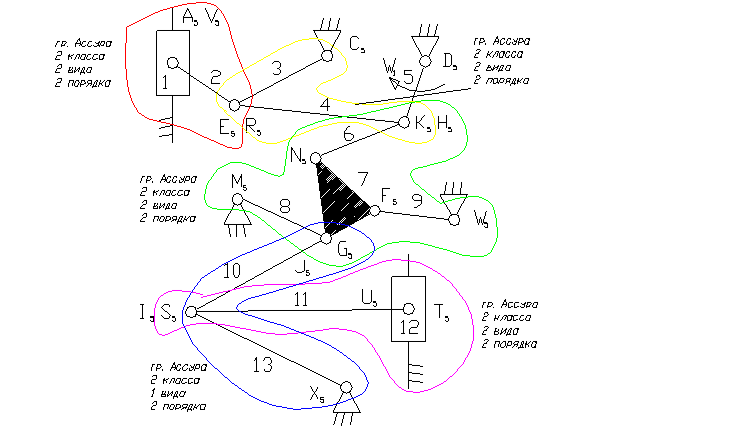
5 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3) A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4) W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5) Лишних степеней свободы нет.
6) Пассивных связей нет.
7) Высших кинематических пар нет.
8) Отсоединяем группу Ассура 2 класса, состоящую из звеньев 10,13 и 11,12.
9) Отсоединяем группу Ассура 3-го класса, состоящую из звеньев 6,7,8,9.
10). Отсоединяем группу Асура 2 класса, состоящую из звеньев 3,4 и 1,2.
Осталось ведущее звено и стойка.
11) Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 11.
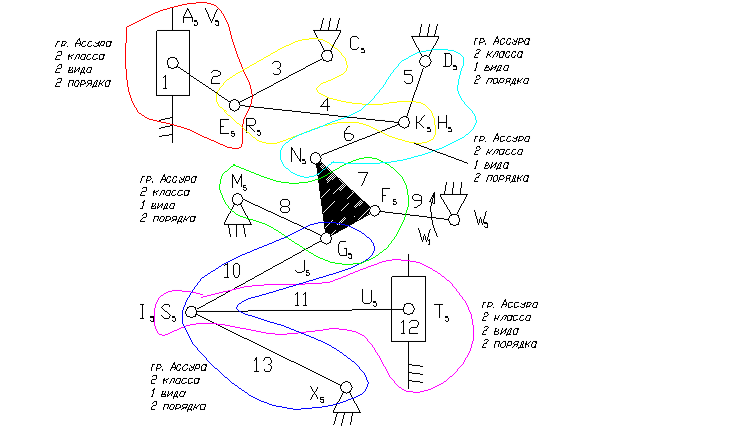
9 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие, поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 10,13; 11,12 и 7,8.
Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11) Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 12.
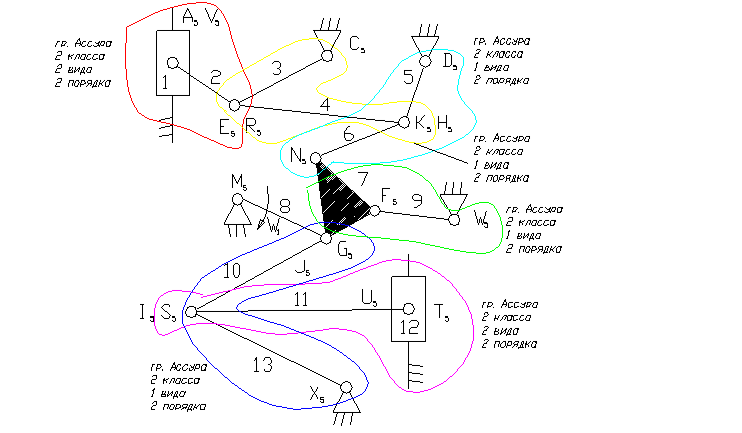
8 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 10,13; 11,12 и 7,9.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 13.
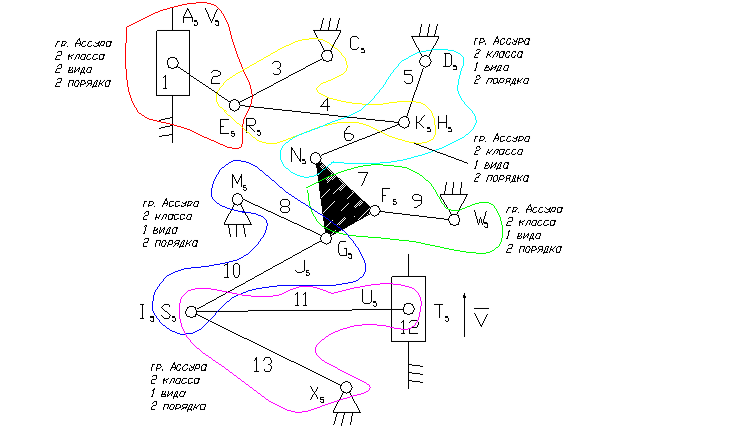12 – ведущее звено ползун.
1, – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 7,9; 8,10; 11,13.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 14.
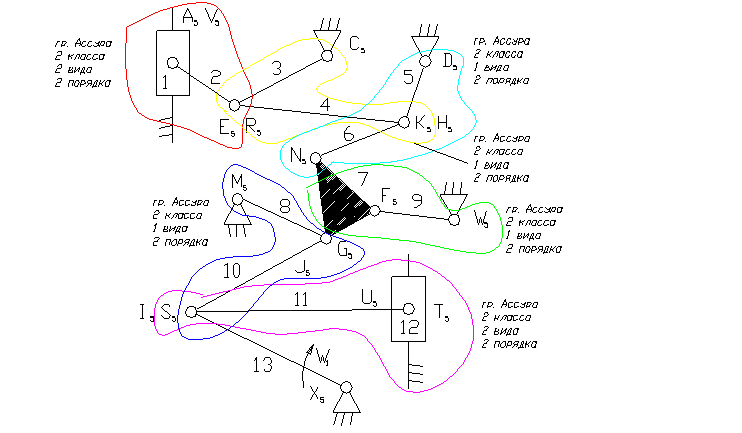
13 – ведущее звено коромысло.
1, 12 – ползун – звено, которое совершает возвратно-поступательное движение.
3, 5, 8, 9 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 11 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, D5, K5, H5, N5, M5, F5, W5, G5, J5, I5, S5, U5, X5 – кинематические пары 5-го класса низшие, вращательные.
V5, T5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 3,4; 5,6; 7,9; 8,10; 11,12.
Осталось ведущее звено и стойка.
9). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 15.
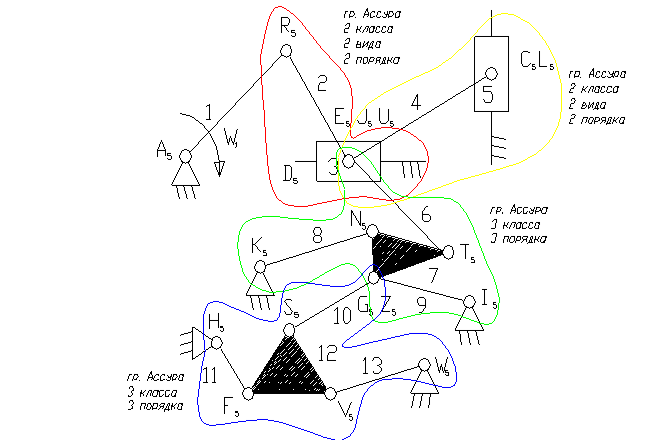
1 – ведущее звено кривошип – звено, которое совершает вращательное движение.
3, 5 – ползун.
8, 9, 11, 13 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 2,3.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 16.
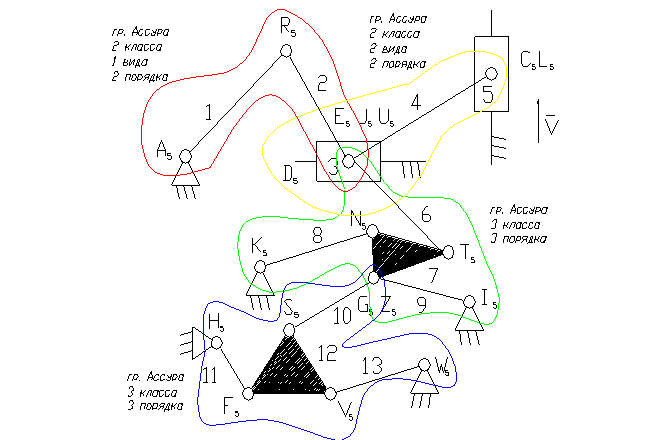
5 – ведущее звено ползун.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 3, 4.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 17.
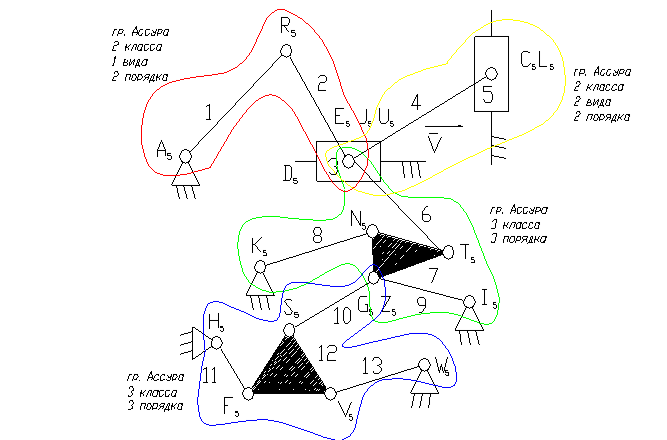3 – ведущее звено ползун.
5 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун .
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2 и 4,5.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
Осталось ведущее звено и стойка.
10). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 18.
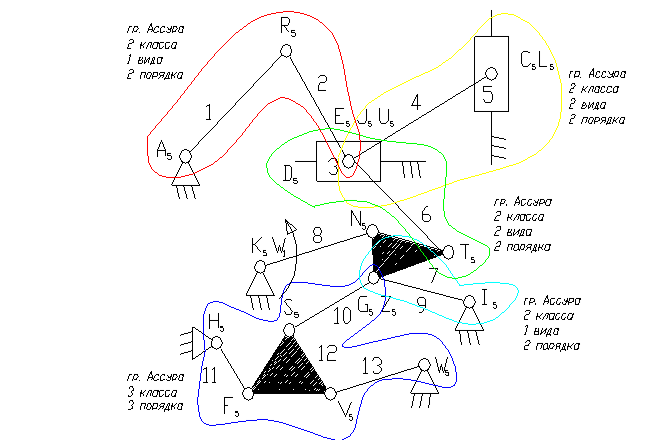8 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
9, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 7, 9.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 19.
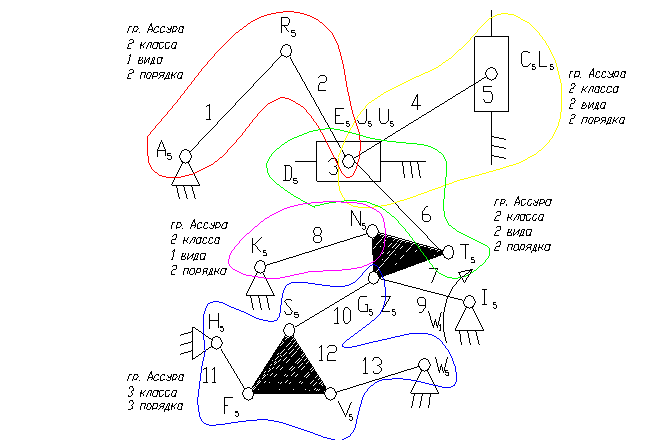9 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 11, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6.
9). Отсоединяем группу Ассура 3 класса, состоящую из звеньев 10,11,12,13 и 6,7,9,8.
10). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 7, 8.
Осталось ведущее звено и стойка.
11). Класс механизма 3-й, т.к. наивысший класс группы Асура, входящий в состав механизма 3-й.
Задача 20.
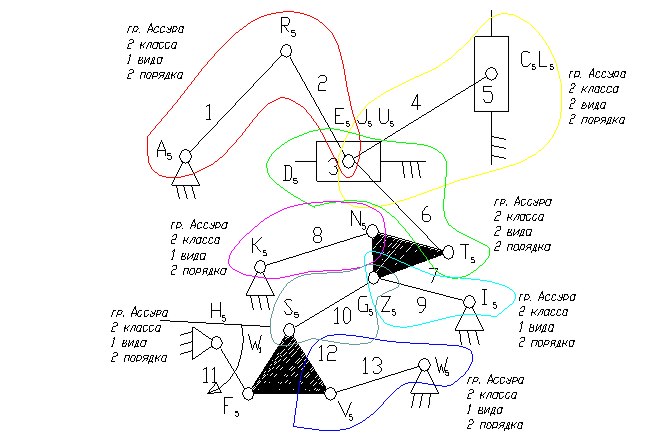
11 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 13 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6; 7,8; 9,10 и 12,13.
Осталось ведущее звено и стойка.
9). Класс механизма 2-ой, т.к. наивысший класс группы Асура, входящий в состав механизма 2-ой.
Задача 21.
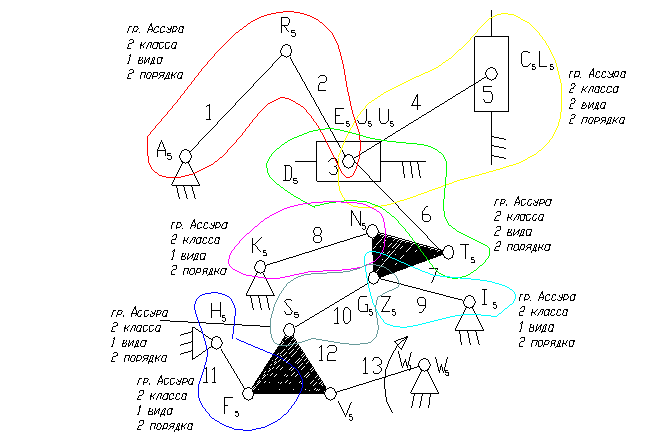
13 – ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1 – кривошип.
8, 9, 11 – коромысло.
2, 4, 6, 7, 10, 12 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, E5, R5, C5, K5, Z5, N5, F5, W5, G5, J5, I5, S5, V5, F5, , T5 – кинематические пары 5-го класса низшие, вращательные.
L5, U5 – кинематические пары 5-го класса низшие поступательные.
4). W = 3n - 2p5 - p4 = 3×13 - 2×19 = 1
5). Лишних степеней свободы нет.
6). Пассивных связей нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,6; 7,8; 9,10 и 11,12.
Осталось ведущее звено и стойка.
9). Класс механизма 2-ой, т.к. наивысший класс группы Асура, входящий в состав механизма 2-ой.
Задача 22.
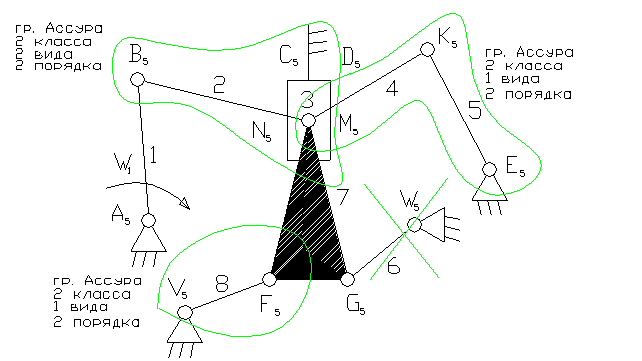1- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
5, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5; 7,8; 2,3. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 23.
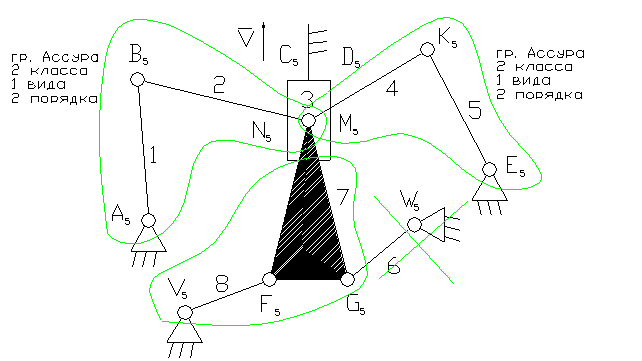
3- ведущее звено ползун.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 5, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 4,5; 7,8; 1,2. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 24.
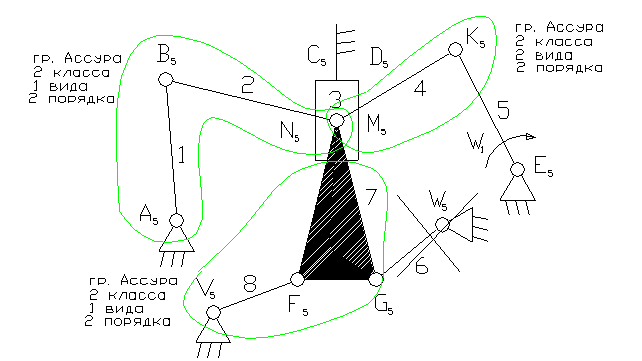
5- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 6, 8 – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 7,8; 3,4. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
Задача 25.
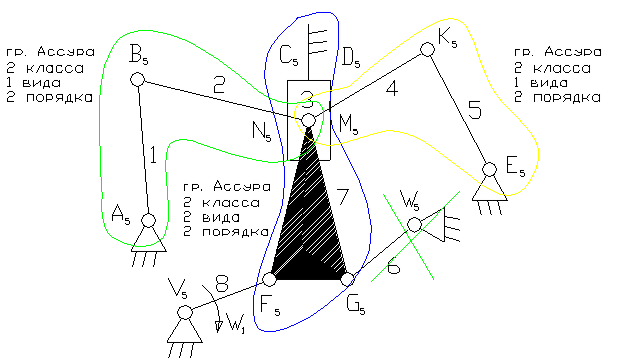
8- ведущее звено коромысло.
3 – ползун – звено, которое совершает возвратно-поступательное движение.
1, 5, 6, – коромысло – звено, которое совершает неполный оборот вокруг своей оси (качается).
2, 4, 7 – шатун – звено, которое совершает сложное плоско-параллельное движение.
3). A5, B5, C5, N5 , M5, K5, E5, V5, F5 , G5, , W5 – кинематические пары 5-го класса низшие, вращательные.
D5 – кинематическая пара 5-го класса низшая поступательная.
4). W = 3n - 2p5 - p4 = 3×8 - 2×12 = 0. На первый взгляд кажется, что это ферма. На самом деле звено 6 является пассивной связью и его можно удалить вместе с кинематическими парами: G5, , W5 .
5). Вновь определяем степень подвижности механизма, без звена 6, получаем: W = 3n - 2p5 - p4 = 3×7 - 2×10 = 1.
6). Лишних степеней свободы нет.
7). Высших кинематических пар нет.
8). Отсоединяем группу Ассура 2 класса, состоящую из звеньев 1,2; 4,5; 3,7. Осталось ведущее звено и стойка.
9). Группы Ассура 3-го класса нет
10). Группы Ассура 4-го класса нет
11). Класс механизма 2-й, т.к. наивысший класс группы Асура, входящий в состав механизма 2-й.
МЕХАНИЗМОВ
1. Цель И ЗАДАЧИ
Цель: изучить движение звеньев механизма без учета сил, вызывающих это движение.
ЗАДАЧИ
ОПРЕДЕЛЕНИЕ
ПЕРЕМЕЩЕНИЙ СКОРОСТЕЙ УСКОРЕНИЙ
S = ? V = ? a = ?
2. Масштабные коэффициенты
Действительная величина м м/с м/с2 Н Нм
m = ------------------------------------------------- = --- , ---- , ----, ---, ----.
Отрезок в мм на чертеже мм мм мм мм мм
ГОСТ 1-й ряд 2-й ряд
1 0,0001 …1000 2,5
2 0,0002… 4
5 0,0005…500
 |  |
3. Определение перемещений: S = ?
 |
Алгоритм: провести структурный анализ механизма, определить перемещения всех точек ведущего звена, а затем перемещения точек каждой группы Ассура, в порядке их присоединения к ведущему звену.
4. Определение скоростей : V = ?
Алгоритм:
 |
Шаг 1: провести структурный анализ
Шаг 2: определить скорости для ведущего звена механизма.
 |  |  |  |
|
|
 |
VA = 0, VB = VA + VBA = VBA ,
VB = w . LBA
Шаг 3: определить скорости для каждой группы Ассура в порядке их присоединения
 | |||
 | |||
VCB
C VC
VB
B
c
b
P,a
 |  | |
VC = VB + VCB
5. Определение ускорений : a = ?
Алгоритм:
 |
Шаг 1: провести структурный анализ механизма
Шаг 2: определить ускорения для ведущего звена
 |
П, a
| |  |  | |
aB = aA + aBA = aBA , aA = 0, b
n т
aBA = w2 . LAB , aBA = E . LAB , Е = 0, т.к. w = const.
Шаг 3: определить ускорения для каждой группы Ассура
т
a CB C a C
П, а
n
a CB
|
|
 |  | ||||
| | |||||
|
B
| ||||
| | ||||
a B
aC = aB + aCB ,
n т
aC = aB + aCB + aCB
6. Кинематические диаграммы.
6.1. Графическое дифференцирование
0 1 2 3 4 5 6 7 8 j
0v 0 1 2 3 4 5 6 7 8 j
HV
Алгоритм графического дифференцирования:
1. На 1-ом графике кривую линию на каждом участке заменяем прямой.
2. На 2-ом графике выбираем полюсное расстояние HV=20¸40 мм.
3. Прямую 01S с 1-го графика параллельно переносим в точку 0V
2-го графика до тех пор пока она не пересечёт ось V.
Отрезок отсекаемый на оси V показывает значение скорости на участке ( 01 ) 2-го графика.
4. Прямую 1S2S с 1-го графика параллельно переносим в точку 0V
2-го графика.
5. Аналогично поступаем на остальных участках.
6. Середины участков на 2-ом графике соединяем кривой линией.
j
0
1
2
3
4
5
6
7
6.2. Графическое интегрирование
8
A
0A 0 1 2 3 4 5 6 7 8
HA
V
 |
|
Алгоритм графического интегрирования:
1. На 1-ом графике кривую линию на каждом участке заменяем прямой.
2. На 1-ом графике выбираем полюсное расстояние Ha = 20¸40 мм.
3. Середину каждого участка на 1-ом графике параллельно сносим на ось A. Точку пересечения с осью A соединяем с точкой 0A.
4. Прямую 0A1A с 1-го графика параллельно переносим на участок 01 2- го графика.
5. На остальных участках поступаем аналогично.
7 . Вопросы для самопроверки.
1. Цель кинематического анализа механизма.
Ответ: изучить движение звеньев механизма без учёта сил, вызывающих это движение.
2. Как называются графики, построенные по полученным значениям кинематических величин?
Ответ: кинематические диаграммы.
3. Назовите численные значения масштаба.
Ответ: 1, 2, 2.5, 4, 5.
4. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек звеньев механизма в данный момент?
Ответ: план ускорений.
5. Единица измерения масштаба скорости?
Ответ: м сек-1 / мм.
6. Напишите формулу для определения численного значения нормальной составляющей ускорения любой точки кривошипа.
Ответ: аn = w2. R
7. Как определить направления угловой скорости звена?
Ответ: угловая скорость и вектор относительной скорости
направлены в одну сторону.
8. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки кривошипа.
Ответ:
9. Скорость самолета 2500 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 694,4 м/сек.
10. Скорость автомобиля 80 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 22 м.
11. Задачи КАМ.
Ответ: определение перемещений звеньев и траекторий, описываемых точками звеньев; определение скоростей отдельных точек звеньев и угловых скоростей звеньев; определение ускорений отдельных точек звеньев и угловых ускорений звеньев.
12. Понятие масштаба (масштабного коэффициента) в ТММ?
Ответ: Масштаб это отношение действительной величины к отрезку в мм, который изображает эту величину на чертеже.
13. Алгоритм графического интегрирования.
Ответ:
14. Напишите формулу для определения численного значения скорости любой точки кривошипа.
Ответ: V = w . R.
15. Чем задаётся положение ведущего звена, если оно входит в поступательную пару?
Ответ: функцией перемещения s = s(t).
16. Как определить направления углового ускорения звена?
Ответ: угловое ускорение направлено в сторону тангенциальной составляющей относительного ускорения.
17. С какой целью определяют ускорения точек звеньев механизма?
Ответ: например, для определения силы инерции.
18. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки кривошипа.
Ответ:
19. Скорость самолета 2400 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 666,7м/сек.
20. Скорость автомобиля 40 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 10 м.
21. Цель кинематического анализа механизма.
Ответ: изучить движение звеньев механизма без учёта сил, вызывающих это движение.
22. Алгоритм графического дифференцирования.
Ответ:
23. Для каких целей строят кинематические диаграммы?
Ответ: для кинематического исследования механизма.
24. Единица измерения масштаба времени?
Ответ: сек / мм
25. Чем определяется положение ведущего звена, если оно входит во вращательную пару, со стойкой?
Ответ: функцией угла поворота j = j(t).
26. С какой целью определяют перемещения (траектории) точек звеньев механизма?
Ответ: для построения кинематических диаграмм, а также для выбора размеров корпусных деталей при проектировании механизма.
27. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки ползуна.
| |  | |  |
Ответ: VB = VA + VBA = VA
28. Скорость самолета 2300 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ: 638,9 м/сек.
29. Напишите формулу для определения угловой скорости w (рад./сек), если известна частота вращения n (об./мин.).
Ответ: w = 2 . П . n / 60
30. Скорость автомобиля 90 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ: 25 м.
31. Задачи КАМ.
Ответ:
32. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
Ответ:
33. Единица измерения масштаба длины?
Ответ: м / мм.
34. Напишите формулу для определения численного значения тангенциальной составляющей ускорения любой точки кривошипа.
Ответ: аt = Е .R.
35. С какой целью определяют скорости точек звеньев механизма?
Ответ: например, для выбора типа смазки.
36. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки ползуна.
Ответ:
37. Напишите формулу для определения угловой скорости звена, если известна частота вращения.(об./мин.).
Ответ:
38. Скорость самолета 2200 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
39. Скорость автомобиля 50 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
40. Скорость пули 200 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ: 720 км.
41. Цель кинематического анализа механизма.
Ответ:
42. Единица измерения масштаба угла поворота?
Ответ: град. / мм, или рад./мм.
43. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки шатуна.
Ответ:
44. Скорость самолета 2000 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
45. Скорость автомобиля 60 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
46. Скорость пули 220 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
47. Спортсмен пробегает 100 метров за 10 сек. А сколько километров спортсмен мог бы пробежать за один час, если бы двигался с такой же скоростью?
Ответ: 36 км.
48. Что такое кинематические диаграммы.
Ответ: графики, построенные по полученным значениям кинематических величин.
49. Что такое план скоростей?
Ответ: чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
50. Что такое план ускорений.
Ответ: чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек звеньев механизма в данный момент?
51. Задачи КАМ.
Ответ:
52. Как называются графики, построенные по полученным значениям кинематических величин?
Ответ:
53. Понятие масштаба в ТММ?
Ответ:
54. Что такое графическое дифференцирование?
Ответ:
55. Как называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент?
Ответ:
56. Единица измерения масштаба угла поворота?
Ответ:
57. Сделайте чертеж и напишите векторное уравнение для определения ускорения любой точки шатуна.
Ответ:
57. Скорость самолета 1800 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
58. Скорость автомобиля 70 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
59. Скорость пули 240 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
60. Цель кинематического анализа механизма.
Ответ:
61. Кратный каким числам выбирается масштаб?
Ответ:
62. Для каких целей строят кинематические диаграммы?
Ответ:
63. Сделайте чертеж и напишите векторное уравнение для определения скорости любой точки шатуна.
Ответ:
64. Скорость самолета 1700 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
65. Скорость автомобиля 100 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
66. Скорость пули 260 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
Ответ:
67. Спортсмен пробегает 100 метров за 11 сек. А сколько километров спортсмен мог бы пробежать за один час, если бы двигался с такой же скоростью?
Ответ:
68. Скорость самолета 1400 км/час. А сколько метров самолет пролетает за одну секунду?
Ответ:
69. Скорость автомобиля 120 км/час. Какой путь автомобиль пройдет за одну секунду?
Ответ:
70. Скорость пули 300 м/сек. Сколько километров пуля пролетит за один час, если пренебречь сопротивлением воздуха и притяжением Земли?
8. Задачи для самостоятельного решения.
1. Построить план скоростей и ускорений для заданных механизмов, считая, что ведущее звено задано (выбрать ведущее звено самостоятельно). Размеры звеньев известны.
Задача № 1.1.
Задача № 1.2.
Задача № 1.3.
 | |||
 | |||
Задача № 1.4.
Задача № 1.5.
2. Построить механизм в заданном положении.
2.1. Построить положение шарнирного четырёхзвенника при j1=300, если lАВ=30 мм, lВС=lAD=80 мм, lCD=70мм.
2.2. Построить положение кривошипно-ползунного механизма, если j1=450,
lAB=50мм, lВС=150мм.
2.3. Построить положение кривошипного механизма с качающимся ползуном при j1=900, если lAB=40 мм, lAC=120 мм.
К задаче 2.1. К задаче 2.2. К задаче 2.3.
3. Определить численные значения скоростей и ускорений с помощью построения планов скоростей и ускорений.
3.1. Найти абсолютные скорость и ускорение точки Е и угловые скорость и ускорение звена CD (звена 3) четырёхзвенного четырёхшарнирного механизма. Дано: lAB = 30мм, lBC = lCD = lAD = 60мм, lBE = lCE = 35мм, j = 300, угловая скорость кривошипа AB (звена l) постоянна и равна w1 = 20 сек-1.
3.2. Найти угловые скорость и ускорение звена BC (звена 2) кривошипно-ползунного механизма. Дано lAB = 60мм, lBC = 180 мм, j1 = 1200, угловая скорость кривошипа АВ постоянна и равна w1=100 сек-1.
К задаче 3.1. К задаче 3.2.
3.3. У механизма двигателя внутреннего сгорания с прицепным шатуном найти:
абсолютные скорость и ускорение поршня 5 (скорость и ускорение точки Е). Дано: lАВ = 0,06м , lВС = lDE = 0,180м , lВD = 0.06м , Ð DBC =b=600, d = 60°, угловая скорость кривошипа АВ постоянна и равна w1=200 сек-1, j1=450.
3.4. Найти скорость vC точки С механизма Робертса. Дано: lBC= lCE= lCD= lDG=
lEF=50мм, lDЕ=24мм, Н = 10 мм, Н1 =25мм, Н2 = 50мм, угловая скорость звена АВ равна w1=5 сек-1, j1=2400.
К задаче 3.3. К задаче 
3.4.
3.5. Для заданного положения четырехзвенного четырехшарнирного механизма определить угловые скорости и ускорения всех его звеньев и скорость и ускорение точки С. Дано: w1=20 сек-1, lАВ = 100мм , lBC= lCD=400мм, отрезки АВ и ВС располагаются на одной прямой, а угол ВСD =900.
3.6. Для заданного положения четырехзвенного четырехшарнирного механизма найти угловые скорости и ускорения всех звеньев и скорость и ускорение точки С. Дано: угловая скорость кривошипа АВ постоянна и равна w1=20 сек-1, lАВ = 100мм , lАВ = 100мм , lBC= lCD=400мм, Ð АВС =Ð DBC = 900.
3.7. Для заданного положения кривошипно-ползунного механизма найти скорость и ускорение точки D звена 2 и угловые скорости и ускорения всех звеньев. Дано:угловая скорость кривошипа АВ постоянна и равна w1=80 сек-1
К задаче 3.5. К задаче 3.6. К задаче 3.7.
Вопросы для самопроверки.
1. Что такое тахограмма механизма?
2. Время работы механизма?
3. Коэффициент неравномерности хода механизма?
4. Кинетическая энергия механизма?
5. Что такое приведенная масса механизма?
6. Что такое приведенная сила механизма?
7. Диаграмма Виттенбауэра?
8. Что можно определить по диаграмме Виттенбауэра?
9. Что такое вибрации механизма?
10. Задачи для самостоятельного решения.
1. Для кривошипно-ползунного механизма определить приведённый к валу 1 звена АВ момент МП от силы Р3 =1000н, приложенной к ползуну 3, и приведённый к тому же валу момент инерции IП от массы ползуна 3, если масса ползуна м3= 4кг, lAB=100мм, lBС=400мм, j1 =90°.
2.
 |  |
Для четырёхзвенного шарнирного механизма определить приведённый к валу 1 звена АВ момент МП от момента М3 =40 нм, приложенного к коромыслу 3, и приведённый момент инерции IП от массы коромысла, если момент инерции коромысла относительно оси D равен ID =0,016 кгм2, lAB=100мм, lBС=lСD=400мм, углы j1 =j2 =j3 =90°.
К задаче 1 К задаче 2
3. Для кривошипного механизма с качающимся ползуном определить приведённый к валу 1 звена АВ момент МП от момента М3 =4 нм, приложенного к ползуну 3, если его момент инерции относительно оси С равен IC =0,004 кгм2, lAB=100мм, lAС=300мм, j1 =180°.
 |
К задаче 3
4. Для кривошипно-ползунного механизма определить приведённый к валу 1 звена АВ момент инерции IП от массы шатуна ВС, если его масса м2=0,2 кг, центральный момент инерции IS2=0,0032 кгм2, центр масс S2 делит расстояние ВС пополам, lAB=50мм, lВС=400мм. Рассмотреть случаи : а) j1 =0°, в) ) j1 =90°.
Заходы червяка
 |
Многоступенчатые редуктора
1
2 3
4 5 6
Ступени
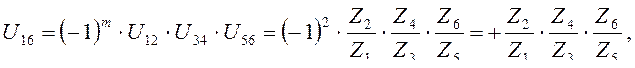
где m – число внешних зацеплении.
 |
4. Рядовое соединение зубчатых колёс с промежуточными (паразитными) колёсами
1
2
3
4
4
Планетарные редуктора
2 3 4
 |  |
1 H
1 – подвижное колесо,
2 и 3 – блок сателлитов (два колеса жестко закрепленных
на одном валу),
4 – неподвижное колесо,
Н – водило (вращающееся звено, которое соединяется с
осью сателлитов).
Алгоритм определения передаточного отношения от
колеса 1 к водилу H при неподвижном колесе 4: U 1 H (4) = ?
1. Мысленно остановить водило и определить передаточное отношение от подвижного колеса к тому колесу, которое в планетарном механизме было неподвижным:
Z2 . Z4 Z2 . Z4
U14(H) = (-1)m . U12 . U34 = (-1)1 . =
Z1 . Z 3 Z 1 . Z 3
2 3 4
 | |||||||
 | | ||||||
 | |||||||
1
| |  |
2. Полученный результат вычесть из 1:
Z 2 . Z 4 Z 2 . Z 4
U 1 H (4) = 1 ( ) = 1 +
Z 1 . Z 3 Z 1 . Z 3
 |
6. Пример определения передаточного отношения планетарного редуктора с одним внешним и одним внутренним зацеплением.
1.
 |
Мысленно останавливаем водило и определяем передаточное отношение от подвижного колеса 1 к тому колесу, которое было неподвижным 4:
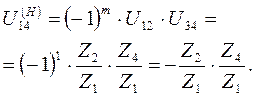
2. Полученный результат вычитаем из 1:
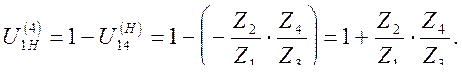
Вопросы для самопроверки
1.Что означает знак ( – ) в передаточном отношении?
Ответ: угловые скорости входного и выходного звена направлены в противоположные стороны.
2. Как определить число заходов червяка?
Ответ: посмотреть в торец червяка и подсчитать количество ниток.
3. На какие виды передач классифицируются механические передачи?
Ответ: с гибкими звеньями; фрикционные; зубчатые.
4. У каких зубчатых передач требуется определить знак передаточного отношения?
Ответ: у зубчатых передач относящихся к плоским механизмам.
5. Сколько заходов может быть у червяка?
Ответ: от 1 до 4 заходов.
6. Из скольких звеньев состоит одноступенчатый редуктор?
Ответ: из трех.
7. Чему равна степень подвижности планетарного редуктора?
Ответ: 1.
8. Чему равна степень подвижности дифференциального редуктора?
Ответ: 2 и больше.
9. По какому принципу классифицируются зубчатые механизмы?
Ответ: оси параллельны; пересекаются; скрещиваются.
10. Какие зубья бывают у зубчатых колес с параллельными осями?
Ответ: прямые; косые; шевронные.
11. Какое звено в червячной передаче является ведомым?
Ответ: зубчатое колесо.
12. Какое звено в червячной передаче является ведущим?
Ответ: червяк.
13. Назовите виды гибких звеньев.
Ответ: ремень; цепь.
14. К какому типу механизмов относится червячная передача?
Ответ: пространственный.
15. На что влияют промежуточные (паразитные) колеса в рядовом соединении зубчатых колес?
Ответ: на знак передаточного отношения.
16. На что не влияют промежуточные (паразитные) колеса в рядовом соединении зубчатых колес?
Ответ: на величину передаточного отношения.
17. Что означает число 0,1 в передаточном отношении зубчатой передачи?
Ответ: частота вращения выходного колеса в 10 раз больше частоты входного.
18. Что означает число 0,2 в передаточном отношении зубчатой передачи?
Ответ: частота вращения выходного колеса в 20 раз больше частоты входного.
19. Что означает число 2 в передаточном отношении зубчатой передачи?
Ответ: частота вращения выходного колеса в 2 раз меньше частоты входного.
20. Что означает число 10 в передаточном отношении зубчатой передачи?
Ответ: частота вращения выходного колеса в 10 раз меньше частоты входного, а число зубьев выходного колеса в 10 раз больше числа зубьев входного.
8. Задачи для самостоятельного решения.
Определить передаточное отношение в редукторах, если известно число зубьев зубчатых колес.
Задача № 1 
. 
2 6
 | |||
| | |||
4
 | |  |
H
 |  |
1 3 5
Задача № 2.
 |  |
1 3 4
5 6
 |  |  | |||||
| | |||||||
2 Н
 |  |
Задача № 3.
2 3 4
5
 | |||||||
 |  | | |||||
6
6
1
 | |
7
Задача № 4.
1 4 5 6
2 3 Н
Задача № 5.
 |  |
2 3 4 6 7
 | |
1 Н1 5 Н2 8
Задача № 6.
 | |||
 | |||
1 Червяк Червячное
колесо
2
 | |||||
| | | ||||
3 4
Задача № 7.
Z1=40; Z2=10; Z3=60; Z4=20; Z5=40; Z6=10; Z7=50; Z8=30; ZЧ=3; ZK=60;
n1=3000 об./мин.; nK=?
 | |||||||||
 | | | | ||||||
Z1
ZK
Z2
Z5
Z7
Z4 Z6 Z8
ZЧ
Z3
Задача № 8.
Z1=10; Z2=20; Z3=5; Z4=50; Z5=30; Z6=15; Z7=90;
U1 H=? UH 1=?
Z7
Z6
H
Z3
Z5
Z2
Z4
Z1
 |
Задачи № 9,10,11.
 |
9. Примеры решения задач.
9.1.Определение передаточного отношения планетарного редуктора с двумя внешними зацеплениями.
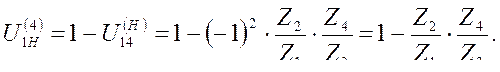
9.2. Определение передаточного отношения сложного многоступенчатого редуктора.
16
7 8 11 12
1 15 17
H1 9 H2
2 5 10 14 18
13
3 4
6
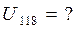
Решение:
1. Многоступенчатый механизм разбиваем на отдельные ступени и находим передаточные отношения для каждой ступени.
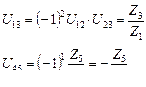
2. Для двух планетарных механизмов передаточные отношения находим отдельно для каждого механизма по формуле Виллиса:
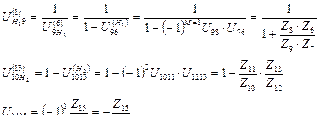
3. Полученные значения передаточных отношений перемножаем:
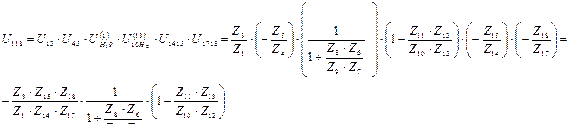
МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОУ ВПО Иркутский Государственный Технический Университет
ФТиКМ
Кафедра
Конструирования и стандартизации в машиностроении
П.В. Королев канд.техн.наук., доцент
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Конспект лекций
По дистанционному обучению
Иркутск 2010
Теория механизмов и машин. Конспект лекций по дистанционному обучению для студентов механических специальностей дневной, вечерней и заочной формы обучения высших технических учебных заведений. Составил: канд. техн. наук., доцент
П.В. Королев. – Иркутск, 2010. – …… с.
Представлен конспект лекций по предмету «Теория машин и механизмов». В конспекте отражены наименования тем, приведены рисунки, схемы, формулы и основные определения. Конспект лекций представляет собой методический материал для дистанционного обучения, который позволяет студенту:
- сократить время, затрачиваемое на выполнение чертежей, схем и написание формул,
- подробнее конспектировать материал лекции,
- изучать новый материал, «следить за мыслью лектора»,
- знать наименование будущих тем лекций и планировать свою подготовку к ним.
Для закрепления в памяти пройденного материала в конце каждой темы приведены вопросы для самопроверки с ответами и задачи для самостоятельного решения, подобные тем, которые встречаются на экзамене или зачете.
Конспект лекций по ТММ предназначен для студентов специальностей: АТ, СДМ, АС, ММ, СП, ЭЛ, СМ, ГМ, БТП, БЖТ дневной, вечерней и заочной формы обучения при изучении ими теоретической части курса и выполнении курсового проекта по теории механизмов и машин.
ОГЛАВЛЕНИЕ
ТЕМА 1: СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ……………
1. История развития ТММ.………………………………..
2. Вопросы, которые изучает ТММ ………………………
3. Основные понятия ТММ, термины и определения …..
4. Классификация кинематических пар ………………….
5. Степень подвижности плоских и пространственных
механизмов……………………………………………
6. Пассивные связи. Лишние степени свободы………..
7. Замена высших кинематических пар низшими……..
8. Принцип образования плоских механизмов…………
9. Классификация групп Ассура………………………...
10. Алгоритм проведения структурного анализа………..
11. Вопросы для самопроверки…………………………...
12. Задачи для самостоятельного решения………………
13. Примеры решения задач………………………………
ТЕМА 2: КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ…….
1. Цель и задачи кинематического анализа……………..
2. Масштабы в ТММ……………………………………...
3. Определение перемещений……………………………
4. Определение скоростей………………………………..
5. Определение ускорений……………………………….
6. Кинематические диаграммы…………………………..
7. Вопросы для самопроверки……………………………
8. Задачи для самостоятельного решения……………….
9. Примеры решения задач……………………………….
ТЕМА 3,4: ДИНАМИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА………..
1. Цель и задачи динамического анализа………………
ТЕМА 3: СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА……………………
1. Классификация сил в механизме…..…………………
2. Методы силового расчета механизма………………..
3. Порядок кинетостатического расчета механизма…..
4. Реакции в кинематических парах механизма……….
5. Порядок силового расчета группы Ассура………….
6. Порядок силового расчета ведущего звена…………
7. Теорема о жестком рычаге Жуковского…………….
8. Статическое уравновешивание вращающихся масс..
9. Вопросы для самопроверки…………………………..
10. Задачи для самостоятельного решения………………
11. Примеры решения задач………………………………
ТЕМА 4: ДИНАМИКА МЕХАНИЗМА…………………………….
1. Тахограмма механизма………………………………..
2. Коэффициент неравномерности хода механизма……
3. Кинетическая энергия механизма…………………….
4. Приведенная масса (приведенный момент
инерции) механизма………………………
5. Приведенная сила (приведенный момент)……………
6. Диаграмма Фердинанда Виттенбауэра……………….
7. Определение момента инерции маховика……………
8. Вопросы для самопроверки……………………………
9. Задачи для самостоятельного решения……………….
10. Примеры решения задач……………………………….
ТЕМА 5: МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ………………………….
1. Классификация механизмов передач…………………
2. Классификация зубчатых механизмов……………….
3. Многоступенчатые редуктора………………………...
4. Рядовое соединение зубчатых колес с (промежуточными)
паразитными колесами….. ……………………
5. Планетарные редуктора……………………………….
6. Вопросы для самопроверки…………………………..
7. Задачи для самостоятельного решения………………
8. Примеры решения задач………………………………
ТЕМА 6: ЭВОЛЬВЕНТНОЕ ЗАЦЕПЛЕНИЕ………………………
1. Основная теорема зацепления……………………….
2. Требования, предъявляемые к профилям зубьев
зубчатых колес: кинематические, динамические,
технологические, эксплуатационные…….…
3. Основные размеры нулевых зубчатых колес……….
4. Эвольвента окружности……………………………...
5. Ненулевые зубчатые колеса:
положительные и отрицательные……………
6. Методы выбора коэффициентов смещения
инструментальной рейки ……………
7. Коэффициент перекрытия (качественный
показатель зацепления)…………………
8. Таблица инволют……………………………………
9. Вопросы для самопроверки………………………..
10. Примеры решения задач……………………………
ТЕМА 7: КУЛАЧКОВЫЕ МЕХАНИЗМЫ……………………….
1. Особенности кулачковых механизмов…………….
2. Классификация кулачковых механизмов…………
3. Анализ кулачковых механизмов…………………..
4. Мягкие и жесткие удары…………………………...
5. Углы давления в кулачковых механизмах………..
6. Синтез кулачковых механизмов…………………..
7. Вопросы для самопроверки………………………..
8. Задачи для самостоятельного решения……………
9. Примеры решения задач……………………………
Контрольные вопросы к зачету и экзамену по курсу ТММ ………..
Список рекомендованной литературы……………………………………
Пример выполнения курсовой работы по ТММ………………………..
ТЕМА 1: СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ
История развития ТММ.
Леонардо Да Винчи (1452 – 1519 г.)
| |
Леонард Эйлер (1707 – 1783 г.) Эвольвента
Чебышев Пафнутий Львович (1821 – 1894 г.)
W = 3n – 2p5 – p4
Сомов П.О. (1852- 1919 г.) и Малышев А.П. (1879-1962 г.)
W = 6n – 5p5 – 4p4 – 3p3 – 2p2 – p1
Р. Виллис (1800 – 1875 г.)
(j) (H)
U iH = 1 – U ij
i –подвижное колесо, j – неподвижное колесо, Н - водило
Ассур Леонид Владимирович (1878 – 1920 г.) – принцип образования плоских механизмов.
Леонардо да Винчи (1452 – 1519 г.): научное изучение рукописей началось более трех столетий спустя после смерти Леонардо, так как многое из того, что они заключали, не могло быть понято его современниками (шариковый подшипник, артиллерийские снаряды со стабилизатором, многоствольная скорострельная пушка и многое другое).
Эйлер Леонард (1707 – 1783 г.): в 1736 г. вышел его трактат по механике, принесший ему мировую славу. Выходят в свет его книги: «Интегральное исчисление», «Элементы алгебры», «Новая теория движения Луны», «Морская наука» и др. После себя Л. Эйлер оставил более 850 научных работ.
Ползунов Иван Иванович (1730-1766 г.): построил лесопильную мельницу, в которой подъем бревен и их подача были механизированы, сконструировал сооружения для подъема сплавных судов. В 1765 году было проведено успешное испытание паровой машины созданной Ползуновым, которая впервые в мире имела два цилиндра и рабочий вал. На создание паровой машины Екатерина 11 выделила 400 рублей, а доход, который приносила эта машина заводу составлял 440 рублей в сутки !
Кулибин Иван Петрович (1735-1818 г.): часовщик-изобретатель, создатель телескопов, первого в мире ахроматического микроскопа, электрических машин, термометра, оптического телеграфа, самодвижущаяся коляска (1791 г.), водоходное судно. Разработал теорию моделирования и расчета арочных мостов.
Чебышев Пафнутий Львович (1821 – 1894 г.): гениальный математик и механик. Сконструировал: оригинальные паровые машины, арифмометр, центробежный регулятор, самокатное кресло, лодку с гребным механизмом, стопоходящую машину и др. В работе «О параллелограммах» (1869 г.) Чебышев П.Л вывел структурную формулу плоского механизма:
W = 3 n – 2 p5 – p4.
Сомов Павел Осипович (1852-1919 г.): вывел структурную формулу пространственного механизма:
W = 6 n – 5 p5 – 4 p4 – 3 p3 – 2 p2 – p1 .
Жуковский Николай Егорович (1847-1921 г.): профессор Московского университета и Московского технического училища. Научные интересы Жуковского Н.Е. были многогранны: от аэромеханики (аэродинамика) и гидромеханики до исследования хвостов комет, общей теории устойчивости движения, теории регулирования машин, прочности велосипедного колеса, теории ветряных двигателей и др.
Леонид Владимирович Ассур (1878-1920 г.): профессор Петербургского политехнического института открыл закон образования плоских механизмов.
Артоболевский Иван Иванович, Колчин Н. И., Мовнин М. С., Кожевников С.Н.
Вопросы, которые изучает наука «ТММ».
ТММ
Строение Кинематика Динамика
механизма механизма механизма
| |
Даны Найти Дан Найти
свойства. механизм. механизм. свойства.
Синтез Анализ
3. Основные понятия ТММ, термины и определения.
| |
Машина – это устройство, предназначенного для преобразования:
- энергии (двигатель внутреннего сгорания, турбина ),
- информации (ЭВМ),
- материалов (токарный станок, пилорама, пресс, кран).
Каждая машина состоит чаще всего из нескольких механизмов.
Механизм- это система тел, предназначенных для преобразования одного вида движения в другой вид движения, например: вращательное во вращательное, вращательное в возвратно-поступательное и т.д.
Механизм состоит из звеньев:
- стойка – неподвижное звено любого механизма,
- кривошип – совершает вращательное движение,
- шатун – совершает сложное плоско-параллельное движение,
- ползун – совершает возвратно-поступательное движение,
- коромысло (качающееся звено) – совершает неполный оборот вокруг оси,
- кулиса – звено, совершающее поступательное, вращательное или качательное движения, по которому перемещается ползун. В этом случае ползун называют камень кулисы.
Звенья в механизме соединяются между собой подвижным соединением. Подвижное соединение двух звеньев называется кинематической парой.
Если соединяются два звена, то будет одна кинематическая пара. Если соединяются три звена, то будет две кинематических пары. Если соединяются N звеньев, то будет N-1 кинематическая пара.
4. Классификация кинематических пар.
Кинематические пары
| | |
Классы Группы
(Смотри с……)
Звено Звено
Подвижное
соединение
Класс кинематической пары = S (числу ограничений).
Z
H = 6
S = 0
S - число ограничений
H – степень свободы
S = 6 - H
X Y
| |
1. Шар – плоскость: H = 5; S = 1; класс 1.
2. Шар – цилиндр: H = 4; S = 2; класс 2.
| |
| |
3. Сферическая: H = 3; S = 3; класс 3.
| |
| |
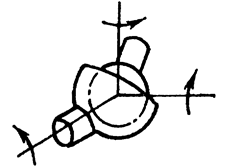4. Плоскостная: H = 3; S = 3; класс 3.
5.Цилиндрическая: H = 2; S = 4; класс 4.
| |
| |
6. Сферическая с пальцем: H = 2; S = 4; класс 4.
| |
| |
7.Поступательная: H = 1; S = 5; класс 5.
| |
| |
| |
8.Вращательная: H = 1; S = 5; класс 5.
| |
| |
9.Винтовая: H = 1; S = 5; класс 5.
| |
Группы кинематических пар
Высшие кинематические пары – контакт между звеньями происходит по линии или в точке.
Низшие кинематические пары - контакт между звеньями происходит по поверхности.
Дата: 2019-03-05, просмотров: 308.
