Перейдем к определению коэффициентов модели многофакторной регрессии, в предположении, что для нее выполняются предпосылки (1)-(4).

Неизвестные параметры модели будем искать с помощью 1МНК (одношагового метода наименьших квадратов), суть которого, как уже отмечалось, состоит в определении такого набора параметров модели b, при котором сумма квадратов остатков (ESS) будет минимальной. Из уравнения (4.3) имеем:

u=Y-X b                                               (4.9)

Тогда

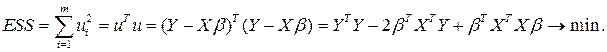
(4.10)

    Необходимое условие экстремума – равенство нулю частных производных выражения (4.10) в матричной форме можно записать так:

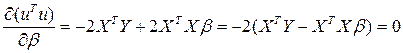                  (4.11)

Отсюда последовательно получаем:

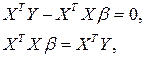
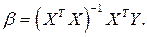                             (4.12)

Необходимо отметить, что классическая линейная многофакторная модель (4.2), (4.3) – это теоретическая модель, которая должна соответствовать всей генеральной совокупности. Однако, в реальных исследованиях, это уравнение строится на основе выборочных данных и при вычислении параметров модели по формуле (4.7) можно говорить лишь о их вероятностных (случайных) значениях 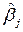, полученных на основе эмпирических данных:

.                               (4.13)

Необходимо отметить, что оценки параметров модели в соответствии с методом 1МНК являются достаточно чувствительными к точности расчетов и адекватности аналитической формы модели.

Для вычисления вектора 1МНК – оценок 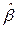 по формуле (4.13) применяют следующий порядок расчетов:

· найти матрицу 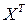, транспонированную к матрице регрессоров Х;

· вычислить произведение матриц ;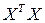

· умножить транспонированную матрицу регрессоров на вектор регрессандов Y, т.е. найти вектор ;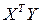

· найти матрицу 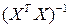, обратную к ;

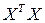· рассчитать вектор 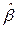 как произведение этой обратной матрицы и вектора .

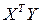Подставляя компоненты вектора 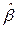, определенные по формуле (4.8), в оцениваемое регрессионное уравнение, получаем оцененную с помощью 1МНК эмпирическую регрессионную функцию

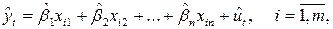                       (4.14)

где 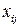 – значение регрессора  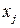в наблюдении i ( ),

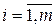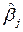     – оценки параметров классической модели ( )

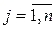Величина 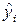 является прогнозируемой (условной) величиной математического ожидания регрессанта (значением систематической части регрессанта), которая вычисляется на основании эмпирической функции регрессии по конкретным значениям регрессионных коэффициентов  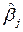и соответствующим значениям регрессоров , .

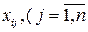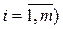Эмпирические коэффициенты 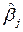 имеют конкретную экономическую интерпретацию: изменение величины 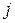-го регрессора на единицу при прочих равных условиях (ceteris paribus) вызывает изменение оцениваемой величины  единиц.

В MS Excel получить коэффициенты линейной многофакторной модели можно с помощью инструмента "Анализ данных / Регрессия"

[1] Стохастическая означает вероятностная. Связи между случайными явлениями называют вероятностными, или стохастическими связями. Этот термин подчеркивает их отличие от детерминированных или функциональных связей в математике.В функциональных связях каждому значению первого признака всегда соответствует (в идеальных условиях) совершенно определенное значение другого признака. В корреляционных связях каждому значению одного признака может соответствовать определенное распределение значений другого, признака, но не определенное его значение.