Тема 4. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Тема 4. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ

1. Обоснование задачи исследования согласованных действий. 1

2. Коэффициент корреляции Пирсона. 4

3. Регрессионный анализ 6

3.1. Спецификация простой регрессионной модели. 8

3.2. Оценка параметров линейной регрессионной модели. 12

3.3. Многофакторная линейная регрессия. 17

3.4. Оценка параметров линейной многофакторной модели. 18

Коэффициент корреляции Пирсона

Формула расчета коэффициента корреляции построена таким образом, что, если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреляции Пирсона. Если же связь между переменными Х и У не линейна, то Пирсон предложил для оценки тесноты этой связи так называемое корреляционное Отношение

Коэффициент корреляции рассчитаем по формуле:

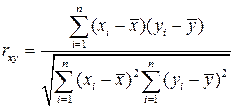(1)

или, другая форма представления:

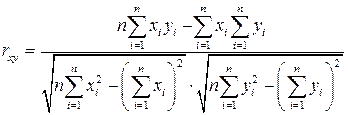(2)

В MS Excel коэффициент корреляции Пирсона вычисляется с помощью функции КОРРЕЛ(массив1;массив2).

Задача 1. 20 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Специалиста интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X – обозначает среднее время решения наглядно-образных, а переменная У – среднее время решения вербальных заданий тестов.

Решение. Представим исходные данные в виде таблицы 2, в которой введены дополнительные столбцы, необходимые для расчета по формуле (2).

№ испытуемого	Среднее время решение наглядно-образных заданий	Среднее время решение вербальных заданий	XY	X²	Y²
№ испытуемого	Х	Y	XY	X²	Y²
1	19	10	190	361	100
2	32	20	640	1024	400
3	33	17	561	1089	289
4	44	28	1232	1936	784
5	28	27	756	784	729
6	35	31	1085	1225	961
7	39	20	780	1521	400
8	39	25	975	1521	625
9	44	35	1540	1936	1225
10	44	43	1892	1936	1849
11	24	10	240	576	100
12	37	28	1036	1369	784
13	29	13	377	841	169
14	40	31	1240	1600	961
15	42	40	1680	1764	1600
16	32	24	768	1024	576
17	48	45	2160	2304	2025
18	42	26	1092	1764	676
19	33	16	528	1089	256
20	47	36	1692	2209	1296
Сумма	731	525	20464	27873	15805

Построим корреляционное поле

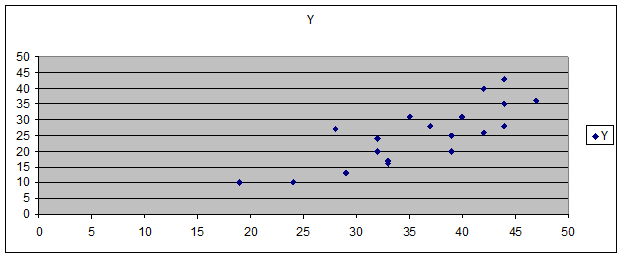
Можно предположить, что связь между переменными близка к линейной.

Рассчитываем эмпирическую величину коэффициента корреляции по формуле (2)

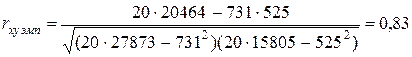
Т.о., связь между временем решения наглядно-образных и вербальных положительная, высокая. Полученная прямо пропорциональная зависимость говорит о том, что чем выше среднее время решения наглядно-образных задач, тем выше среднее время решения вербальных и наоборот.

Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.

2. Распределения переменных Х и У должны быть близки к нормальному.

3. Число варьирующих признаков в сравниваемых переменных X и У должно быть одинаковым.

Регрессионный анализ

Эмпирические математические модели. Математико-статистические идеи метода. Классификация многомерных методов по исходным предположениям о структуре данных. Линейная регрессия. Многофакторная линейная регрессия. Оценка уровней значимости коэффициентов регрессионного уравнения. Нелинейная регрессия.

Предположим, что при анализе некоторой экономической ситуации исследователь выдвигает предположение о существовании некоторой зависимости между двумя переменными. При этом одна их этих переменных считается зависимой (y) и рассматривается как функция от другой независимой переменной (х). На практике это соотношение, как правило, не является прямым: на переменную y кроме рассматриваемой детерминированной переменной х действует еще множество мелких факторов, которые по разным причинам не могут быть учтены в модели, но оказывают свое совокупное влияние на величину y. В эконометрическом анализе этот факт неточности соотношения между объясняющими и объясняемыми переменными признается путем явного включения в него случайного фактора, описываемого случайным остаточным членом u.

В общем случае эту зависимость можно представить в виде:

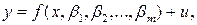(3.1)

где х – вектор наблюдений за независимой переменной (регрессор); ;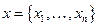

y – вектор наблюдений за зависимой переменной (регрессанд); ;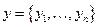

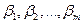- некоторый набор параметров;

n – количество наблюдений;

u – вектор случайных величин (ошибок); .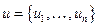

Регрессионная зависимость между двумя переменными вида (3.1) называется простой регрессией (однофакторной регрессионной моделью).

Для точного описания регрессионного уравнения необходимо знать условный закон распределения зависимой переменной y при условии, что переменная Х примет значение х, т.е. Х=х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений ( x_i, y_i) ограниченного объема n. В этом случае речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная линия регрессии:

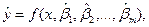(3.2)

При этом, величина 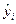интерпретируется как расчетное значение y, соответствующее наблюдаемой переменной х _i. Тогда ошибку (погрешность)регрессии для каждого наблюдения можно представить так:

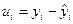(3.3)

Существует несколько причин существования случайной стохастической:

1. Значение переменной y определяется не только введенной в рассмотрение переменной х. Существует и другой значимый фактор (один или несколько), оказывающий существенное влияние на величину регрессанта.

2. На величину влияют случайные факторы, которые невозможно учесть или значение которых не могут быть оценены количественно.

3. Допущены ошибки спецификации.

4. Возможны, также, ошибки при сборе и измерении исходной информации.

Очевидно, что чем меньше и, тем точнее выборочное уравнение регрессии (3.2) характеризует экономический процесс.

Линейная зависимость

(а)	(б)

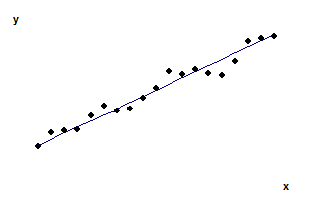
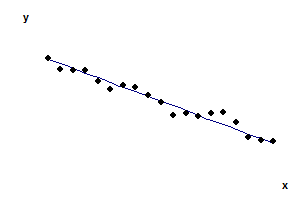
Рис. 1. Линейная регрессионная зависимость

Линейная зависимость предполагается, если при увеличении факторного признака ( x) происходит равномерное увеличение (рис.1а) или уменьшение (рис.1б) результативного признака ( y). В первом случае график этой зависимости – возрастающая прямая, а во втором – убывающая. При этом регрессионная зависимость ищется в виде

y= a+ bx, (3.4)

где b – тангенс угла наклона прямой, а коэффициент а – ордината точки пересечения прямой с осью Оy.

Для линейной зависимости характерен постоянный закон роста. Если рассчитывать первые приросты по формуле D y_i= y_i- y_i_-1, i=2,3,…, n, то они будут постоянной величиной.

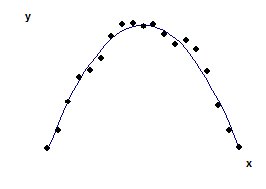
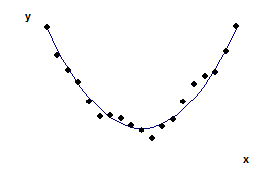
Квадратичная зависимость

(а)	(б)

Рис. 3. Квадратичная регрессионная зависимость

Когда уровень результативного признака возрастает, а затем, достигнув некоторого максимального значения, начинает примерно с той же скоростью убывать или, наоборот, наблюдается сначала уменьшение, а позднее – увеличение значения y, то выдвигается гипотеза о квадратичной зависимости

y= a+ bx +сх². (3.5)

Точки корреляционного поля при этом близки к выпуклой (рис. 3а) или вогнутой (рис. 3б) параболе.

В уравнении (3.5) параметр b называется линейным приростом, параметр с – ускорением роста.

Если первые приросты рассчитать для квадратичной зависимости, то они будут иметь линейную зависимость по аргументу и ряд из первых приростов D y₂, D y₃,…на графике будет представлен прямой линией. Вторые приросты D⁽²⁾ y_i= D u_i= u_i- u_i_-1, i=2,3,…, n для квадратичной функции будут постоянны. Значения приростов не зависят от значений самой функции, поэтому полиномиальные кривые роста можно использовать для аппроксимации экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

Обратная зависимость

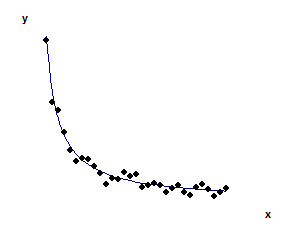
Рис. 4. Обратная регрессионная зависимость

Когда уровень результативного признака резко снижается до некоторого значения, а, затем, остается примерно на одном уровне, а кривая, проведенная через точки корреляционного поля напоминает гиперболу (рис.4), то предполагают обратную зависимость вида

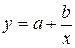. (3.7)