При исследовании большинства экономических процессов выясняется, что на объясняемую переменную существенное влияние оказывает не один, а несколько факторов. В этом случае говорят о многомерной (многофакторной) регрессионной модели (multiple regression model) или просто о множественной регрессии:
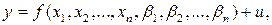 (4.1)
(4.1)
где y – эндогенная (или зависимая) переменная;
n – количество независимых переменных;
x1, x2,… xn – экзогенные (независимые) переменные (или факторы);
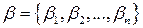 - некоторый набор параметров (константы, которые необходимо определить),
- некоторый набор параметров (константы, которые необходимо определить),
u – случайная величина (ошибка).
В множественной регрессионной модели регрессоры 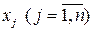 являются не случайными, а детерминированными переменными. Случайными переменными являются u и зависящая от нее y. Регрессанд y является, как правило, количественной переменной, область изменения которой не ограничена. Иногда y может быть качественной, шкалируемой (ранжируемой) величиной, например, экзаменационные оценки студентов, разряды гостиниц и т.п.
являются не случайными, а детерминированными переменными. Случайными переменными являются u и зависящая от нее y. Регрессанд y является, как правило, количественной переменной, область изменения которой не ограничена. Иногда y может быть качественной, шкалируемой (ранжируемой) величиной, например, экзаменационные оценки студентов, разряды гостиниц и т.п.
На практике чаще всего используются наиболее простые и наиболее разработанные в теории линейные многофакторные регрессионные модели.
Классической линейной многофакторной моделью называется регрессионная модель линейная по переменным и своим параметрам. В общем виде ее можно записать так:
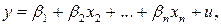 (4.2)
(4.2)
или
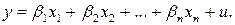 . (4.2')
. (4.2')
Здесь регрессор 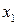 называется вспомогательным регрессором (вспомогательной переменной) для свободного члена
называется вспомогательным регрессором (вспомогательной переменной) для свободного члена 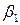 и принимает единичные значения.
и принимает единичные значения.
Параметры 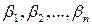 называют частичными коэффициентами регрессии.
называют частичными коэффициентами регрессии.
Проводить дальнейшие рассуждения удобно, если представить модель в матричном виде. Для этого введем обозначения:
| X= | - матрица наблюдений Х (или матрица плана), включающая значения (xij) j-го регрессора ( 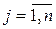 ) в i-м наблюдении ( ) в i-м наблюдении ( 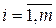 ) и единичный столбец коэффициентов при вспомогательной переменной х1 ( ) и единичный столбец коэффициентов при вспомогательной переменной х1 ( 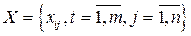 ) )
| |
Y= 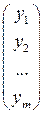
| - вектор – столбец значений у i регрессанта у в i-м наблюдении ( | |
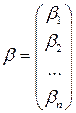
| - вектор неизвестных параметров модели ( | |
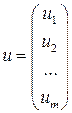
| - вектор – столбец остатков модели в каждом наблюдении ( | |
Учитывая введенные обозначения, запишем классическую эконометрическую модель (4.2) в матричной форме:
Y= X b+ u (4.3)
Статистические способы определения неизвестных параметров модели (4.3) основаны на предпосылках распределения случайной составляющей и. Но они не проверяются заранее. Уже после построения уравнения регрессии находят остатки модели ui, и только затем проводится проверка основных предпосылок применения одношагового метода наименьших квадратов.
Дата: 2019-03-05, просмотров: 306.
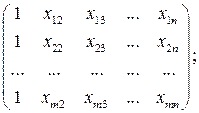
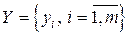 )
)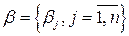 )
)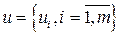 )
)