Первоначальное значение термина "корреляции" – взаимная связь. Когда говорят о корреляции, используют термины "корреляционная связь" и "корреляционная зависимость".

Корреляционная связь – это согласованные изменения двух признаков или большего количества признаков (множественная корреляционная связь).

Корреляционная связь отражает тот факт, что изменчивость одного признака находится в некотором соответствии с изменчивостью другого "Стохастическая[1] связь имеется тогда, когда каждому из значений одной случайной величины соответствует специфическое (условное) распределение вероятностей значений другой величины, и наоборот, каждому из значений этой другой величины соответствует специфическое (условное) распределение вероятностей значений первой случайной величины" (Суходольский Г.В., 1972, с. 178).

Корреляционная зависимость – это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.

Оба термина – корреляционная связь и корреляционная зависимость – часто используются как синонимы. Между тем, согласованные изменения признаков и отражающая это корреляционная связь между ними может свидетельствовать не о зависимости этих признаков между собой, а зависимости обоих этих признаков от какого-то третьего признака или сочетания признаков, не рассматриваемых в исследовании.

Зависимость подразумевает влияние, связь – любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной связи, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого, но находится ли причина изменений в одном из признаков или она оказывается за пределами исследуемой пары признаков, нам неизвестно. В большинстве случаев трудно определить, что в рассматриваемой паре признаков является независимой, а что – зависимой переменной.

Учитывая, что термин "зависимость" явно или неявно подразумевает влияние, лучше пользоваться более нейтральным термином "корреляционная связь".

Корреляционные связи различаются по форме, направлению и степени (силе).

По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи (см. Рис. 6.1). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности.

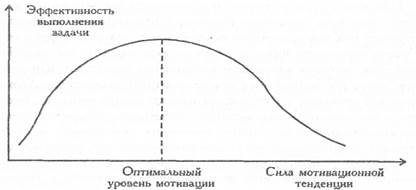
Рис. 1. Связь между эффективностью решения задачи и мотивационной тенденцией

По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака – низкие значения другого (см. Рис. 2-3). При отрицательной корреляции соотношения обратные.

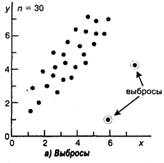
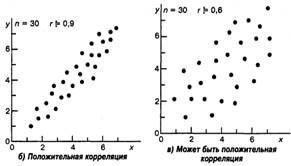Рис.2.

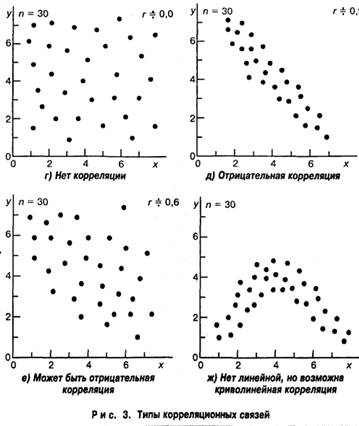
При положительной корреляции коэффициент корреляции имеет положительный знак, например r =+0,207, при отрицательной корреляции – отрицательный знак, например r=–0,207.

Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции.

Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции. Максимальное возможное абсолютное значение коэффициента корреляции r=1; минимальное r =0.

Общая классификация корреляционных связей (по Ивантер Э.В., Коросову А.В., 1992):

1) сильная, или тесная        при коэффициенте корреляции r³0,70;

2) средняя                           при 0,5£r<0,7;

3) умеренная                       при 0,3£r<0,5;

4) слабая                             при 0,2£r<0,3;

5) очень слабая                   при r<0,2.

Переменные X и У могут быть измерены в разных шкалах, именно это определяет выбор соответствующего коэффициента корреляции:

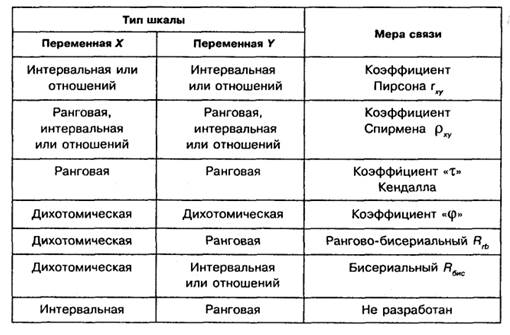
В практических исследованиях чаще всего применяется коэффициент линейной корреляции r Пирсона.

Ведь что, в сущности, мы доказываем, когда обосновываем различия в долях двух выборок, характеризующихся исследуемым эффектом? Мы показываем, что если испытуемый относится к одной из выборок, то скорее всего он будет характеризоваться какими-то определенными значениями исследуемого признака, а если он относится к другой из двух выборок, то он будет характеризоваться (с большой степенью вероятности) другими значениями исследуемого признака. Фактически мы исследуем сопряженные изменения двух признаков: отнесенность к той или иной выборке и определенные значения исследуемого признака.

Что мы доказываем, с другой стороны, когда два распределения признака оказываются сходными или, наоборот, статистически достоверно различающимися между собой? Мы доказываем, что в обеих выборках частоты встречаемости разных значений признака распределяются согласованно или, наоборот, несогласованно.