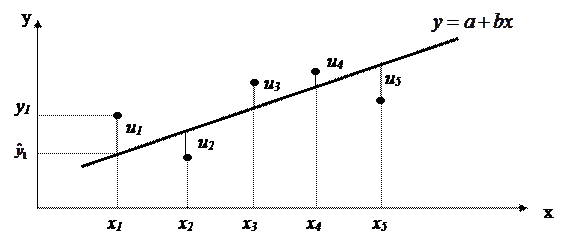
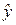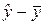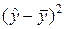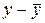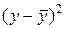Предположим, что этап спецификации модели пройден, в результате выдвинута гипотеза о линейной зависимости между объясняющей и объясняемой переменными. В этом случае говорят о простой линейной регрессии, или о линейной регрессионной модели с двумя переменными, которую в общем виде можно представить так:
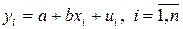 . (1)
. (1)
Для того чтобы получить явный вид модели необходимо знать неизвестные параметры этой модели.
Переходим к следующему этапу эконометрического анализа – к параметризации. Рассуждения будем проводить, используя форму представления модели в виде (1).
Построение линейной регрессии сводится к оценке ее параметров – а и b. Определить эти параметры можно различными способами. Как правило, оценка регрессионных коэффициентов эконометрической модели проводится на основе анализа остатков модели 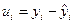 . Рассмотрим классический метод оценки параметров, называемый обычным или одношаговым методом наименьших квадратов (1МНК), Ordinary Least Squares, OLS.
. Рассмотрим классический метод оценки параметров, называемый обычным или одношаговым методом наименьших квадратов (1МНК), Ordinary Least Squares, OLS.
Замечание. Применение одношагового метода наименьших квадратов возможно при выполнении некоторых предпосылок, о которых речь пойдет в следующей главе. Там же будет показано, что параметры модели, оцененные с помощью 1МНК являются наиболее эффективными линейными оценками параметров a и b.
При графической интерпретации задача определения параметров модели сводится к отысканию такой прямой, которая как можно "точнее" будет отображать положение точек поля корреляции, т.е., разности между эмпирическими точками и точками построенной прямой (остатками) должны быть минимальными.
| |||
| Рис.6. Остатки линии регрессии |
Минимизировать сумму остатков не имеет смысла, так как остатки имеют различные знаки и при суммировании "аннулируют" друг друга и если выбрать в качестве параметра а среднее значение регрессанта ( 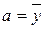 ), а b принять равной нулю (b=0), то сумма будет автоматически равна своему минимальному значению – нулю. Для того чтобы "нейтрализовать" действие противоположных знаков, в качестве меры адаптации регрессионной модели
), а b принять равной нулю (b=0), то сумма будет автоматически равна своему минимальному значению – нулю. Для того чтобы "нейтрализовать" действие противоположных знаков, в качестве меры адаптации регрессионной модели 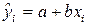 к эмпирическим данным применяется сумма квадратов остатков (ошибок), error sum of squares, (ESS):
к эмпирическим данным применяется сумма квадратов остатков (ошибок), error sum of squares, (ESS):
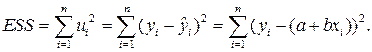 (2)
(2)
Запишем необходимые условия экстремума (First Order Conditition, FOC):
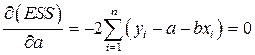 ; (3)
; (3)
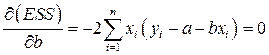 ,
,
или 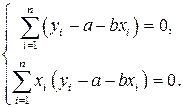 (4)
(4)
После раскрытия скобок получаем стандартную форму нормальных уравнений (индекс суммирования опущен):
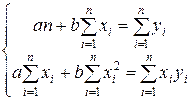 (5)
(5)
решая систему (3.14) находим оценки параметров модели:
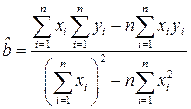 (6)
(6)
Параметр 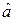 можно получить:
можно получить:
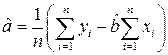 (7)
(7)
Полученные формулы (3.16)-(3.17) чаще других используют при определении параметров простой линейной эконометрической модели.
Из уравнения (3.17) следует
 (8)
(8)
или 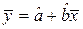 (9)
(9)
где 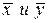 средние значения
средние значения 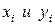 .
.
Таким образом, прямая линия регрессии проходит через точку средних значений 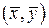 .
.
Учитывая этот факт, можно воспользоваться и альтернативным способом отыскания параметров модели, основанном на том факте, что линия регрессии проходит через точку средних значений 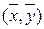 .
.
Разделим обе части системы уравнений (3.14) на n, получим
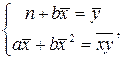 (9)
(9)
где средние 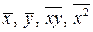 определяются по известным формулам:
определяются по известным формулам:
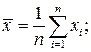
| 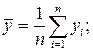
|
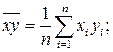
| 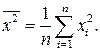
|
Решая систему (3.18), получим:
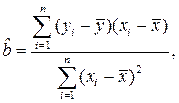 (10)
(10)
 (11)
(11)
Коэффициент 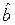 называется выборочным коэффициентом регрессии или просто коэффициентом регрессии у по х. Он показывает, на сколько единиц в среднем изменится переменная у при увеличении переменной х на одну единицу.
называется выборочным коэффициентом регрессии или просто коэффициентом регрессии у по х. Он показывает, на сколько единиц в среднем изменится переменная у при увеличении переменной х на одну единицу.
Для оценоки точности модели, мерой качества уравнения регрессии и характеристикой прогностической силы анализируемой регрессионной модели используют коэффициент детерминации R2.
Коэффициентом детерминации называется величина
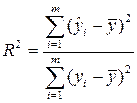 , (3.41)
, (3.41)
Величина R2 показывает какая часть вариации регрессанта может быть объяснена вариацией выбранного регрессора и характеризует качество подгонки регрессионной модели к наблюдаемым значениям y. В следующей главе будет показано, что 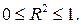 Если
Если 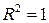 , то это означает точную подгонку, между переменными существует линейная связь, все
, то это означает точную подгонку, между переменными существует линейная связь, все 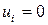 . Если
. Если 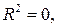 то говорят, что функция регрессии не объясняет ничего. Если
то говорят, что функция регрессии не объясняет ничего. Если  , то регрессионное уравнение оценено тем лучше, чем больше при прочих равных условиях R2.
, то регрессионное уравнение оценено тем лучше, чем больше при прочих равных условиях R2.
Задача 2. Найти корреляционную зависимость между временем решения наглядно-образных (Х), и вербальных У заданий тестов по данным из задачи 1. Оценить качество модели.
Решение.
Коэффициент корреляции между Х и У высокий ( 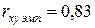 ). Выдвигаем гипотезу о линейной зависимости между переменными. Уравнение будем искать в виде:
). Выдвигаем гипотезу о линейной зависимости между переменными. Уравнение будем искать в виде:
y = a + bx .
Параметры будем находить по формулам:
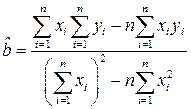 (6)
(6)
(функция НАКЛОН(известные_значения_y;известные_значения_x)
Параметр 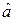 можно получить:
можно получить:
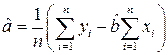 (7)
(7)
(функция ОТРЕЗОК(известные_значения_x;известные_значения_y))
Будем использовать расчетную таблицу из задачи 1
| № испытуемого | Среднее время решение наглядно-образных заданий | Среднее время решение вербальных заданий | XY | X2 | Y2 |
| Х | Y | ||||
| ... | ... | ... | ... | ... | ... |
| Сумма | 731 | 525 | 20464 | 27873 | 15805 |
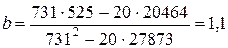 ,
,
 .
.
Уравнение регрессии имеет вид:
y=–14,1+1,1х.
Рассчитаем теоретические значения y и построим полученную прямую на корреляционном поле
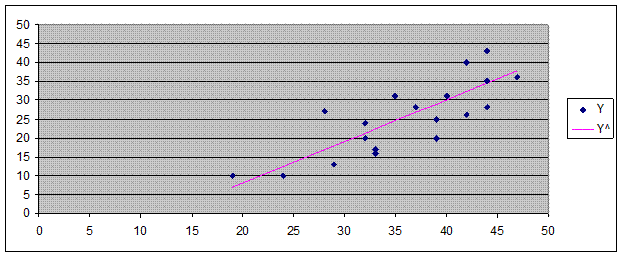
Для оценки качества модели рассчитаем коэффициент детерминации:
| № испытуемого | y |
|
|
|
|
|
| 1 | 10 | 6,9 | -19,4 | 375,51 | -16,25 | 264,06 |
| 2 | 20 | 21,2 | -5,0 | 25,24 | -6,25 | 39,06 |
| 3 | 17 | 22,3 | -3,9 | 15,36 | -9,25 | 85,56 |
| 4 | 28 | 34,5 | 8,2 | 67,67 | 1,75 | 3,06 |
| 5 | 27 | 16,8 | -9,4 | 89,12 | 0,75 | 0,56 |
| 6 | 31 | 24,5 | -1,7 | 2,93 | 4,75 | 22,56 |
| 7 | 20 | 29,0 | 2,7 | 7,32 | -6,25 | 39,06 |
| 8 | 25 | 29,0 | 2,7 | 7,32 | -1,25 | 1,56 |
| 9 | 35 | 34,5 | 8,2 | 67,67 | 8,75 | 76,56 |
| 10 | 43 | 34,5 | 8,2 | 67,67 | 16,75 | 280,56 |
| 11 | 10 | 12,4 | -13,9 | 192,02 | -16,25 | 264,06 |
| 12 | 28 | 26,7 | 0,5 | 0,25 | 1,75 | 3,06 |
| 13 | 13 | 17,9 | -8,3 | 69,50 | -13,25 | 175,56 |
| 14 | 31 | 30,1 | 3,8 | 14,51 | 4,75 | 22,56 |
| 15 | 40 | 32,3 | 6,0 | 36,21 | 13,75 | 189,06 |
| 16 | 24 | 21,2 | -5,0 | 25,24 | -2,25 | 5,06 |
| 17 | 45 | 38,9 | 12,6 | 159,84 | 18,75 | 351,56 |
| 18 | 26 | 32,3 | 6,0 | 36,21 | -0,25 | 0,06 |
| 19 | 16 | 22,3 | -3,9 | 15,36 | -10,25 | 105,06 |
| 20 | 36 | 37,8 | 11,5 | 133,14 | 9,75 | 95,06 |
| Сумма | 525 | 525 | 0,00 | 1408,08 | 0,00 | 2023,75 |
| Среднее | 26,25 |
|
|
|
|
|

Коэффициент близок к 1, следовательно, модель достаточно точно демонстрирует корреляционную связь между временем решения наглядно-образных (Х), и вербальных (У) заданий тестов и имеет большую прогноститескую силу.
Дата: 2019-03-05, просмотров: 312.