Операционное или так называемое символическое исчисление возникло конце XI Автор исчисления английский инженер -электрик О.Хевис (1850-1925) изложил его в виде ряда формальных правил без глубокого математического обоснования. В 20 -х годах двадцатого столетия было установлено, что в основе операционного исчисления лежат интегральные преобразования - одно из наиболее мощных и широко используемых математических средств решения различных прикладных задач. Суть операционного исчисления состоит в том, что исследование функции f (x) заменяется исследованием интегрального преобразования Лапласа.
При этом, как правило, сложные уравнения f(x) превращаются в простые соотношения для ее интегрального преобразования. Например: аналитические действия интегрирования и дифференцирования заменяют совокупностью алгебраических операций, что в значительной мере упрощает исследуемую задачу. В связи с этим операционное исчисление нашло многостороннее и плодотворное использование в прикладной математике, физике, электро- и радиотехнике, а так же в других инженерных дисциплинах.
Теорема подобия. Если 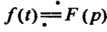 И
И 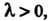 То умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число:
То умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число:
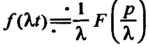
Теорема смещения. Если 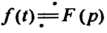 И
И 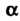 - произвольное комплексное число, то изменение (смещение) аргумента изображения на величину а приводит к умножению оригинала на величину
- произвольное комплексное число, то изменение (смещение) аргумента изображения на величину а приводит к умножению оригинала на величину 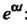
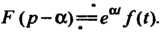
Теорема запаздывания. Если 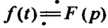 И
И 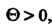 То запаздывание аргумента оригинала на положительное число
То запаздывание аргумента оригинала на положительное число 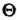 Приводит к умножению изображения на величину
Приводит к умножению изображения на величину 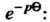
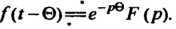
Теорема умножения. Если 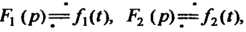 То
То
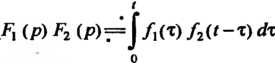
Таблица соответствия оригиналов и соответствия приведена на стр. 53 Приложение 3. Операционное исчисление.pdf
IV.5 Преобразования Лапласа
При исследовании и расчетах систем автоматического регулирования используется операционная форма записи. Она основана на использовании преобразования Лапласа. Преобразование Лапласа позволяет функцию x(t) одного переменного (времени t) преобразовать в функцию другого переменного x(s) (где s=a+jb – комплексное число) посредством соотношения:
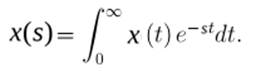
Функцияx f (t) называется оригиналом, а x(s) – изображением. Сокращенно преобразование Лапласа записывается как
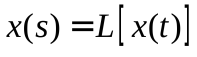
Обратная операция, т.е. нахождение функци иx (t) по ее изображению x(s) называется обратным преобразованием Лапласа:
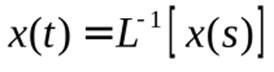
При использовании преобразования Лапласа первая производная от x будет иметь изображение 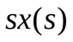 , вторая
, вторая 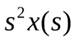 , третья
, третья 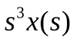 и т.д. Интеграл от
и т.д. Интеграл от 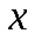 будет иметь изображение
будет иметь изображение 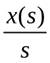 . Если применить преобразование Лапласа к дифференциальному уравнению, то при нулевых начальных условиях оно примет вид
. Если применить преобразование Лапласа к дифференциальному уравнению, то при нулевых начальных условиях оно примет вид 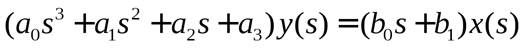 .
.
Это уравнение — алгебраическое, в нем s является независимой комплексной переменной, а величины х(s) и y(s) являются только изображениями физических величин х (t )и y(t). Символ s является алгебраическим числом.
Операционная форма записи уравнений элементов проста и удобна, так как преобразовать и решить алгебраическое уравнение несравненно проще, чем дифференциальное. Именно это и обеспечило ее широкое применение в теории автоматического управления.
Для оценки динамики систем служит также операционное уравнение, из которого получается передаточная функция - отношение изображения выходной величины к изображению входной величины системы.
Если, например, операционное уравнение имеет вид
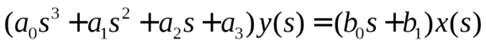 ,
,
то передаточная функция системы
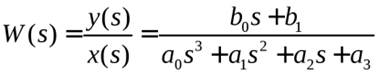 .
.
Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета САР сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных объектов управления. В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случаев качественную работу реальной системы управления.
В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним из трех видов передаточной функции обьекта управления:
1. В виде передаточной функции инерционного звена первого порядка:
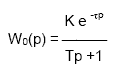
где: К - коэффициент усиления,
Т - постоянная времени, - запаздывание,
которые должны быть определены в окрестности номинального режима работы объекта.
2. Для объекта управления без самовыравнивания передаточная функция имеет вид:
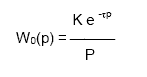
3. Более точнее динамику обьекта описывает модель второго порядка с запаздыванием:
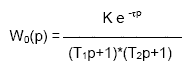
Дата: 2019-03-05, просмотров: 398.