Типовые динамические звенья являются основными элементарными составными частями абстрактных структур непрерывных систем управления, поэтому знание их характеристик облегчает анализ и синтез таких систем.

Типовыми динамическими звеньями называются звенья, описываемые дифференциальным уравнением не выше второго порядка. Такие звенья классифицируются в зависимости от вида левой и правой частей их дифференциального уравнения. Все типовые звенья можно разделить на три группы: позиционные, интегрирующие и дифференцирующие. Каждая из групп в свою очередь содержит несколько типовых звеньев.

Тип динамического звена, соответствующего реальному устройству, зависит от принятых допущений и выбора входной и выходной величин этого устройства. Одно и то же устройство в зависимости от степени его идеализации может быть отнесено к различным типам динамических звеньев.

Рассмотрим наиболее часто встречающиеся на практике типовые динамические звенья и определим для каждого из них основные характеристики: дифференциальное уравнение; передаточную функцию; переходную функцию; функцию веса; амплитудно-фазовую, амплитудную, фазовую и логарифмические частотные характеристики. Названия и вид дифференциальных уравнений типовых звеньев приведены в табл. 4.1.

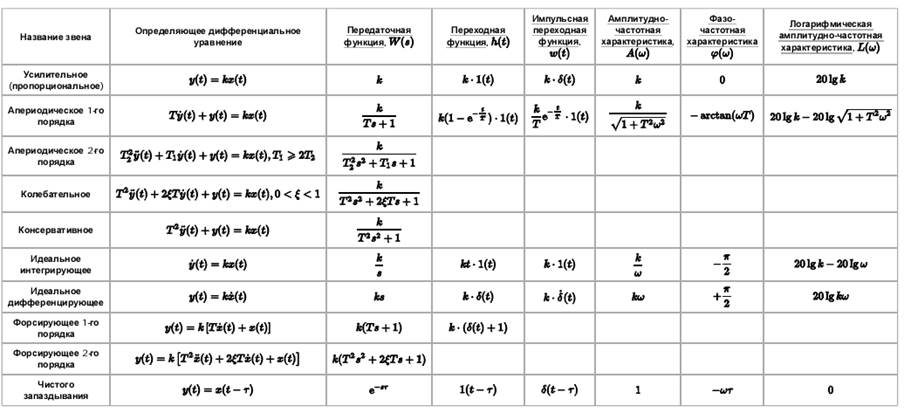
Таблица 4.1. Типовые динамические звенья

IV.3 Передаточная функция

Передаточная функция линейной стационарной системы управления (системы автоматич. регулирования) – преобразованная формула отклика системы на воздействие единичной импульсной функции (дельта-функции) при нулевых условиях в момент t=0 (сам этот отклик наз. функцией веса, импульсной переходной функцией или импульсной характеристикой системы). Эквивалентное определение: передаточной функции есть отношение изображений по Лапласу (см. Операционное исчисление).выходного и входного сигналов с нулевыми начальными данными. Передаточная функция представляет собой дробно-рациональную функцию W(p) комплексного переменного р (s); она является коэффициентом в линейном соотношении

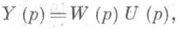(1)

связывающем изображение по Лапласу U(р) входа системы (воздействия, управления) и(t).и изображение по Лапласу Y(р).выхода системы (отклика, реакции) y(t).с нулевыми начальными значениями. В теории управления соотношение (1) принято изображать графически (см. рис.).

Пусть, например, система управления описывается линейным обыкновенным дифференциальным уравнением с постоянными коэффициентами

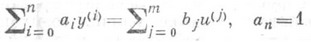(2) (в реальных системах, как правило, ).

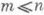Тогда

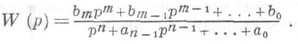(3)

Это же выражение можно получить, если, используя операторную форму записи уравнения (2) с помощью оператора дифференцирования р

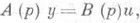определить П. ф. как отношение входного оператора системы В(р) к собственному оператору системы (р). П. ф. (3) системы (2) допускает следующее толкование: если выбрать управление 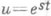, где s - комплексное число такое, что 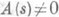, то линейное неоднородное уравнение (2) имеет частное решение .

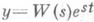Передаточную функцию не следует путать с переходной функцией, к-рая представляет собой отклик системы на воздействие единичной ступенчатой ф у н к ц и и

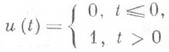
при нулевых начальных условиях.

Передаточная функция является одним из основных понятий теории линейных стационарных систем управления. Она не зависит от характера приложенных к системе управляющих воздействий, а определяется лишь параметрами самой системы и дает тем самым ее динамич. характеристику. Особую роль в теории управления играет функция W(iw) чисто мнимого аргумента, наз. амплитудно-фазовой, или частотной, характеристикой системы. Понятие П. ф. обобщается и на линейные системы управления иных типов (матричные, нестационарные, дискретные, с распределенными параметрами и др.).