Основным недостатком рассмотренного алгебраического подхода к анализу устойчивости является то, что в сложных системах управления трудно установить связь между корнями знаменателя рk , k=1, 2, …, n, и параметрами элементарных звеньев, составляющих систему управления. Это приводит к трудностям коррекции неустойчивых систем. Для того, чтобы упростить анализ устойчивости, желательно проводить этот анализ по передаточной функции H(p) разомкнутой системы управления.

В 1932 г. американский ученый Найквист разработал эффективный метод анализа устойчивости усилителей с обратной связью. В 1938 г. советский ученый А.В. Михайлов обобщил метод Найквиста на замкнутые системы автоматического управления.

Критерий Найквиста основан на построении годографа передаточной функции H(jw) разомкнутой системы управления. Годографом передаточной функции H(jw) называется кривая, прочерчиваемая концом вектора H(jw) =|H(jw)|ejj(w) на комплексной плоскости при измерении частоты w от 0 до бесконечности.

Наиболее просто формулируется критерий устойчивости Найквиста: замкнутая система управления устойчива, если годограф передаточной функции H(jw) разомкнутой системы не охватывает на комплексной плоскости точку c координатами (-1, j0). На рисунках показаны примеры годографов устойчивой (рис. 16,а) и неустойчивой (рис. 16,б) систем управления.

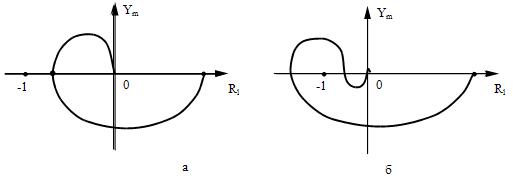
Рис. 16.

Если годограф проходит через точку -1, то говорят, что система находится на границе устойчивости. В этом случае на некоторой частоте H(jw0)= -1 и в системе могут существовать незатухающие колебания частоты w0. В неустойчивых системах уровень сигнала x(t) будет нарастать со временем. В устойчивых - уменьшаться.

Запас устойчивости

Еще одним достоинством рассматриваемого критерия является возможность определения запаса устойчивости системы управления. Запас устойчивости характеризуют двумя показателями: запасом устойчивости по усилению и запасом устойчивости по фазе.

Запас устойчивости по усилению определяется величиной g =1/|H(jw0)|, где w0 - частота, на которой 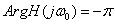(рис. 17,а). Запас устойчивости g показывает, во сколько раз должен измениться (увеличиться) модуль передаточной функции разомкнутой системы управления, чтобы замкнутая система оказалась на границе устойчивости. Требуемый запас устойчивости зависит от того, насколько в процессе работы может возрастать коэффициент передачи системы по сравнению с расчетным.

Запас устойчивости по фазе оценивается величиной угла 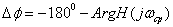, где частота wсp , называемая частотой среза, определяется условием |H(jwcp)|=1 (рис. 17, б).

Величина Dj показывает, насколько должна измениться фазовая характеристика разомкнутой системы управления, чтобы замкнутая система оказалась на границе устойчивости. Запас устойчивости по фазе обычно считается достаточным, если
|Dj| ³ 30o.

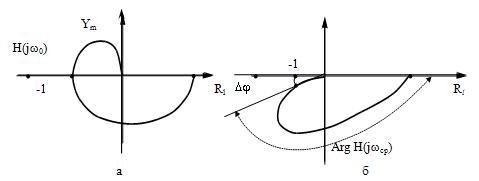
Рис. 17.