Амплитудно-частотная и фазочастотная характеристики

Предположим, что на вход цепи было подано гармоническое воздействие с амплитудой A₁:

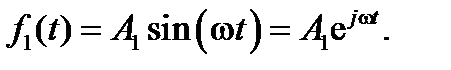                                                         (1.5.1)

    Тогда сигнал на ее выходе также будет являться гармоническим, но с амплитудой A₂ и сдвинутым на ψ по отношению к исходному:

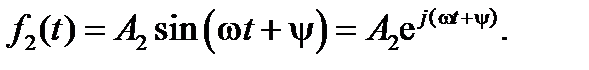                                               (1.5.2)

Определим отношение амплитуды выходной величины к входной:

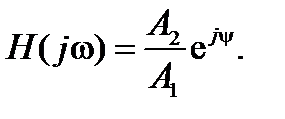                                                                     (1.5.3)

Выражение (1.5.3) можно представить в другом виде:

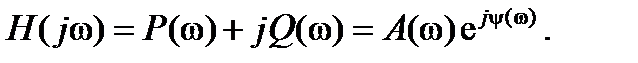                                                        (1.5.4)

           Формулы (1.5.3) и (1.5.4) эквивалентны. Переменная H(jω) представляет собой частотную характеристику системы, а P(ω) и Q(ω) – действительная и мнимая ее части соответственно. Величина A(ω) представляет собой зависимость амплитуды выходного сигнала от частоты ω входного сигнала и называется амплитудно-частотной характеристикой, а ψ(ω) – зависимость сдвига фаз выходного сигнала по отношению к входному от частоты ω последнего и является фазочастотной характеристикой.

Зная значения вещественной и мнимой частей частотной передаточной функции P(ω) и Q(ω), A(ω) и ψ(ω) можно получить из выражений:

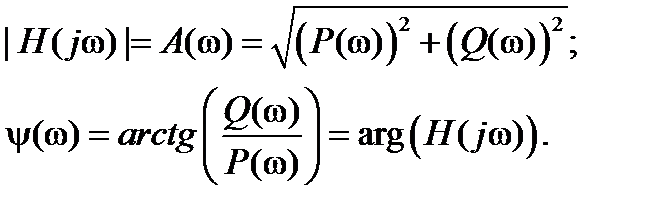                                                      (1.5.5)

На практике удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазочастотную характеристику (ЛФЧХ):

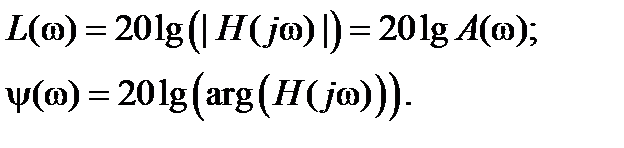                                           (1.5.6)

Эта величина выражается в децибелах (дБ). Бел представляет собой логарифмическую единицу, соответствующую увеличению мощности в 10 раз, следовательно, два бела – в 100 раз, три бела – в 1000 раз и т. д.

Пример расчета частотных характеристик в ППП Mathcad 15.

Произведем расчет частотных характеристик длинной линии. В качестве примера возьмем ситуацию, когда на ее вход подается ступенчатый сигнал E_m·1(t). Его изображение по Лапласу имеет вид:

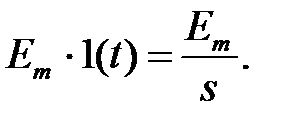                                                                                          (1.5.7)

Умножая правую часть на K_u(s) и, заменяя s=jω, получим частотную характеристику:

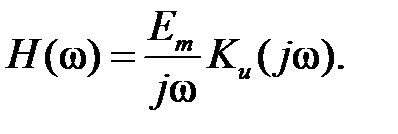                                                                                (1.5.8)

       В Mathcad можно получить выражение (1.5.8) в параметрическом виде как функцию частоты. Для этого применяется оператор «simplify» из панели «Символьные». Аналогично преобразованию Лапласа (см. пункт 1.4), сначала вводится выражение «H(ω):=», затем вместо черного прямоугольника заносится правая часть выражения (1.5.8). Вычисления происходит автоматически (рис. 1.5.1). Сокращение количества знаков после запятой можно выполнить с применением меню «Формат»→«Результат» (см. пункт 1.4).

    Проверку правильности построения указанных характеристик можно проверить как графическим, так и аналитическим способами. При этом точка их перегиба обязательно должна находиться при частоте 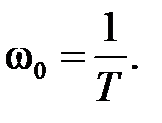 Найти ее можно в выражении U_L1(t) в степени экспоненты и без знака «-» (см. рис. 1.4.2). В нашем примере эта точка равна ω₀=21.865E+009.

    Для нахождения точки перегиба аналитически заменим аргумент ω на x в целях того, чтобы отличать два способа.  Напишем две функции |A1(x)| =|H(x)| и |A2(x)| =|H(21.865E+009)| – для АЧХ, |F1(x)| = arg(H(x)) и |F2(x)| =arg(H(21.865E+009)) – для ФЧХ. Условием пересечения данных графиков является равенство нулю их разности:

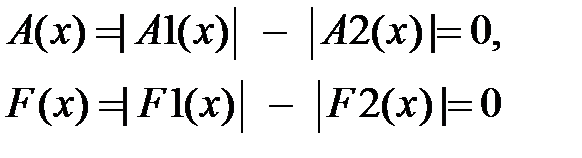                                                              (1.5.9)

Решая уравнения (1.5.9) относительно x, получают точку перегиба. Для нахождения корней уравнения x может быть применена функция ω_A=root(A(x),x) – для АЧХ и ω_F=root(F(x),x). Вместо x необходимо задавать начальное приближение, близкое к числу 21.865E+009. Например, 21·10⁹.

Из результатов вычисления (рис. 1.5.1) видно, что найденные решения практически совпадают с точкой ω₀: ω_A=2,187·10¹⁰≈21.865E+009, ω_F=2,186·10¹⁰≈21.865E+009.

Рис 1.5.1. Пример расчета частотной характеристики длинной линии

Для построения АЧХ требуется записать на оси ординат модуль характеристики |H(ω)|, а ФЧХ – ее аргумент arg(H(ω)). Их удобно представлять в логарифмическом масштабе. Для этого в свойствах графика необходимо поставить галочку напротив «Логарифмический масштаб» под надписью «Ось X» и «Основная ось Y».

    Лучше построить сразу на одном графике модуль |H(ω)| и его значение в зависимости от найденной точки |H(ω₀)| =|H(21.865E+009)|. Понятно, что последняя характеристика будет представлять из себя прямую, параллельную оси абсцисс (рис. 1.5.2). Аналогично строятся два графика для ФЧХ arg(H(ω)) и arg(H(21.865E+009)) (рис. 1.5.3).

Рис 1.5.2. Амплитудно-частотная характеристика длинной линии

Рис 1.5.3. Фазочастотная характеристика длинной линии