Для исследования реакции системы на идеальный периодический сигнал (см. рис. 1.3.3, а) в целях упрощения будем рассматривать только последовательность двух импульсов, поэтому переходная характеристика каждого из них будет полностью совпадать с (1.4.8).
Сигнал, повторяющийся через период T можно сформировать как разность двух импульсов h1(t) и h2(t) (рис. 1.4.1):
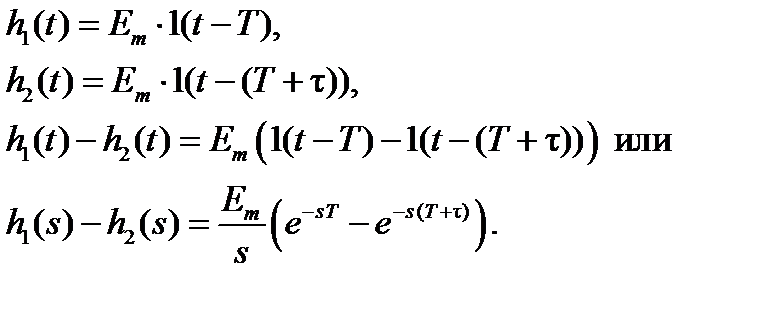 (1.4.13)
(1.4.13)
Его описание имеет следующий вид:
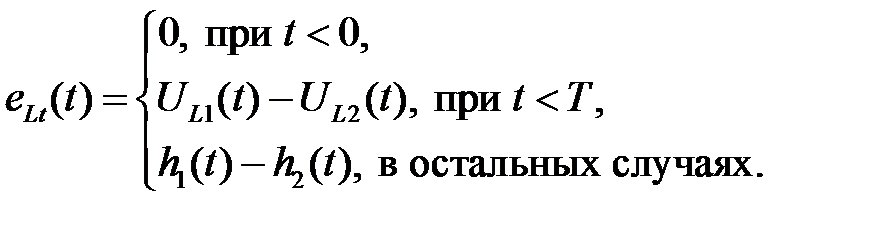 (1.4.14)
(1.4.14)
Представление реакции системы на периодический сигнал, представленный в виде разложения в ряд Фурье приведем для четной функции. При этом необходимо использовать выражение для коэффициента (1.4.10).
Производя в (1.4.15) замену  , получим переходную характеристику:
, получим переходную характеристику:
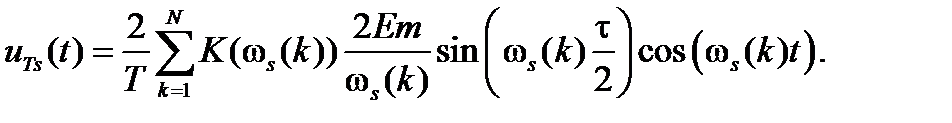 (1.4.15)
(1.4.15)
где N – число гармоник;
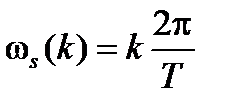 – частота на k-ой гармоники.
– частота на k-ой гармоники.
При выполнении курсовой работы для описания входных и выходных воздействий импульсного и периодического сигналов студенту предоставляется возможность выбора одного из двух типов сигнала: симметричный или несимметричный.
| 0 |
| t |
| t |
| 0 |
| Em |
| h1(t) |
| T |
| Em |
| h2(t) |
| τ |
| 0 |
| t |
| h1(t)- h2(t) |
| Em |
Рис 1.4.1. Формирование периодически повторяющегося импульса.
Пример расчета реакции системы в ППП Mathcad 15.
Для исследования переходных процессов, отражающих реакцию на идеальный периодический сигнал используем выражения (1.4.4) – (1.4.9), а на приближенный – (1.4.10), (1.4.11).
Обратное преобразование Лапласа осуществляется в программе при помощи команды на панели «Символьные» под названием «inv laplace». Cначала пишется буквенное обозначение сигнала, затем знак присваивания, например «UL 1(t):=», а далее вызывается указанный оператор и слева от него, вместо черной точки вводится функция U1(s). Произойдет автоматическое преобразование. Результат отобразится после стрелки, стоящей справа от inv laplace.
По умолчанию Mathcad оставляет большое количество знаков после запятой, и при таких расчетах решение отображается зачастую на нескольких страницах. Для обеспечения более компактного отображения следует выполнить некоторую последовательность действий: поставить курсор на какое-нибудь числовое значение в вычисленном выражении после стрелки, далее нажать в меню «Формат»→»Результат». На вкладке «Формат числа» выбрать «Дробь», установить уровень точности, например, 3, поставить галочку напротив фразы «Применять в символьных результатах». Также на данной вкладке можно выбрать форматы «Научный» или «Инженерный» и отметить флаг «Показатели степени в виде E±000».
Пример расчета параметров реакции на импульсный сигнал приведен на рис. 1.4.2.

Рис. 1.4.2. Расчет параметров реакции на импульсный сигнал
Зависимость модуля коэффициента усиления от частоты |Ku(ω)| показана на рис. 1.4.3, откуда следует, что на частоте ω<108 рад/с он достаточно близок к 1. Поэтому установившееся значение реакции системы будет мало отличаться от амплитуды входного импульса.
В области частот ω>108 рад/с коэффициент усиления начинает резко снижаться (рис. 1.4.4).
Графики реакций системы us(t), h(t)=UL 1(t)-UL 2(t) на импульсные сигналы e(t), es(t) приведены на рис. 1.4.5, 1.4.6. Число гармоник N взято равным 15.
|
|
Рис. 1.4.3. Коэффициент усиления длинной линии на частоте ω<108 рад/с
|
|
Рис. 1.4.4. Коэффициент усиления длинной линии на частоте ω>108 рад/с
|
|
Рис. 1.4.5. Реакция системы на идеальный импульсный сигнал.
|
|
Рис. 1.4.6. Реакция системы на импульсный сигнал, представленный разложением в ряд Фурье при N=15.
Для расчета реакции на периодический сигнал удобно сначала найти преобразование Лапласа от функций h1(t) и h2(t), а затем построить переходную характеристику eLt(t) согласно условию (1.4.14), а uTs(t) – согласно (1.4.15). Пример ее вычисления показан на рис. 1.4.7. Графики реакций системы на указанные периодические сигналы приведены на рис. 1.4.8, 1.4.9. Число гармоник N также равно 15.

Рис. 1.4.7. Расчет параметров реакции на импульсный сигнал
|
|
 Рис. 1.4.8. Реакция системы на идеальный периодический сигнал.
Рис. 1.4.8. Реакция системы на идеальный периодический сигнал.
|
|
Рис. 1.4.9. Реакция системы на периодический сигнал, представленный разложением в ряд Фурье при N=15.
Дата: 2019-03-05, просмотров: 340.




