Н.В. Осипова
Исследование однородной линии передачи с распределенными параметрами
Электронное учебное издание
Методические указания к курсовой работе
по дисциплине «Электротехника»
Москва
УДК 621.3.011.711
УДК 621.3.011.715
УДК 621.3.012.6 — 621.3.012.8
Рецензент:
Осипова Н. В.
Исследование однородной линии передачи с распределенными параметрами. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2016. 60 с.
Представлены основные теоретические сведения об однородных электрических цепях с распределенными параметрами. Приведены примеры расчета и математического моделирования электротехнического устройства с использованием длинной линии в пакете прикладных программ MathCad 15.
Для студентов МГТУ имени Н.Э. Баумана, обучающихся по специальности "Информационные системы и технологии".
Рекомендовано учебно-методической комиссией факультета «Информатика и системы управления» МГТУ им. Н.Э. Баумана
Электронное учебное издание
Осипова Нина Витальевна
Исследование однородной линии передачи с распределенными параметрами
© 2016 МГТУ имени Н.Э. Баумана
Оглавление
Введение. 3
1. Теоретическая часть. 5
1.1. Классификация линий передачи. 5
1.2 Расчет параметров длинной линии. 9
1.3. Описание входных сигналов. 21
1.4 Описание выходных сигналов. 32
1.5 Частотные характеристики длинной линии. 41
1.6 Оценка качества работы длинной линии. 46
2. Требования к курсовой работе. 49
2.1 Примеры заданий на курсовую работу. 49
2.2 Требования к выполнению курсовой работы.. 51
2.3 Требования к оформлению курсовой работы.. 52
2.4 Требования к защите и оценке курсовой работы.. 53
3. Контрольные вопросы к защите курсовой работы.. 53
Заключение. 55
Список литературы.. 57
Приложения. 58
Введение
Целью написания курсовой работы является закрепление знаний, полученных при изучении курса лекций и лабораторного практикума. Основная ее задача состоит в приобретении навыков по составлению принципиальных схем электронных устройств, выполнению электрического расчета и моделированию.
В соответствии с утвержденными учебными планами студенты специальности ИУ выполняют курсовую работу по дисциплине «Электротехника» на 2 курсе, 4 семестре.
Общий объем работы должен составлять 20 – 25 страниц машинописного текста.
Структура курсовой работы:
1.Расчетно-пояснительная записка.
2. Задание.
3. Содержание.
4. Введение.
5. Расчет параметров длинной линии.
5.1 Первичные параметры.
5.2 Вторичные параметры.
6. Описание входных сигналов.
6.1 Ступенчатое воздействие.
6.2 Периодический сигнал.
7. Описание выходных сигналов.
5.1 Реакция системы на импульсный сигнал.
5.2. Реакция системы на периодический сигнал.
8. Частотные характеристики длинной линии.
8.1 Амплитудно-частотная характеристика.
8.2 Фазо-частотная характеристика.
9. Оценка качества работы длинной линии.
10. Выводы и заключение.
11. Список используемой литературы.
Этапы выполнения курсовой работы:
1. Получение индивидуального задания на курсовую работу.
2. Составление календарного графика выполнения курсовой работы, расписания консультаций.
3. Выполнение и сдача 1 модуля: «Расчет параметров длинной линии».
4. Выполнение и сдача 2 модуля: «Описание входных сигналов».
5. Выполнение и сдача 3 модуля: «Описание выходных сигналов».
6. Выполнение и сдача 4 модуля: «Расчет частотных характеристик длинной линии и оценка качества ее работы».
7. Оформление и сдача курсовой работы в печатном виде в соответствии со структурой, приведенной выше.
Теоретическая часть
Вторичные параметры линии.
К вторичным параметрам длинной линии относятся:
- коэффициент распространения γ, 1/м;
- коэффициент ослабления – α, Нп/м;
- коэффициент фазы – β, рад/м;
- модуль волнового сопротивления, |Zв|, Ом;
- фаза волнового сопротивления, Ψ, рад.
Коэффициент распространения γ показывает изменение величины напряжения бегущей волны и его фазовый сдвиг на единицу длины линии.
Коэффициент ослабления α показывает, во сколько раз выходная мощность сигнала в схеме меньше входной (в данном случае на участке dl). Измеряется обычно в дБ, но применяется также и величина, называемая Непером (1 Нп=8,685889638 дБ).
Коэффициент фазы (фазовая постоянная) β характеризует изменение угла вектора тока или напряжения на участке линии элементарной длины dl.
Волновое сопротивление длинной линии Zв определяется отношением амплитуды напряжения падающей, отраженной или бегущей волны к амплитуде силы тока той же волны. При расчетах используется только модуль данной величины |Zв|.
Фаза волнового сопротивления Ψ характеризует разность фаз волн напряжения и тока.
Для их вычисления необходимо иметь зависимости C0, L0, R0(ω) и G0(ω), найденные на предыдущем этапе, следовательно, параметры γ, α, Zв, Ψ также будут являться функциями круговой частоты ω [7]:
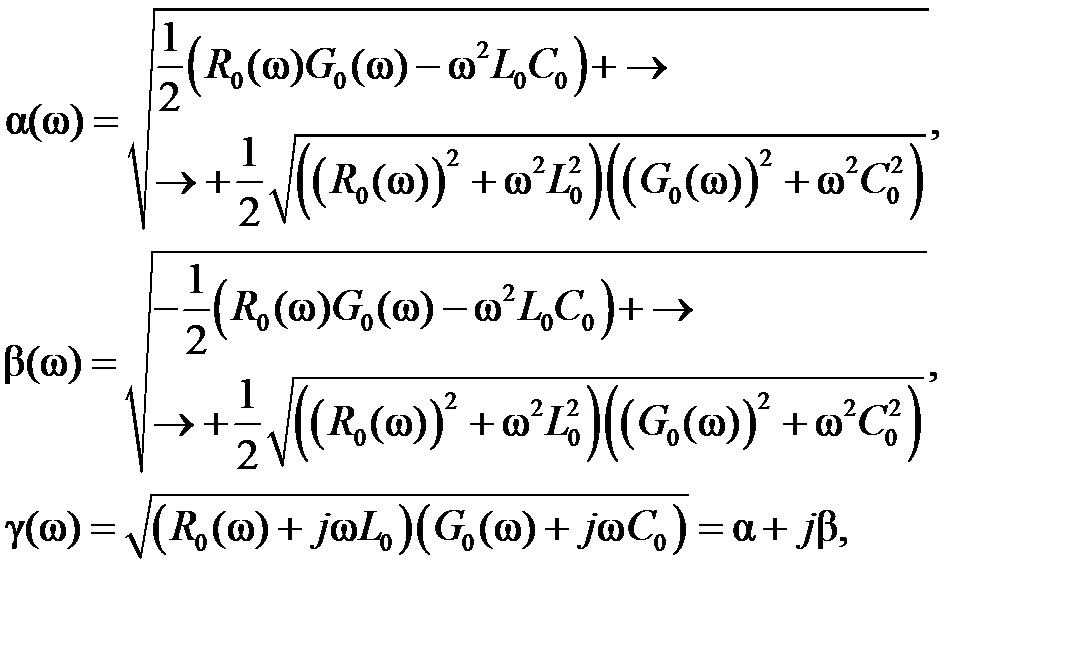
 (1.2.4)
(1.2.4)
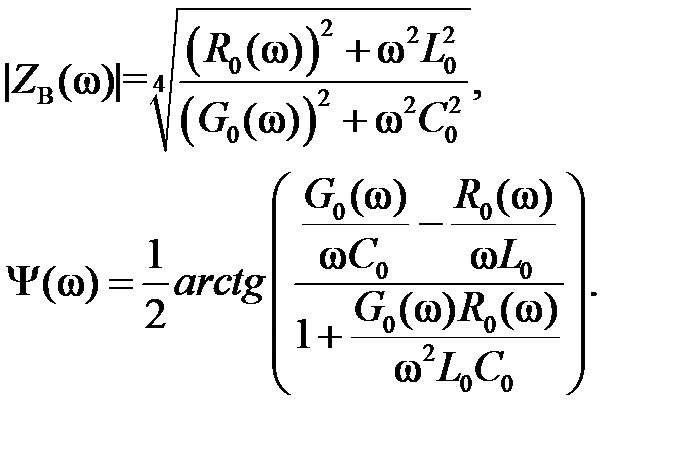 (1.2.5)
(1.2.5)
Основные термины и определения, применяемые при описании длинных линий, даны в ГОСТе [2, 5].
Пример расчета параметров линии в ППП Mathcad 15.
Перед прочтением данного параграфа рекомендуется ознакомиться с принципами расчетов в среде Mathcad 15 на основании литературы [1, 6].
Работа в ППП Mathcad 15 всегда начинается с ввода исходных данных.
При первом запуске программы необходимые команды для вычислений и математического моделирования могут отсутствовать. Поэтому пользователю следует сформировать удобный интерфейс для дальнейшей работы.
Во-первых, после создания нового файла, его, желательно, сразу же сохранить. Для этого лучше использовать английский текст во избежание ошибок чтения в других версиях программы.
При сохранении нужно указать путь и выбрать тип файла «XML-документ Mathcad (*xmcd)». При сохранении в более ранних версиях 13, 12 или 11, следует выбирать «XML-документ Mathcad v.13 (*xmcd)», «XML-документ Mathcad v.12 (*mcd)», «XML-документ Mathcad v.11 (*mcd)» соответственно.
Во-вторых, необходимо, вынести на рабочий экран используемые панели инструментов. Делается это с помощью команды «Вид» → «Панели инструментов» → «Математика». После ее появления в верхней левой части окна, можно щелкнуть левой кнопкой мыши на все пиктограммы  . В результате появятся панели инструментов, изображенные на рис. 1.2.1.
. В результате появятся панели инструментов, изображенные на рис. 1.2.1.
После этого на рабочем листе нужно ввести значения исходных параметров в соответствии с заданием на курсовую работу (см. табл. 2.1.1–2.1.3). Латинские обозначения вводятся обычным способом с клавиатуры на английской раскладке, а греческие – с панели «Греческий».
Для задания констант используется операция присваивания «:=» при помощи сочетания «Shift+:» или панели «Калькулятор».
Арифметические операции сложения, вычитания, умножения и деления вводятся нажатием клавиш «+», «-», «*», «/». Также это можно сделать при помощи панели «Калькулятор».
Функции квадратного корня или корня n-й степени, sin, cos, tg и т.д. также находятся на ней. Следует обратить внимание, что тангенс обозначается как tan, а арктангенс – atan.
Степень числа можно ввести командой «Shift+^», а число π – с панели «Греческий» (см. рис. 1.2.1)
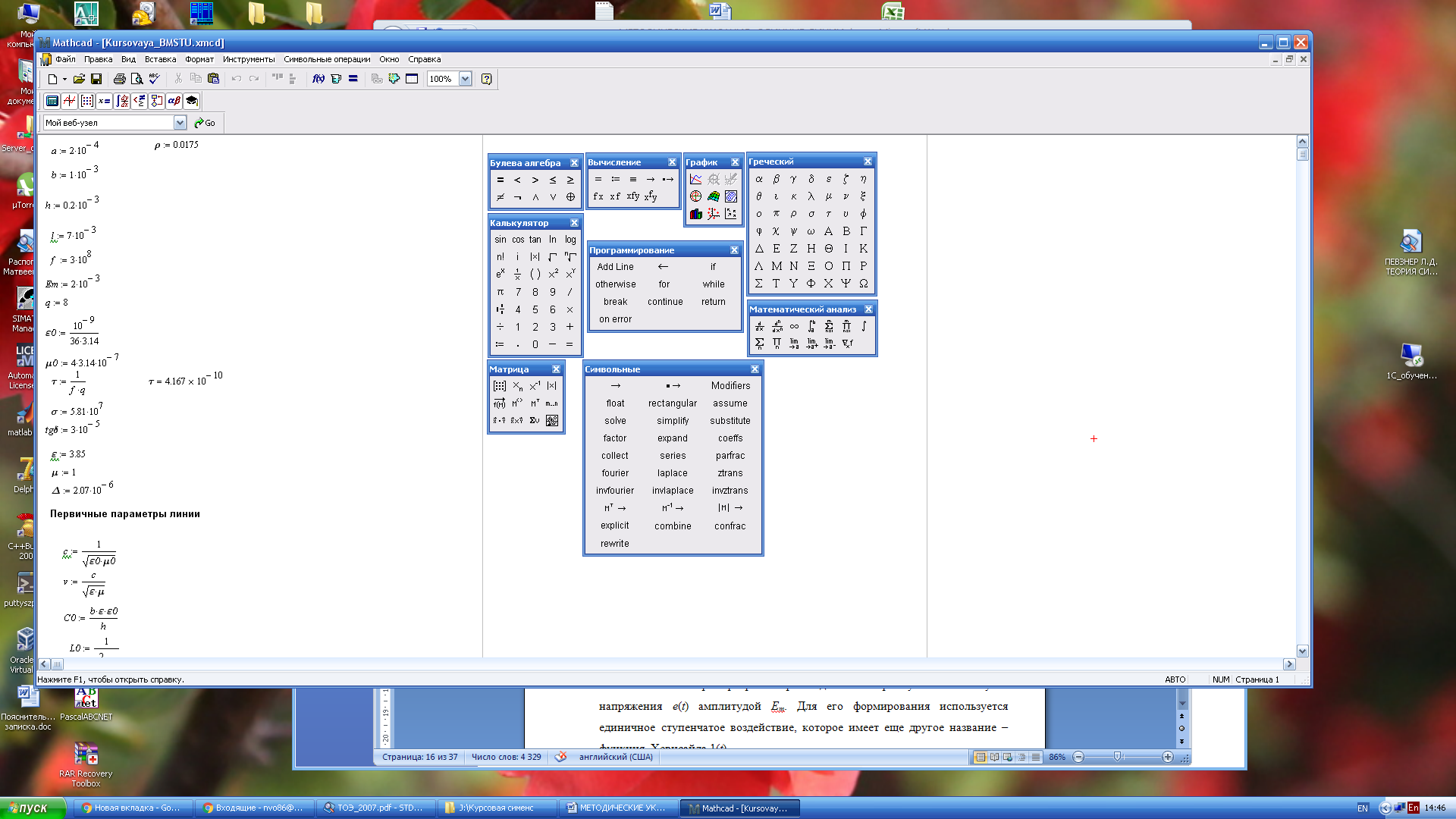
Рис 1.2.1. Рабочие панели инструментов Mathcad 15
Для вычисления какого-либо параметра требуется сначала написать формулу, по которой он определяется в соответствии с приведенными выше рекомендациями. В данном случае вместо знака «=» также используется знак присваивания «:=». А для вывода результата вычисления, необходимо осуществить ввод символа, обозначаемого величину, значение которой нужно вычислить, а затем нажать «=» на клавиатуре либо с панели «Калькулятор».
Мнимая единица обозначается как «1i» и автоматически преобразуется в «i».
Формула всегда должна располагаться на странице ниже данных, которые в нее входят, иначе символы выделяются красным цветом и переменная считается не определенной.
В Mathcad можно также добавлять подписи. Для этого следует на пустом поле начать вводить слова, и программа автоматически распознает их как текстовый формат. Для изменения формата текста, требуется щелкнуть по нему левой кнопкой мышки, выделить, а затем правой кнопкой выбрать подменю «Шрифт».
В качестве примера рассмотрим ввод исходных данных из задания: a, b, h, l, f, Em, q, ε0, μ0, ε, μ, σ, tgδ (рис. 1.2.2).
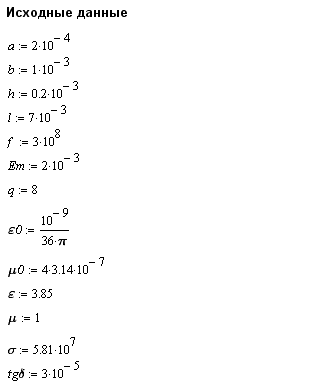
Рис 1.2.2. Пример ввода исходных данных в Mathcad 15
Теперь рассчитаем первичные и вторичные параметры длинной линии по формулам 1.2.1 – 1.2.5. Если параметр является функцией частоты ω, то она обязательно указывается в круглых скобках, например, R0(ω) (рис. 1.2.3).

Рис 1.2.3. Пример расчета первичных и вторичных параметров линии в Mathcad 15
Для построения графиков функций требуется нажать на пиктограмму  из панели «График». Затем на оси ординат вместо средней черной точки написать саму функцию с указанием в скобках параметра, от которого она зависит, а вместо крайних – нижний и верхний предел изменения функции, например, R0(ω) , диапазон: 0÷80. На оси абсцисс, где находится посередине черная точка, пишется аргумент ω, а там, где крайние точки – аналогично, как и на вертикальной оси – пределы его изменения, например, 0÷1011 (рис. 1.2.4).
из панели «График». Затем на оси ординат вместо средней черной точки написать саму функцию с указанием в скобках параметра, от которого она зависит, а вместо крайних – нижний и верхний предел изменения функции, например, R0(ω) , диапазон: 0÷80. На оси абсцисс, где находится посередине черная точка, пишется аргумент ω, а там, где крайние точки – аналогично, как и на вертикальной оси – пределы его изменения, например, 0÷1011 (рис. 1.2.4).

Рис 1.2.4. Ввод параметров на график
Чтобы график построился необходимо щелкнуть левой кнопкой мышки на пустое поле. Нажатие на область построения двойным щелчком приведет к открытию окна свойств под названием «Форматирование выбранного графика X-Y». На вкладке «Оси X,Y» для более точного вывода значений можно поставить галочку «сетка» на оси X и на основной оси Y. При помощи снятия галочки «Автосетка» и ввода значения в графу «количество сеток» меняется ее шаг.
Двойной щелчок мыши по закрашенному зеленому прямоугольнику, расположенному справа от надписи «Линии сетки» откроет окно «Цвет», где выбирается ее цвет. На вкладке «Трассировка», в пункте «Обозначение легенды», «Кривая 1», можно изменить тип линии, ее толщину и цвет. На вкладке «Подписи» можно ввести название заголовка и осей X и Y.
На рис. 1.2.5 – 1.2.10 показан пример построения первичных и вторичных параметров длинной линии, перечисленных ранее.
|
|
Рис 1.2.5. Зависимость погонного сопротивления от частоты

Рис 1.2.6. Зависимость погонной проводимости от частоты
|
|
Рис 1.2.7. Зависимость коэффициента ослабления от частоты
|
|
Рис 1.2.8. Зависимость коэффициента фазы от частоты
|
|
Рис 1.2.9. Зависимость волнового сопротивления от частоты
|
|
Рис 1.2.10. Зависимость фазы волнового сопротивления от частоты
Описание входных сигналов
Импульсный сигнал.
Импульсным сигналом называется сигнал напряжения или тока в цепи, отличный от нуля на конечном промежутке времени.
В качестве примера рассмотрим идеальный прямоугольный импульс напряжения e(t) амплитудой Em. Для его формирования используется единичное ступенчатое воздействие, у которого также есть другое название – функция Хевисайда 1(t).
Она имеет следующее описание:
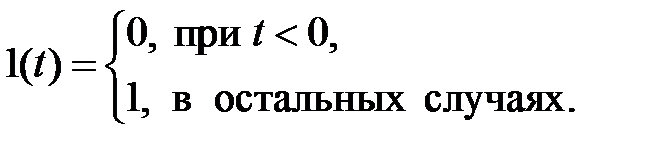 (1.3.1)
(1.3.1)
Существует и другое определение данной функции, отличающееся от предыдущего тем, что при t=0, 1(t) принимает значение, равное 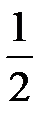 :
:
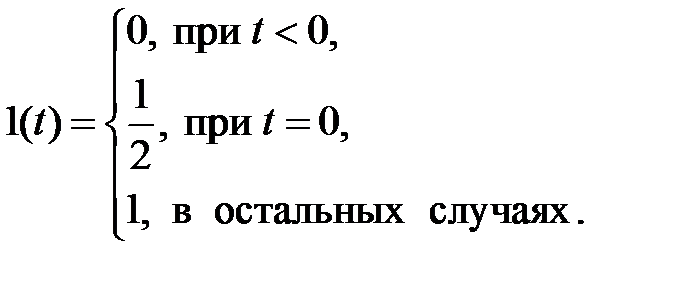 (1.3.2)
(1.3.2)
Сигнал 1(t), приходящий с задержкой на время τ, обозначается как 1(t - τ).
Окончательное описание входного импульсного сигнала e(t) получается из формулы:
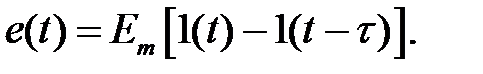 (1.3.3)
(1.3.3)
Для построения импульса, симметричного относительно нуля используется следующее выражение:
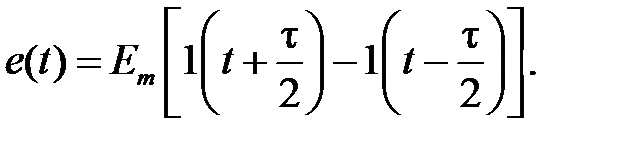 (1.3.4)
(1.3.4)
Способы формирования импульса e(t) согласно формулам (1.3.3) и (1.3.4) показаны на рис. 1.3.1. и рис. 1.3.2 соответственно.
| 1(t) |
| t |
| 0 |
| e(t) |
| t |
| t |
| 0 |
| τ |
| 0 |
| 1(t-τ) |
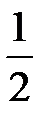
|
| Em |
Рис 1.3.1. Формирование идеального прямоугольного импульса
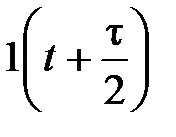
|
| t |
| 0 |
| e(t) |
| t |
| t |
| 0 |
| 0 |
| Em |

|
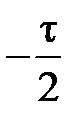
|
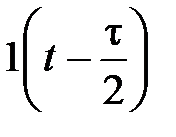
|
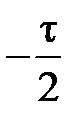
|

|
Рис 1.3.2. Формирование симметричного прямоугольного импульса
Функции можно также описывать, применяя разложение в тригонометрический ряд Фурье:
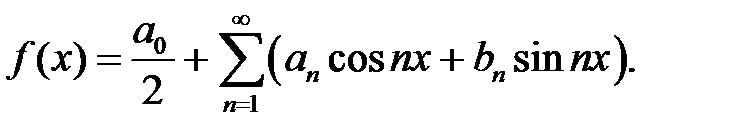 (1.3.5)
(1.3.5)
где коэффициенты ряда a0, an, bn вычисляются по формулам:

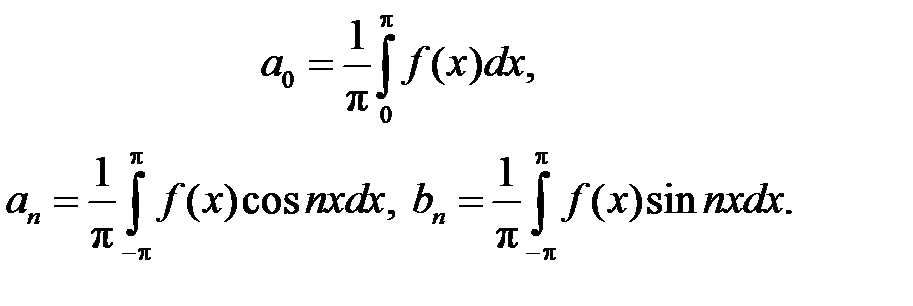 (1.3.6)
(1.3.6)
Заменяя в выражении (1.3.6) f(x) на Em, объединяя синусы и косинусы одной частоты, подставляя в (1.3.5) и заменяя предел суммы конечным пределом, получаем приближенное представление импульсного сигнала рядом Фурье:
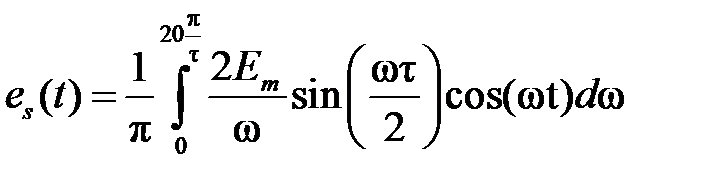 (1.3.7)
(1.3.7)
где τ – длительность импульса, определяемая из выражения:
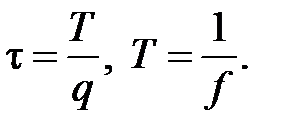 (1.3.8)
(1.3.8)
Переменная q представляет собой скважность и показывает во сколько раз период следования импульсов T превышает их длительность τ. Эти параметры используют для описания периодического сигнала, который будет рассмотрен далее.
Спектральная плотность сигнала представляет собой отношение сигнала на одной частоте на малом интервале времени к его ширине и может быть вычислена по формуле:
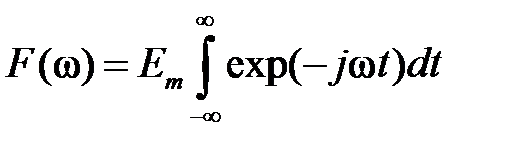 (1.3.9)
(1.3.9)
Это выражение носит название прямого преобразования Фурье.
Применяя обратное преобразование Фурье, можно восстановить импульсный сигнал как функцию времени:
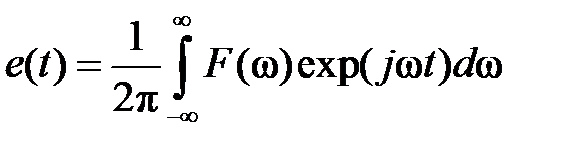 (1.3.10)
(1.3.10)
Пределы интегрирования в (1.3.9) и (1.3.10) обычно заменяют на конечные 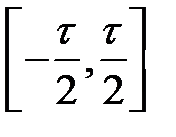 .
.
Периодический сигнал.
В качестве периодического сигнала будет рассматривать последовательность прямоугольных импульсов eT(t), имеющих период следования T, длительность τ и амплитуду Em (рис. 1.3.3).
| б) |
| 0 |
| t |
| 0 |
| Em |
| eT(t) |
| T |
| а) |
| Em |
| T |
| eT(t) |
| τ |
| τ |
| t |
Рис 1.3.3. Периодический сигнал а) нечетная функция, б) четная функция
Его упрощенное описание в виде последовательности двух импульсов имеет вид:
 (1.3.11)
(1.3.11)
Периодический сигнал имеет дискретное спектральное представление:

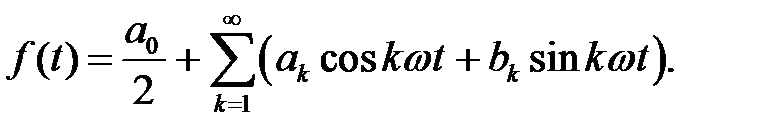 (1.3.12)
(1.3.12)
где k=1,2..∞, ω – частота основной гармоники.
Коэффициенты ряда a0, an, bn вычисляются по формулам:

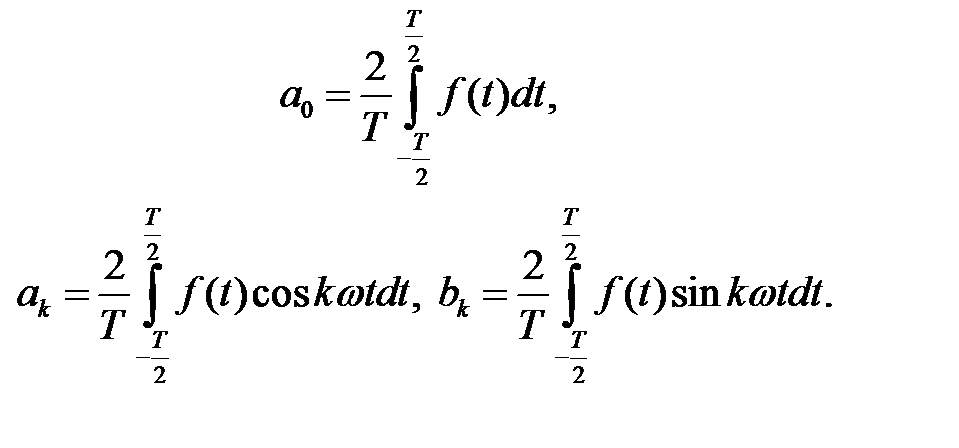 (1.3.13)
(1.3.13)
Если сигнал представляет собой нечетную функцию времени (рис. 1.3.3, а), то в тригонометрической записи ряда Фурье (1.3.12) остаются только синусоидальные составляющие bk. Для четной функции времени (рис. 1.3.3, б) в нуль обращаются коэффициенты bk, и ряд содержит только косинусоидальные составляющие ak.
Так, сигнал eT(t) из рис. 1.3.3, б при bk=0,  и f(t)=Em на интервале
и f(t)=Em на интервале 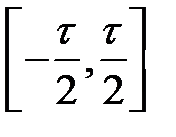 , согласно формулам (1.3.12) и (1.3.13) может быть представлен рядом Фурье:
, согласно формулам (1.3.12) и (1.3.13) может быть представлен рядом Фурье:

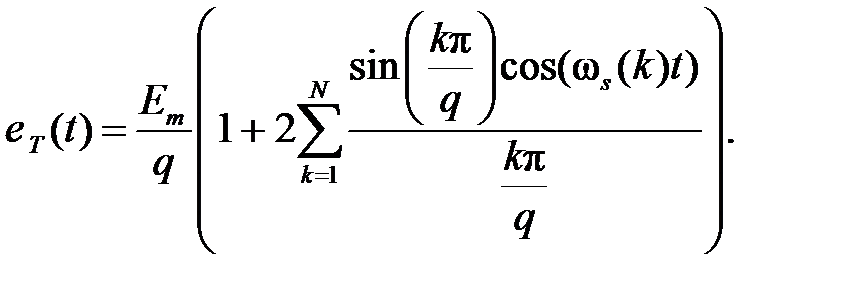 (1.3.14)
(1.3.14)
Здесь круговая частота изменяется дискретно 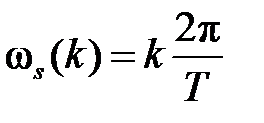 . Число гармоник N определяет точность приближения функции (1.3.14) к идеальной (см. рис. 1.3.3, б).
. Число гармоник N определяет точность приближения функции (1.3.14) к идеальной (см. рис. 1.3.3, б).
Пример составления модели сигналов в ППП Mathcad 15.
Для составления модели импульсного сигнала необходима функция Хевисайда. Алгоритм, описывающий единичный ступенчатый скачок Hev(t) согласно выражению (1.3.2) имеет следующую словесную формулировку: если t<0, то Hev(t)=0, иначе, если t=0, то Hev(t)= 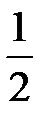 , иначе Hev(t)=1.
, иначе Hev(t)=1.
Для его реализации в Mathcad применяется панель инструментов «Программирование» с условным оператором «if», имеющий синтаксис if(условие 1, значение 1, if (условие 2, значение 2, значение3)). При этом условие 1 соответствует t<0, значение 1 – Hev(t)=0, условие 2 – t=0, значение 2 – Hev(t)= 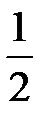 , значение 3 – Hev(t)=1.
, значение 3 – Hev(t)=1.
Прямоугольный импульс можно описать, используя обратное преобразование Фурье от его спектральной плотности (1.3.10).
В программе существует готовая команда, выполняющая его, на панели «Символьные» под названием «invfourier». При этом сначала пишется буквенное обозначение сигнала, затем знак присваивания, например «ee(t):=», а далее вызывается указанный оператор и слева от него, вместо черной точки вводится функция F(ω). Произойдет автоматическое преобразование, где символом Φ Mathcad обозначает функцию Хэвисайда. Результат отобразится после стрелки, стоящей справа от invfourier.
Для ввода интеграла при вычислении F(ω) и es(t) применяется панель «Математический анализ».
Пример вычисления параметров импульса, а также функций 1(t), e(t), es(t), T, τ, F(ω), по формулам (1.3.2 – 1.3.4, 1.3.7 – 1.3.10) приведен на рис. 1.3.4. При этом несимметричный импульс обозначен как e(t), симметричный – e _(t), полученный при помощи обратного преобразования Фурье – e __(t). Графики различных представлений импульсного сигнала показаны на рис. 1.3.5 – 1.3.8, а спектральная плотность – на рис. 1.3.9. Ее необходимо строить по модулю и в первой четверти.

Рис 1.3.4. Пример вычисления параметров импульсного сигнала
|
|
Рис 1.3.5. Несимметричный импульсный сигнал
|
|
Рис 1.3.6. Симметричный импульсный сигнал
|
|
Рис 1.3.7. Симметричный импульсный сигнал,
полученный при помощи обратного преобразования Фурье
|
|
Рис 1.3.8. Симметричный импульсный сигнал,
представленный разложением в ряд Фурье
|
|

Рис 1.3.9. Спектральная плотность импульсного сигнала
Теперь в качестве примера рассмотрим описание в Mathcad периодического сигнала (рис. 1.3.3, а). Здесь также может быть использован оператор «if», имеющий синтаксис if(условие 1, значение 1, if (условие 2, значение 2, if (условие 3, значение 3, if (условие 4, значение 4, значение 5)))). При этом условие 1 соответствует t<0, значение 1 – eT(t)=0, условие 2 – t<τ, значение 2 – eT(t)=Em, условие 3 – t<T, значение 3 – eT(t)=0, условие 4 – t<T+τ, значение 4 – eT(t)= Em, значение 5 – eT(t)= 0 согласно формуле (1.3.11).
Расчетные формулы для идеального периодического сигнала eT(t), ωs(k) и сигналов eTs 15(t), eTs 30(t), eTs 100(t), представленных разложением в ряд Фурье (1.3.14) для N=15, N=30 и N=100 гармоник соответственно приведены на рис. 1.3.10. При этом оператор суммы можно найти на панели «Математический анализ». Для построения нескольких характеристик на одном графике, необходимо выставить курсор справа от написанного параметра на оси ординат и нажать «,» на английской раскладке клавиатуры. Графики различного представления периодических сигналов показаны на рис. 1.3.11, 1.3.12. Из рис. 1.3.12 видно, что с увеличением N сигнал все сильнее приближается к идеальной последовательности импульсов.

Рис 1.3.10. Расчетные формулы для формирования периодического сигнала
|
|
Рис 1.3.11. Идеальный периодический сигнал
|
|
Рис 1.3.12. Периодический сигнал, представленный разложением в ряд Фурье
Описание выходных сигналов
Пример расчета реакции системы в ППП Mathcad 15.
Для исследования переходных процессов, отражающих реакцию на идеальный периодический сигнал используем выражения (1.4.4) – (1.4.9), а на приближенный – (1.4.10), (1.4.11).
Обратное преобразование Лапласа осуществляется в программе при помощи команды на панели «Символьные» под названием «inv laplace». Cначала пишется буквенное обозначение сигнала, затем знак присваивания, например «UL 1(t):=», а далее вызывается указанный оператор и слева от него, вместо черной точки вводится функция U1(s). Произойдет автоматическое преобразование. Результат отобразится после стрелки, стоящей справа от inv laplace.
По умолчанию Mathcad оставляет большое количество знаков после запятой, и при таких расчетах решение отображается зачастую на нескольких страницах. Для обеспечения более компактного отображения следует выполнить некоторую последовательность действий: поставить курсор на какое-нибудь числовое значение в вычисленном выражении после стрелки, далее нажать в меню «Формат»→»Результат». На вкладке «Формат числа» выбрать «Дробь», установить уровень точности, например, 3, поставить галочку напротив фразы «Применять в символьных результатах». Также на данной вкладке можно выбрать форматы «Научный» или «Инженерный» и отметить флаг «Показатели степени в виде E±000».
Пример расчета параметров реакции на импульсный сигнал приведен на рис. 1.4.2.

Рис. 1.4.2. Расчет параметров реакции на импульсный сигнал
Зависимость модуля коэффициента усиления от частоты |Ku(ω)| показана на рис. 1.4.3, откуда следует, что на частоте ω<108 рад/с он достаточно близок к 1. Поэтому установившееся значение реакции системы будет мало отличаться от амплитуды входного импульса.
В области частот ω>108 рад/с коэффициент усиления начинает резко снижаться (рис. 1.4.4).
Графики реакций системы us(t), h(t)=UL 1(t)-UL 2(t) на импульсные сигналы e(t), es(t) приведены на рис. 1.4.5, 1.4.6. Число гармоник N взято равным 15.
|
|
Рис. 1.4.3. Коэффициент усиления длинной линии на частоте ω<108 рад/с
|
|
Рис. 1.4.4. Коэффициент усиления длинной линии на частоте ω>108 рад/с
|
|
Рис. 1.4.5. Реакция системы на идеальный импульсный сигнал.
|
|
Рис. 1.4.6. Реакция системы на импульсный сигнал, представленный разложением в ряд Фурье при N=15.
Для расчета реакции на периодический сигнал удобно сначала найти преобразование Лапласа от функций h1(t) и h2(t), а затем построить переходную характеристику eLt(t) согласно условию (1.4.14), а uTs(t) – согласно (1.4.15). Пример ее вычисления показан на рис. 1.4.7. Графики реакций системы на указанные периодические сигналы приведены на рис. 1.4.8, 1.4.9. Число гармоник N также равно 15.

Рис. 1.4.7. Расчет параметров реакции на импульсный сигнал
|
|
 Рис. 1.4.8. Реакция системы на идеальный периодический сигнал.
Рис. 1.4.8. Реакция системы на идеальный периодический сигнал.
|
|
Рис. 1.4.9. Реакция системы на периодический сигнал, представленный разложением в ряд Фурье при N=15.
Пример расчета частотных характеристик в ППП Mathcad 15.
Произведем расчет частотных характеристик длинной линии. В качестве примера возьмем ситуацию, когда на ее вход подается ступенчатый сигнал Em·1(t). Его изображение по Лапласу имеет вид:
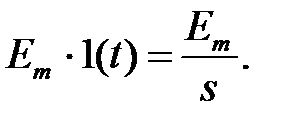 (1.5.7)
(1.5.7)
Умножая правую часть на Ku(s) и, заменяя s=jω, получим частотную характеристику:
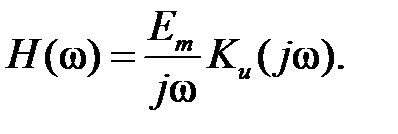 (1.5.8)
(1.5.8)
В Mathcad можно получить выражение (1.5.8) в параметрическом виде как функцию частоты. Для этого применяется оператор «simplify» из панели «Символьные». Аналогично преобразованию Лапласа (см. пункт 1.4), сначала вводится выражение «H(ω):=», затем вместо черного прямоугольника заносится правая часть выражения (1.5.8). Вычисления происходит автоматически (рис. 1.5.1). Сокращение количества знаков после запятой можно выполнить с применением меню «Формат»→«Результат» (см. пункт 1.4).
Проверку правильности построения указанных характеристик можно проверить как графическим, так и аналитическим способами. При этом точка их перегиба обязательно должна находиться при частоте 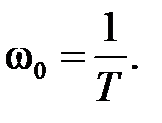 Найти ее можно в выражении UL1(t) в степени экспоненты и без знака «-» (см. рис. 1.4.2). В нашем примере эта точка равна ω0=21.865E+009.
Найти ее можно в выражении UL1(t) в степени экспоненты и без знака «-» (см. рис. 1.4.2). В нашем примере эта точка равна ω0=21.865E+009.
Для нахождения точки перегиба аналитически заменим аргумент ω на x в целях того, чтобы отличать два способа. Напишем две функции |A1(x)| =|H(x)| и |A2(x)| =|H(21.865E+009)| – для АЧХ, |F1(x)| = arg(H(x)) и |F2(x)| =arg(H(21.865E+009)) – для ФЧХ. Условием пересечения данных графиков является равенство нулю их разности:
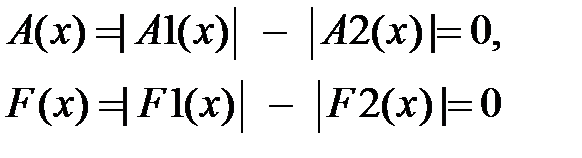 (1.5.9)
(1.5.9)
Решая уравнения (1.5.9) относительно x, получают точку перегиба. Для нахождения корней уравнения x может быть применена функция ωA=root(A(x),x) – для АЧХ и ωF=root(F(x),x). Вместо x необходимо задавать начальное приближение, близкое к числу 21.865E+009. Например, 21·109.
Из результатов вычисления (рис. 1.5.1) видно, что найденные решения практически совпадают с точкой ω0: ωA=2,187·1010≈21.865E+009, ωF=2,186·1010≈21.865E+009.

Рис 1.5.1. Пример расчета частотной характеристики длинной линии
Для построения АЧХ требуется записать на оси ординат модуль характеристики |H(ω)|, а ФЧХ – ее аргумент arg(H(ω)). Их удобно представлять в логарифмическом масштабе. Для этого в свойствах графика необходимо поставить галочку напротив «Логарифмический масштаб» под надписью «Ось X» и «Основная ось Y».
 Лучше построить сразу на одном графике модуль |H(ω)| и его значение в зависимости от найденной точки |H(ω0)| =|H(21.865E+009)|. Понятно, что последняя характеристика будет представлять из себя прямую, параллельную оси абсцисс (рис. 1.5.2). Аналогично строятся два графика для ФЧХ arg(H(ω)) и arg(H(21.865E+009)) (рис. 1.5.3).
Лучше построить сразу на одном графике модуль |H(ω)| и его значение в зависимости от найденной точки |H(ω0)| =|H(21.865E+009)|. Понятно, что последняя характеристика будет представлять из себя прямую, параллельную оси абсцисс (рис. 1.5.2). Аналогично строятся два графика для ФЧХ arg(H(ω)) и arg(H(21.865E+009)) (рис. 1.5.3).
 Рис 1.5.2. Амплитудно-частотная характеристика длинной линии
Рис 1.5.2. Амплитудно-частотная характеристика длинной линии
Рис 1.5.3. Фазочастотная характеристика длинной линии
Оценка искажений сигналов
Оценка искажений представляет отклонение выходного сигнала от входного. Для идеального импульсного сигнала оно вычисляется по формуле:
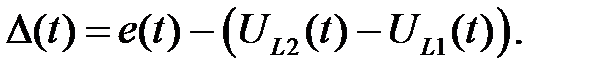 (1.6.1)
(1.6.1)
Для того же сигнала, представленного разложением в ряд Фурье:
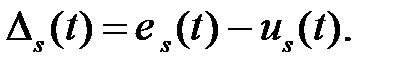 (1.6.2)
(1.6.2)
Для идеального периодического сигнала:
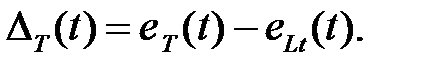 (1.6.3)
(1.6.3)
Для периодического сигнала, представленного разложением в ряд Фурье:
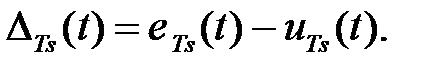 (1.6.4)
(1.6.4)
Пример расчета искажений сигналов в ППП Mathcad 15.
Для расчета искажений импульсного Δ(t) и периодического идеальных ΔT(t) сигналов и тех же сигналов, представленных в виде ряда Фурье Δs(t) и ΔTs(t) применимы формулы (1.6.1 – 1.6.4).
Пример вычислений приведен на рис 1.6.1, а на рис. 1.6.2 – 1.6.5 показаны временные диаграммы отклонений. Индекс функции eTs15(t) означает, что число гармоник равно 15.

Рис. 1.6.1. Пример расчета искажений сигналов
|
|
Рис. 1.6.2. Отклонение выходного сигнала относительно идеального входного импульсного сигнала
|
|
Рис. 1.6.3. Отклонение выходного сигнала относительно идеального входного периодического сигнала

Рис. 1.6.4. Отклонение выходного сигнала относительно входного импульсного сигнала, представленного разложением в ряд Фурье.
|
|
Рис. 1.6.5. Отклонение выходного сигнала относительно входного периодического сигнала, представленного разложением в ряд Фурье.
Требования к курсовой работе
Примеры заданий на курсовую работу
Примерные варианты заданий на курсовую работу приведены в табл. 2.1.1, параметры высокочастотных материалов – в табл. 2.1.2, электропроводность некоторых металлов – в табл. 2.1.3.
Тема курсовой работы: «Исследование однородной линии передачи с распределенными параметрами».
Задание: произвести анализ и расчет электротехнического устройства с использованием линий с распределенными параметрами:
- толщина полоскового проводника, a, мм;
- ширина полоскового проводника, b, мм;
- высота слоя диэлектрика, h, мм;
- длина элементарного участка линии, l, мм;
- частота импульса f, МГц;
- амплитуда импульса, Е m, мВ;
- скважность периодического сигнала, q.
Таблица 2.1.1 Примерные варианты заданий на курсовую работу
| № вар. | a | b | h | l | Диэлектрик | Металл | f | Е m | q |
| 1. | 0,27 | 1,1 | 0,21 | 7 | полиэтилен | серебро | 500 | 2 | 8 |
| 2. | 0,3 | 1,2 | 0,22 | 6 | полистирол | серебро | 510 | 2 | 3 |
| 3. | 0,22 | 0,9 | 0,23 | 5 | фторопласт | серебро | 520 | 2 | 4 |
| 4. | 0,25 | 1,0 | 0,20 | 6 | плексиглас | серебро | 530 | 2 | 5 |
| 5. | 0,27 | 1,1 | 0,21 | 7 | плавленый кварц | серебро | 490 | 2 | 6 |
| 6. | 0,25 | 1,0 | 0,20 | 7 | полиэтилен | медь | 500 | 1 | 3 |
| 7. | 0,27 | 1,1 | 0,21 | 6 | полистирол | медь | 510 | 1 | 4 |
| 8. | 0,3 | 1,2 | 0,22 | 5 | фторопласт | медь | 520 | 1 | 5 |
| 9. | 0,22 | 0,9 | 0,23 | 6 | плексиглас | медь | 530 | 1 | 6 |
| 10. | 0,25 | 1,0 | 0,20 | 7 | плавленый кварц | медь | 490 | 1 | 7 |
| 11. | 0,22 | 0,9 | 0,23 | 7 | полиэтилен | цинк | 500 | 1 | 6 |
| 12. | 0,25 | 1,0 | 0,20 | 6 | полистирол | цинк | 510 | 2 | 7 |
| 13. | 0,27 | 1,1 | 0,21 | 5 | фторопласт | цинк | 520 | 2 | 8 |
| 14. | 0,3 | 1,2 | 0,22 | 6 | плексиглас | цинк | 530 | 2 | 3 |
| 15. | 0,22 | 0,9 | 0,23 | 7 | плавленый кварц | цинк | 490 | 2 | 4 |
| 16. | 0,25 | 1,0 | 0,20 | 7 | полиэтилен | серебро | 500 | 2 | 5 |
| 17. | 0,27 | 1,1 | 0,21 | 6 | полистирол | серебро | 500 | 2 | 6 |
| 18. | 0,3 | 1,2 | 0,22 | 5 | фторопласт | серебро | 510 | 1 | 7 |
| 19. | 0,22 | 0,9 | 0,23 | 6 | плексиглас | серебро | 520 | 1 | 8 |
| 20. | 0,25 | 1,0 | 0,20 | 7 | плавленый кварц | серебро | 530 | 1 | 3 |
| 21. | 0,3 | 1,2 | 0,22 | 7 | полиэтилен | латунь | 500 | 2 | 7 |
| 22. | 0,22 | 0,9 | 0,23 | 6 | полистирол | латунь | 510 | 1 | 8 |
| 23. | 0,25 | 1,0 | 0,20 | 5 | фторопласт | латунь | 520 | 1 | 3 |
| 24. | 0,27 | 1,1 | 0,21 | 6 | плексиглас | латунь | 530 | 1 | 4 |
| 25. | 0,3 | 1,2 | 0,22 | 7 | плавленый кварц | латунь | 490 | 1 | 5 |
Таблица 2.1.2 Параметры высокочастотных материалов
| Материал | Относительная диэлектрическая проницаемость | Тангенс угла потерь на частоте 1 ГГц |
| Полиэтилен | 2,25 | 2·10-4 |
| Полистирол | 2,56 | 2·10-4 |
| Фторопласт | 2,08 | 2,5·10-4 |
| Плавленный кварц | 3,85 | 3·10-5 |
| Плексиглакс | 3,40 | 2·10-3 |
Таблица 2.1.3 Электропроводность некоторых металлов
| Металл | Удельная объемная проводимость, См/м |
| Серебро | 6,17·107 |
| Медь | 5,81·107 |
| Цинк | 1,69·107 |
| Латунь | 1,55·107 |
Требования к выполнению курсовой работы
В курсовой работе обязательным является выполнение графической части на листах формата А4, на которых должны быть вычерчены:
1. Чертеж длинной линии;
2. Эквивалентная схема звена длинной линии;
3. Графики изменения первичных и вторичных параметров длинной линии;
4. Графики переходных процессов в длинной линии.
Курсовая работа должна в краткой и четкой форме раскрывать творческий замысел работы, при необходимости сопровождаться схемами, иллюстрациями и т.п., содержать методы исследования, методику расчетов и моделирования.
Общими требованиями к оформлению курсовой работы являются:
1) обоснованность рекомендаций и предложений;
2) убежденность аргументации;
3) краткость и точность формулировок;
4) корректность изложения результатов работы;
5) четкость и логическая последовательность изложенного материала.
Курсовая работа сдается в печатном виде.
Номер варианта задания курсовой работы определяется номером записи фамилии студента в журнале преподавателя.
2.3 Требования к оформлению курсовой работы
Курсовую оформляют в соответствии с ГОСТ 2.105-79 [4] на страницах формата А4, текст печатается на компьютере, гарнитурой Times New Roman, шрифт не менее 12, через 1,5 интервала, с выравниванием по ширине. Расчетно-пояснительная записка и задание оформляются в соответствие с приложениями Б и В.
Страницы нумеруются арабскими цифрами. В общую нумерацию входят все листы. На расчетно-пояснительной записке и задании номера страниц не ставятся.
Число иллюстраций должно быть достаточным для пояснения излагаемого текста. Нумерация страниц ставится сквозная, рисунки в пределах раздела. Например, рис. 1.1, 1.2 соответствует первой части работы, рис. 2.1, 2.2 — второй и т.д. Рисунок помещается после первого упоминания в тексте.
Таблицы в тексте могут иметь заголовки, их нумеруют в пределах раздела. На все таблицы и рисунки, помещенные в тексте курсовой работы, необходимо указывать ссылки.
Ссылки должны быть и на использованную литературу, перечень которой приводится в последней части, с указанием названия учебника или учебного пособия, фамилии и инициалов авторов, издательства и года издания.
Содержание дается на отдельном листе и помещено перед индивидуальным заданием. Наименование разделов и подразделов приводят с указанием номеров страниц, на которых размещается их начало.
Схема замещения длинной линии выполняется с соблюдением необходимых требований ЕСКД и ГОСТов [3].
Требования к защите и оценке курсовой работы
Для защиты курсовой работы требуется сдать 4 модуля, описание которых дано во введении, оформить ее в печатном виде в соответствии с требованиями, изложенными в пунктах 2.2 и 2.3.
Модуль считается выполненным, если студент получил за него оценку в баллах, не ниже минимальной (см. табл. П.1).
Студенты, не сдавшие модуль в установленный срок, продолжают работать над ним в соответствие с порядком, принятым кафедрой.
Шкала перевода рейтинговых оценок по всем модулям в оценку на зачете представлена в табл. П.3.
3. Контрольные вопросы к защите курсовой работы
Модуль №1
1.Что такое полосковая линия передачи?
2.Каковы первичные параметры длинной линии?
3.Начертить эквивалентную схему элементарного участка длинной линии.
4.Что такое погонные реактивные параметры?
5.От чего зависят погонные параметры омических потерь?
Модуль №2
1. Что такое импульсный сигнал?
2. Как определить выходной сигнал четырехполюсника с помощью преобразования Фурье?
3. Что такое спектральная плотность выходного сигнала?
4. Зачем применяется преобразование Лапласа?
5. Как определить изображение выходного сигнала по Лапласу?
Модуль №3
1. Поясните формулу для описания входного импульсного сигнала?
2. Поясните формулу для описания выходного спектрального сигнала?
3. Как вычислить отклонение входного сигнала от выходного?
4. Что такое периодический входной сигнал?
5. Как определяется передаточная функция длинной линии?
Модуль №4
1. Дайте оценку искажений сигналов при их передаче в линии.
2. Проанализируйте факторы, вызывающие искажения сигналов.
3. Дайте пояснения частотным зависимостям вторичных параметров линии.
4. В чем отличие передаточной функции длинной линии от передаточной функции сосредоточенного четырехполюсника?
5. Какова роль согласованной нагрузки?
Заключение
В результате выполнения курсовой работы студенты получат следующие социально-личностные компетенции (СОК) и собственные общепрофессиональные компетенции (СОПК):
СОК-6 – способность работать в команде, толерантно воспринимая социальные и культурные различия.
СОК-7 – способность к самоорганизации и самообразованию.
СОК-10 – способность выстраивать логику рассуждений и высказываний, проводить анализ, систематизацию, классификацию, интерпретацию соответствующей информации, формулировать выводы, адекватные полученным результатам.
СОК-11 – владение способами приобретения и извлечения знаний, осуществления самостоятельной учебно-познавательной деятельности, выбора наиболее эффективных способов и алгоритмов решения задач в зависимости от конкретных условий.
СОК-13 – способность к самостоятельному выбору способа решения проблемы из альтернативных вариантов на основе выявления и устранения противоречий в системе.
СОК-14 – способность решать нестандартные задачи, в том числе за пределами профессионального поля деятельности.
СОПК-2 – способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования.
СОПК-5 – способность использовать современные компьютерные технологии поиска информации для решения поставленной задачи, критического анализа этой информации и обоснования принятых идей и подходов к решению.
Также студент будет знать:
- понятия: линия с распределенными параметрами, линия с сосредоточенными параметрами, погонная емкость, погонная индуктивность, погонное сопротивление потерь, тангенс угла потерь, волновое сопротивление, скважность периодического сигнала, комплексная спектральная плотность, комплексный спектр сигнала.
-=методики анализа и расчета электротехнических устройств с использованием линий с распределенными параметрами, работы со справочной литературой и программным обеспечением.
- программное обеспечение Mathcad 15.
Список литературы
1. Алексеев Е.Р., Чеснокова О.В. Основы работы в математическом пакете MathCAD. – Из-во: ДонНТУ, 2012. –187c.
2. ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения.
3. ГОСТ 2.702-2011. Правила выполнения электрических схем
4. ГОСТ 7.32-2001. «Отчёт о научно-исследовательской работе». Структура и правила оформления.
5. ГОСТ 21702-76. Устройства СВЧ. Полосковые линии.
6. Макаров Е. Инженерные расчеты в Mathcad 15. – СПб.: Питер, 2011. –400 c.
7. Николаев С.С., Судаков В.Ф. Анализ и расчет электротехнических устройств с использованием линий с распределенными параметрами: Учеб. пособие/Под ред. С.И. Масленниковой. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 24 с.: ил.
Приложения
Приложение А. Система контроля знаний студентов
Таблица П.1 Рейтинговая система контроля освоения дисциплины
| Неделя проведения контроля модуля | Оценка за модуль в баллах | ||
| Максимальная | Минимальная | ||
| Модуль 1 | 4 | 25 | 15 |
| Модуль 2 | 7 | 25 | 15 |
| Модуль 3 | 10 | 25 | 15 |
| Модуль 4 | 14 | 25 | 15 |
| Итоговый рейтинг | 100 | 60 | |
Таблица П.2 Шкала перевода в рейтинговую оценку
Модуль 1
Модуль 2
Модуль 3
Модуль 4
Таблица П.3 Шкала перевода рейтинговых оценок по всем видам занятий и самостоятельной работы в зачет по дисциплине*
| Рейтинг | Оценка на зачете |
| 85 – 100 | отлично |
| 73 - 84 | хорошо |
| 60 – 72 | удовлетворительно |
| 0 – 59 | неудовлетворительно |
*У студентов существует возможность повысить свой рейтинг и получить баллы за проявление личностных качеств: трудовая дисциплина, ответственность, инициатива и др. Максимальный балл – 10, минимальный – 0. Начисление баллов за личностные качества осуществляется преподавателями, как в процессе обучения, так и при подведении итогов по дисциплине. Эти баллы суммируются с баллами, полученными за все модули по дисциплине.
Приложение Б. Пример расчетно-пояснительной записки
Приложение В. Пример листа с заданием на курсовую работу 
Н.В. Осипова
Исследование однородной линии передачи с распределенными параметрами
Электронное учебное издание
Методические указания к курсовой работе
по дисциплине «Электротехника»
Москва
УДК 621.3.011.711
УДК 621.3.011.715
УДК 621.3.012.6 — 621.3.012.8
Рецензент:
Осипова Н. В.
Исследование однородной линии передачи с распределенными параметрами. Электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2016. 60 с.
Представлены основные теоретические сведения об однородных электрических цепях с распределенными параметрами. Приведены примеры расчета и математического моделирования электротехнического устройства с использованием длинной линии в пакете прикладных программ MathCad 15.
Для студентов МГТУ имени Н.Э. Баумана, обучающихся по специальности "Информационные системы и технологии".
Рекомендовано учебно-методической комиссией факультета «Информатика и системы управления» МГТУ им. Н.Э. Баумана
Электронное учебное издание
Осипова Нина Витальевна
Дата: 2019-03-05, просмотров: 431.


















