Первичные параметры линии.
К первичным параметрам длинной линии относятся:
- погонная емкость С0=С dl, Ф/м;
- погонная индуктивность L0=Ldl, Гн/м;
- погонное сопротивление R0=Rdl, Ом/м;
- погонная проводимость G0=Gdl, См/м;
Для их вычисления необходимо иметь следующие исходные данные:
- относительная диэлектрическая проницаемость (безразмерная) ε.
- диэлектрическая проницаемость вакуума (электрическая постоянная) ε0, Ф/м.
- относительная магнитная проницаемость (безразмерная) μ.
- магнитная проницаемость вакуума (магнитная постоянная) μ0, Гн/м.
- частота следования периодического сигнала f, Гц.
- удельная объемная проводимость вещества σ, См/м.
- тангенс потерь – tgδ, а также a, b, h, dl, о которых было сказано ранее.
Дадим краткое определение перечисленным параметрам.
С0 характеризует способность проводника элементарной длины dl накапливать электрический заряд.
В индуктивности L0 запасается энергия магнитного поля на малом участке dl.
R0 определяет способность проводника элементарной длины dl препятствовать прохождению тока через него.
G0 характеризует величину, обратную сопротивлению, но за единицу измерения чаще всего принимается не 1/(Ом·м), а См/м (сименс на метр).
Параметр ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме.
Электрическая постоянная ε0 в системе СИ приближенно равна ε0 ≈ 8,85·10−12 Ф/м.
Значение μ показывает, во сколько раз магнитная индукция в веществе больше, чем в воздухе или вакууме.
Численное значение магнитной постоянной μ0≈ 4π·10−7 Гн/м.
Параметр f характеризует число импульсов сигнала, поступающих на вход линии за единицу времени.
Удельная объемная проводимость вещества σ определяет способность проводить электрический ток на единицу длины.
Параметр tgδ используется для оценки способности диэлектрика рассеивать энергию в электрическом поле, т.е. показывает, каковы ее потери.
Расчеты первичных параметров линии будет осуществлять согласно методике [7].
По заданным значениям ε, μ и известным ε , μ0 можно найти скорость света в вакууме c и в диэлектрике (фазовую скорость) v.
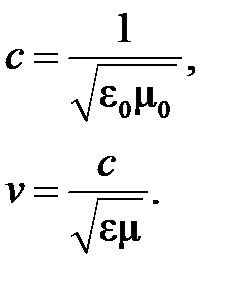 (1.2.1)
(1.2.1)
По геометрическим параметрам b, h определяют погонные реактивные параметры C0 и L0:
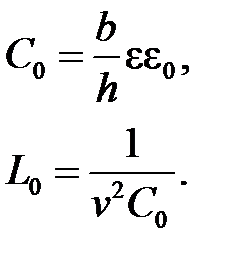 (1.2.2)
(1.2.2)
Погонные параметры омических потерь R0 и G0 являются функциями круговой частоты ω:
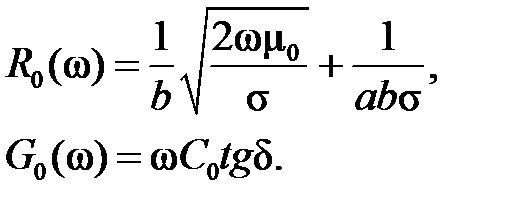 (1.2.3)
(1.2.3)
Вторичные параметры линии.
К вторичным параметрам длинной линии относятся:
- коэффициент распространения γ, 1/м;
- коэффициент ослабления – α, Нп/м;
- коэффициент фазы – β, рад/м;
- модуль волнового сопротивления, |Zв|, Ом;
- фаза волнового сопротивления, Ψ, рад.
Коэффициент распространения γ показывает изменение величины напряжения бегущей волны и его фазовый сдвиг на единицу длины линии.
Коэффициент ослабления α показывает, во сколько раз выходная мощность сигнала в схеме меньше входной (в данном случае на участке dl). Измеряется обычно в дБ, но применяется также и величина, называемая Непером (1 Нп=8,685889638 дБ).
Коэффициент фазы (фазовая постоянная) β характеризует изменение угла вектора тока или напряжения на участке линии элементарной длины dl.
Волновое сопротивление длинной линии Zв определяется отношением амплитуды напряжения падающей, отраженной или бегущей волны к амплитуде силы тока той же волны. При расчетах используется только модуль данной величины |Zв|.
Фаза волнового сопротивления Ψ характеризует разность фаз волн напряжения и тока.
Для их вычисления необходимо иметь зависимости C0, L0, R0(ω) и G0(ω), найденные на предыдущем этапе, следовательно, параметры γ, α, Zв, Ψ также будут являться функциями круговой частоты ω [7]:
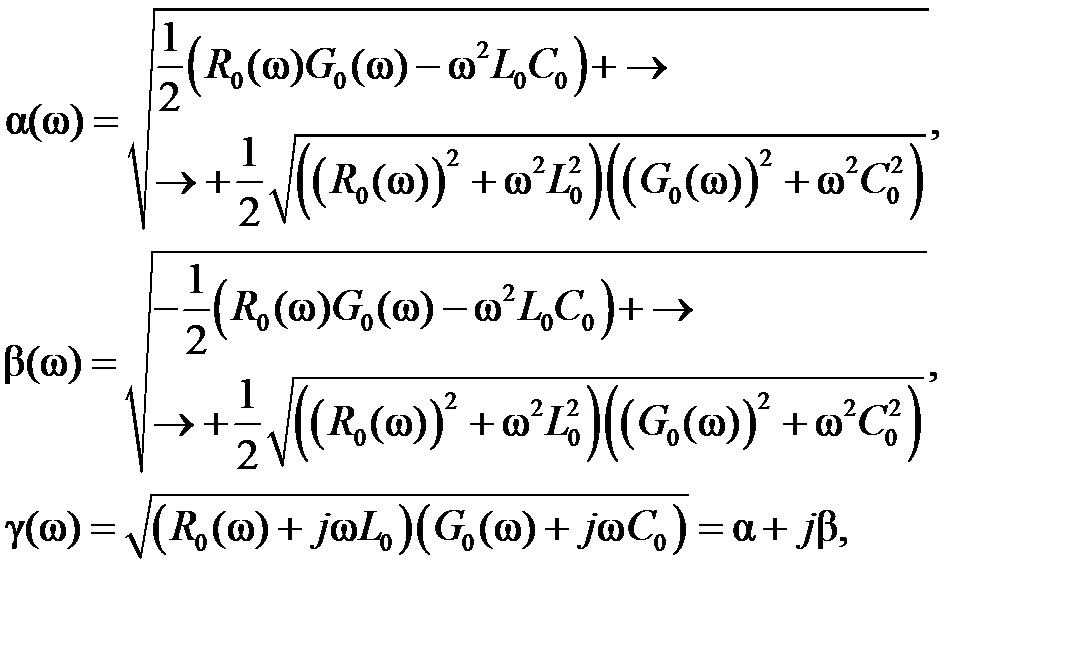
 (1.2.4)
(1.2.4)
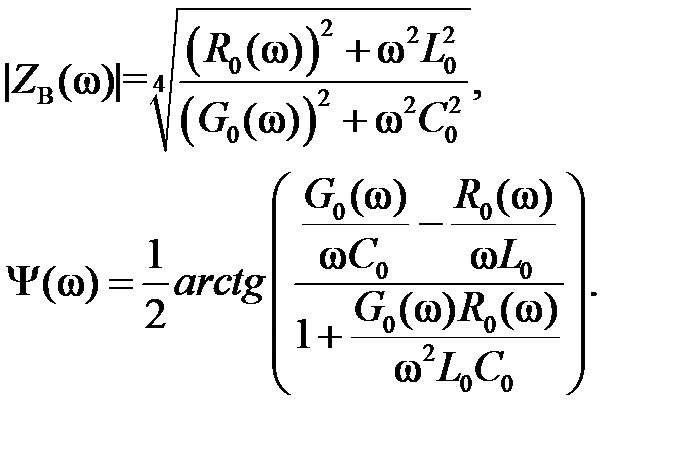 (1.2.5)
(1.2.5)
Основные термины и определения, применяемые при описании длинных линий, даны в ГОСТе [2, 5].
Пример расчета параметров линии в ППП Mathcad 15.
Перед прочтением данного параграфа рекомендуется ознакомиться с принципами расчетов в среде Mathcad 15 на основании литературы [1, 6].
Работа в ППП Mathcad 15 всегда начинается с ввода исходных данных.
При первом запуске программы необходимые команды для вычислений и математического моделирования могут отсутствовать. Поэтому пользователю следует сформировать удобный интерфейс для дальнейшей работы.
Во-первых, после создания нового файла, его, желательно, сразу же сохранить. Для этого лучше использовать английский текст во избежание ошибок чтения в других версиях программы.
При сохранении нужно указать путь и выбрать тип файла «XML-документ Mathcad (*xmcd)». При сохранении в более ранних версиях 13, 12 или 11, следует выбирать «XML-документ Mathcad v.13 (*xmcd)», «XML-документ Mathcad v.12 (*mcd)», «XML-документ Mathcad v.11 (*mcd)» соответственно.
Во-вторых, необходимо, вынести на рабочий экран используемые панели инструментов. Делается это с помощью команды «Вид» → «Панели инструментов» → «Математика». После ее появления в верхней левой части окна, можно щелкнуть левой кнопкой мыши на все пиктограммы  . В результате появятся панели инструментов, изображенные на рис. 1.2.1.
. В результате появятся панели инструментов, изображенные на рис. 1.2.1.
После этого на рабочем листе нужно ввести значения исходных параметров в соответствии с заданием на курсовую работу (см. табл. 2.1.1–2.1.3). Латинские обозначения вводятся обычным способом с клавиатуры на английской раскладке, а греческие – с панели «Греческий».
Для задания констант используется операция присваивания «:=» при помощи сочетания «Shift+:» или панели «Калькулятор».
Арифметические операции сложения, вычитания, умножения и деления вводятся нажатием клавиш «+», «-», «*», «/». Также это можно сделать при помощи панели «Калькулятор».
Функции квадратного корня или корня n-й степени, sin, cos, tg и т.д. также находятся на ней. Следует обратить внимание, что тангенс обозначается как tan, а арктангенс – atan.
Степень числа можно ввести командой «Shift+^», а число π – с панели «Греческий» (см. рис. 1.2.1)
Рис 1.2.1. Рабочие панели инструментов Mathcad 15
Для вычисления какого-либо параметра требуется сначала написать формулу, по которой он определяется в соответствии с приведенными выше рекомендациями. В данном случае вместо знака «=» также используется знак присваивания «:=». А для вывода результата вычисления, необходимо осуществить ввод символа, обозначаемого величину, значение которой нужно вычислить, а затем нажать «=» на клавиатуре либо с панели «Калькулятор».
Мнимая единица обозначается как «1i» и автоматически преобразуется в «i».
Формула всегда должна располагаться на странице ниже данных, которые в нее входят, иначе символы выделяются красным цветом и переменная считается не определенной.
В Mathcad можно также добавлять подписи. Для этого следует на пустом поле начать вводить слова, и программа автоматически распознает их как текстовый формат. Для изменения формата текста, требуется щелкнуть по нему левой кнопкой мышки, выделить, а затем правой кнопкой выбрать подменю «Шрифт».
В качестве примера рассмотрим ввод исходных данных из задания: a, b, h, l, f, Em, q, ε0, μ0, ε, μ, σ, tgδ (рис. 1.2.2).
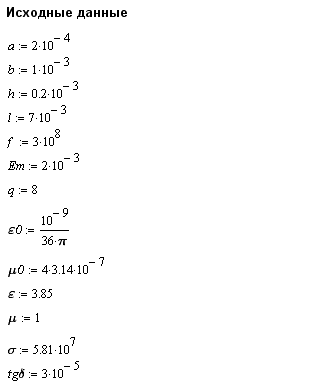
Рис 1.2.2. Пример ввода исходных данных в Mathcad 15
Теперь рассчитаем первичные и вторичные параметры длинной линии по формулам 1.2.1 – 1.2.5. Если параметр является функцией частоты ω, то она обязательно указывается в круглых скобках, например, R0(ω) (рис. 1.2.3).

Рис 1.2.3. Пример расчета первичных и вторичных параметров линии в Mathcad 15
Для построения графиков функций требуется нажать на пиктограмму  из панели «График». Затем на оси ординат вместо средней черной точки написать саму функцию с указанием в скобках параметра, от которого она зависит, а вместо крайних – нижний и верхний предел изменения функции, например, R0(ω) , диапазон: 0÷80. На оси абсцисс, где находится посередине черная точка, пишется аргумент ω, а там, где крайние точки – аналогично, как и на вертикальной оси – пределы его изменения, например, 0÷1011 (рис. 1.2.4).
из панели «График». Затем на оси ординат вместо средней черной точки написать саму функцию с указанием в скобках параметра, от которого она зависит, а вместо крайних – нижний и верхний предел изменения функции, например, R0(ω) , диапазон: 0÷80. На оси абсцисс, где находится посередине черная точка, пишется аргумент ω, а там, где крайние точки – аналогично, как и на вертикальной оси – пределы его изменения, например, 0÷1011 (рис. 1.2.4).

Рис 1.2.4. Ввод параметров на график
Чтобы график построился необходимо щелкнуть левой кнопкой мышки на пустое поле. Нажатие на область построения двойным щелчком приведет к открытию окна свойств под названием «Форматирование выбранного графика X-Y». На вкладке «Оси X,Y» для более точного вывода значений можно поставить галочку «сетка» на оси X и на основной оси Y. При помощи снятия галочки «Автосетка» и ввода значения в графу «количество сеток» меняется ее шаг.
Двойной щелчок мыши по закрашенному зеленому прямоугольнику, расположенному справа от надписи «Линии сетки» откроет окно «Цвет», где выбирается ее цвет. На вкладке «Трассировка», в пункте «Обозначение легенды», «Кривая 1», можно изменить тип линии, ее толщину и цвет. На вкладке «Подписи» можно ввести название заголовка и осей X и Y.
На рис. 1.2.5 – 1.2.10 показан пример построения первичных и вторичных параметров длинной линии, перечисленных ранее.
|
|
Рис 1.2.5. Зависимость погонного сопротивления от частоты

Рис 1.2.6. Зависимость погонной проводимости от частоты
|
|
Рис 1.2.7. Зависимость коэффициента ослабления от частоты
|
|
Рис 1.2.8. Зависимость коэффициента фазы от частоты
|
|
Рис 1.2.9. Зависимость волнового сопротивления от частоты
|
|
Рис 1.2.10. Зависимость фазы волнового сопротивления от частоты
Описание входных сигналов
Импульсный сигнал.
Импульсным сигналом называется сигнал напряжения или тока в цепи, отличный от нуля на конечном промежутке времени.
В качестве примера рассмотрим идеальный прямоугольный импульс напряжения e(t) амплитудой Em. Для его формирования используется единичное ступенчатое воздействие, у которого также есть другое название – функция Хевисайда 1(t).
Она имеет следующее описание:
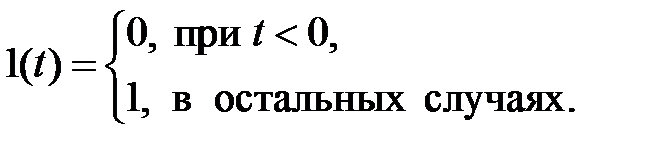 (1.3.1)
(1.3.1)
Существует и другое определение данной функции, отличающееся от предыдущего тем, что при t=0, 1(t) принимает значение, равное 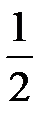 :
:
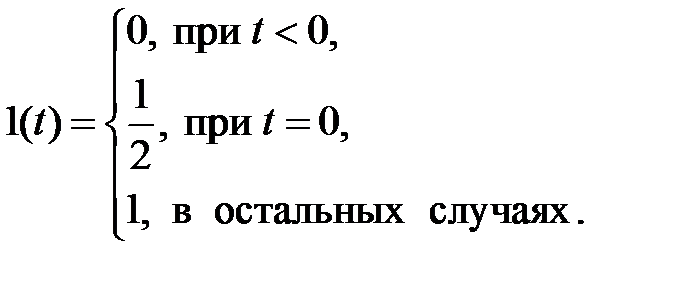 (1.3.2)
(1.3.2)
Сигнал 1(t), приходящий с задержкой на время τ, обозначается как 1(t - τ).
Окончательное описание входного импульсного сигнала e(t) получается из формулы:
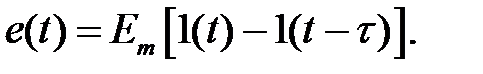 (1.3.3)
(1.3.3)
Для построения импульса, симметричного относительно нуля используется следующее выражение:
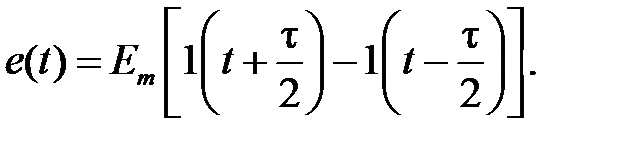 (1.3.4)
(1.3.4)
Способы формирования импульса e(t) согласно формулам (1.3.3) и (1.3.4) показаны на рис. 1.3.1. и рис. 1.3.2 соответственно.
| 1(t) |
| t |
| 0 |
| e(t) |
| t |
| t |
| 0 |
| τ |
| 0 |
| 1(t-τ) |
|
| Em |
Рис 1.3.1. Формирование идеального прямоугольного импульса
|
| t |
| 0 |
| e(t) |
| t |
| t |
| 0 |
| 0 |
| Em |

|
|
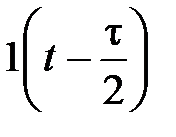
|
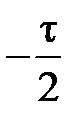
|

|
Рис 1.3.2. Формирование симметричного прямоугольного импульса
Функции можно также описывать, применяя разложение в тригонометрический ряд Фурье:
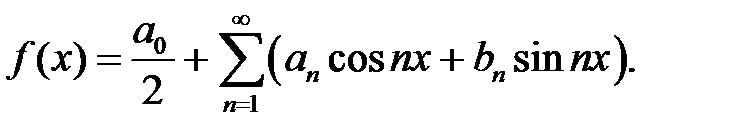 (1.3.5)
(1.3.5)
где коэффициенты ряда a0, an, bn вычисляются по формулам:

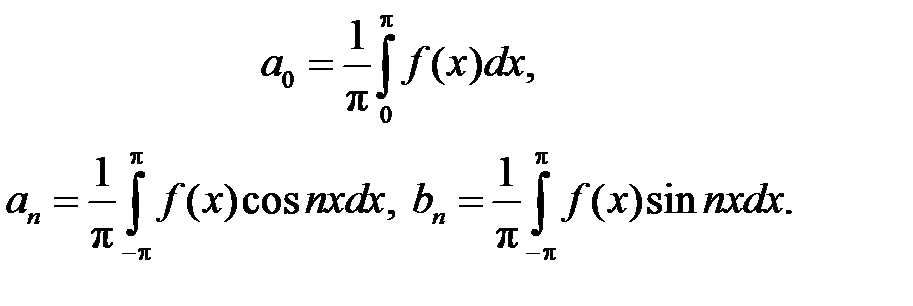 (1.3.6)
(1.3.6)
Заменяя в выражении (1.3.6) f(x) на Em, объединяя синусы и косинусы одной частоты, подставляя в (1.3.5) и заменяя предел суммы конечным пределом, получаем приближенное представление импульсного сигнала рядом Фурье:
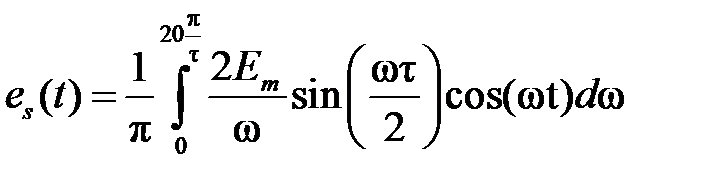 (1.3.7)
(1.3.7)
где τ – длительность импульса, определяемая из выражения:
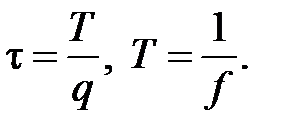 (1.3.8)
(1.3.8)
Переменная q представляет собой скважность и показывает во сколько раз период следования импульсов T превышает их длительность τ. Эти параметры используют для описания периодического сигнала, который будет рассмотрен далее.
Спектральная плотность сигнала представляет собой отношение сигнала на одной частоте на малом интервале времени к его ширине и может быть вычислена по формуле:
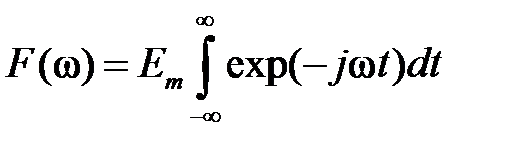 (1.3.9)
(1.3.9)
Это выражение носит название прямого преобразования Фурье.
Применяя обратное преобразование Фурье, можно восстановить импульсный сигнал как функцию времени:
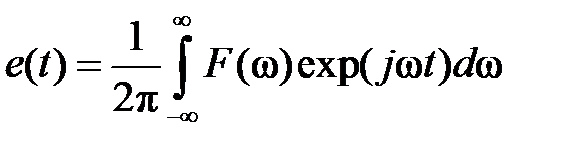 (1.3.10)
(1.3.10)
Пределы интегрирования в (1.3.9) и (1.3.10) обычно заменяют на конечные 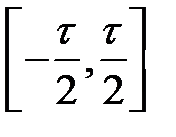 .
.
Периодический сигнал.
В качестве периодического сигнала будет рассматривать последовательность прямоугольных импульсов eT(t), имеющих период следования T, длительность τ и амплитуду Em (рис. 1.3.3).
| б) |
| 0 |
| t |
| 0 |
| Em |
| eT(t) |
| T |
| а) |
| Em |
| T |
| eT(t) |
| τ |
| τ |
| t |
Рис 1.3.3. Периодический сигнал а) нечетная функция, б) четная функция
Его упрощенное описание в виде последовательности двух импульсов имеет вид:
 (1.3.11)
(1.3.11)
Периодический сигнал имеет дискретное спектральное представление:

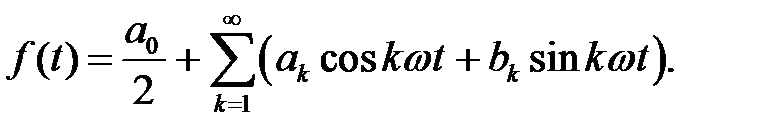 (1.3.12)
(1.3.12)
где k=1,2..∞, ω – частота основной гармоники.
Коэффициенты ряда a0, an, bn вычисляются по формулам:

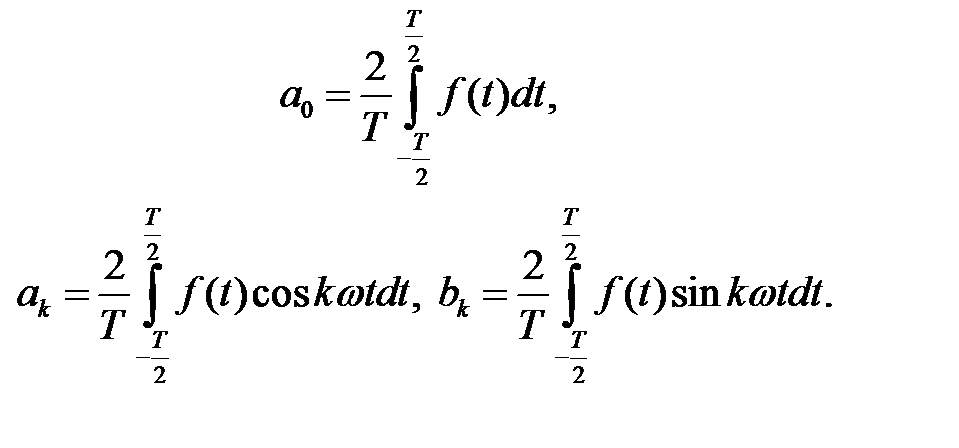 (1.3.13)
(1.3.13)
Если сигнал представляет собой нечетную функцию времени (рис. 1.3.3, а), то в тригонометрической записи ряда Фурье (1.3.12) остаются только синусоидальные составляющие bk. Для четной функции времени (рис. 1.3.3, б) в нуль обращаются коэффициенты bk, и ряд содержит только косинусоидальные составляющие ak.
Так, сигнал eT(t) из рис. 1.3.3, б при bk=0,  и f(t)=Em на интервале
и f(t)=Em на интервале 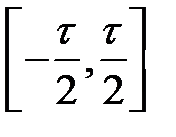 , согласно формулам (1.3.12) и (1.3.13) может быть представлен рядом Фурье:
, согласно формулам (1.3.12) и (1.3.13) может быть представлен рядом Фурье:

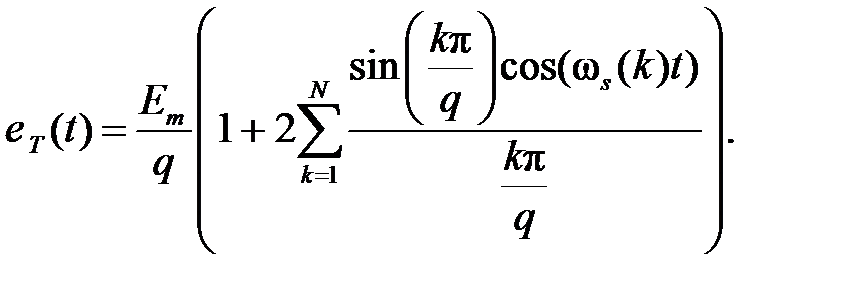 (1.3.14)
(1.3.14)
Здесь круговая частота изменяется дискретно 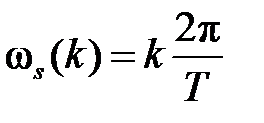 . Число гармоник N определяет точность приближения функции (1.3.14) к идеальной (см. рис. 1.3.3, б).
. Число гармоник N определяет точность приближения функции (1.3.14) к идеальной (см. рис. 1.3.3, б).
Пример составления модели сигналов в ППП Mathcad 15.
Для составления модели импульсного сигнала необходима функция Хевисайда. Алгоритм, описывающий единичный ступенчатый скачок Hev(t) согласно выражению (1.3.2) имеет следующую словесную формулировку: если t<0, то Hev(t)=0, иначе, если t=0, то Hev(t)= 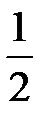 , иначе Hev(t)=1.
, иначе Hev(t)=1.
Для его реализации в Mathcad применяется панель инструментов «Программирование» с условным оператором «if», имеющий синтаксис if(условие 1, значение 1, if (условие 2, значение 2, значение3)). При этом условие 1 соответствует t<0, значение 1 – Hev(t)=0, условие 2 – t=0, значение 2 – Hev(t)= 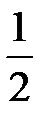 , значение 3 – Hev(t)=1.
, значение 3 – Hev(t)=1.
Прямоугольный импульс можно описать, используя обратное преобразование Фурье от его спектральной плотности (1.3.10).
В программе существует готовая команда, выполняющая его, на панели «Символьные» под названием «invfourier». При этом сначала пишется буквенное обозначение сигнала, затем знак присваивания, например «ee(t):=», а далее вызывается указанный оператор и слева от него, вместо черной точки вводится функция F(ω). Произойдет автоматическое преобразование, где символом Φ Mathcad обозначает функцию Хэвисайда. Результат отобразится после стрелки, стоящей справа от invfourier.
Для ввода интеграла при вычислении F(ω) и es(t) применяется панель «Математический анализ».
Пример вычисления параметров импульса, а также функций 1(t), e(t), es(t), T, τ, F(ω), по формулам (1.3.2 – 1.3.4, 1.3.7 – 1.3.10) приведен на рис. 1.3.4. При этом несимметричный импульс обозначен как e(t), симметричный – e _(t), полученный при помощи обратного преобразования Фурье – e __(t). Графики различных представлений импульсного сигнала показаны на рис. 1.3.5 – 1.3.8, а спектральная плотность – на рис. 1.3.9. Ее необходимо строить по модулю и в первой четверти.

Рис 1.3.4. Пример вычисления параметров импульсного сигнала
|
|
Рис 1.3.5. Несимметричный импульсный сигнал
|
|
Рис 1.3.6. Симметричный импульсный сигнал
|
|
Рис 1.3.7. Симметричный импульсный сигнал,
полученный при помощи обратного преобразования Фурье
|
|
Рис 1.3.8. Симметричный импульсный сигнал,
представленный разложением в ряд Фурье
|
|

Рис 1.3.9. Спектральная плотность импульсного сигнала
Теперь в качестве примера рассмотрим описание в Mathcad периодического сигнала (рис. 1.3.3, а). Здесь также может быть использован оператор «if», имеющий синтаксис if(условие 1, значение 1, if (условие 2, значение 2, if (условие 3, значение 3, if (условие 4, значение 4, значение 5)))). При этом условие 1 соответствует t<0, значение 1 – eT(t)=0, условие 2 – t<τ, значение 2 – eT(t)=Em, условие 3 – t<T, значение 3 – eT(t)=0, условие 4 – t<T+τ, значение 4 – eT(t)= Em, значение 5 – eT(t)= 0 согласно формуле (1.3.11).
Расчетные формулы для идеального периодического сигнала eT(t), ωs(k) и сигналов eTs 15(t), eTs 30(t), eTs 100(t), представленных разложением в ряд Фурье (1.3.14) для N=15, N=30 и N=100 гармоник соответственно приведены на рис. 1.3.10. При этом оператор суммы можно найти на панели «Математический анализ». Для построения нескольких характеристик на одном графике, необходимо выставить курсор справа от написанного параметра на оси ординат и нажать «,» на английской раскладке клавиатуры. Графики различного представления периодических сигналов показаны на рис. 1.3.11, 1.3.12. Из рис. 1.3.12 видно, что с увеличением N сигнал все сильнее приближается к идеальной последовательности импульсов.

Рис 1.3.10. Расчетные формулы для формирования периодического сигнала
|
|
Рис 1.3.11. Идеальный периодический сигнал
|
|
Рис 1.3.12. Периодический сигнал, представленный разложением в ряд Фурье
Описание выходных сигналов
Дата: 2019-03-05, просмотров: 468.










