Рассматривая линии передачи, их условно можно разделить на три группы: линии с сосредоточенными параметрами, линии с распределенными параметрами и комбинированные линии (рис. 1.1.1).
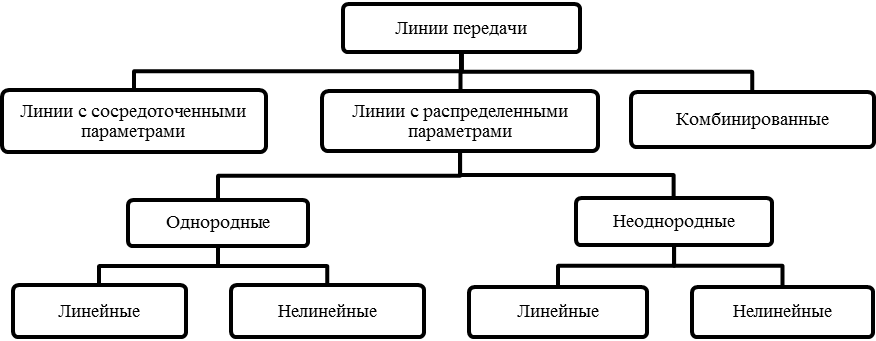
Рис. 1.1.1. Классификация линий передачи
В первом случае электрическое поле сконцентрировано в пределах конденсатора и катушки индуктивности, а потери мощности – в резисторе. При этом вводят допущение, что значение тока в пределах одной ветви на всех элементах цепи одинаково. Однако оно справедливо, если геометрические размеры устройства, намного меньше, чем длина волны распространяющегося в системе электромагнитного колебания l<<λ. Изменения сигнала в любой точке и в конце цепи происходят одновременно с его изменением на ее входе. Он не запаздывает и является только функцией времени.
Во втором случае указанные параметры распределены вдоль всей цепи. Такие устройства имеют продольные размеры, значительно превышающие длину волны или сравнимые с ней, а поперечные – значительно меньше длины волны. Поэтому указанные выше допущения в данном случае уже вводить нельзя. Цепи с распределенными параметрами также называют длинными или полосковыми линиями. Если длина волны равна длине цепи l=λ, то изменение выходного сигнала (напряжения, тока) в конце линии происходит с запаздыванием на Т.
В случае, когда l>λ, запаздывание входного сигнала составляет несколько периодов колебаний. Если же l>>λ, то сигнал цепи является не только функцией времени, но и расстояния от начала цепи (координаты).
Если параметры цепи распределены вдоль линии равномерно, то такая длинная линия называется однородной, в противном случае – это неоднородная линия. Каждая из них в свою очередь может быть линейной, когда передаточная характеристика цепи представляет прямую линию, и нелинейной, когда она представлена иным законом изменения.
В комбинированных линиях одна и та же цепь может вести себя как система с сосредоточенными или распределенными параметрами в зависимости от длины волны сигнала, действующей на данном участке цепи.
Если не учитывать потери в полосковой линии, то теоретически сигнал должен распространяться через нее без искажений, не изменяя своей формы. Несогласованная нагрузка на выходе и на входе линии вызывает повторные отражения. Однако в реальных линиях всегда присутствуют потери, зависящие от частоты, поэтому даже в случае согласованной нагрузки форма выходного сигнала отличается от формы входного [7].
В данной работе будет рассмотрен вариант, когда к выходу линии с потерями подключена согласованная нагрузка, а ко входу линии подсоединен идеальный источник напряжения, сигнал которого имеет заданную форму. Сигнал испытывает искажения, распространяясь по линии, но отражения от нагрузки нет. В результате на нагрузке выделяется сигнал, искаженный по сравнению с входным сигналом. Целью работы является оценка искажений [7].
На рис. 1.1.2 изображен чертеж длинной линии передачи. Она имеет следующие параметры:
a – толщина, мм;
b – ширина, мм;
h – высота, мм;
L – длина, м.
| заземленная шина |
| a |
| b |
| L |
| h |
| диэлектрик |
| полосковый проводник |
Рис. 1.1.2. Длинная линия передачи
Передача осуществляется в основном вдоль линии в слое диэлектрика и направляется полосковым проводником. Диэлектрик немагнитен, но в нем существуют омические потери. Проводимость полоскового проводника отлична от нуля, а погонное сопротивление может быть высоким, так как высокочастотный сигнал при распространении проникает только в очень узкий слой проводника. Полосковые линии используют в технике сверхвысоких частот (наносекундных импульсов), при этом электромагнитная энергия передается по диэлектрику [7].
Длинную линию можно рассматривать как цепь с бесконечно большим числом звеньев элементарной длины dl с входным u, i и выходными напряжением и током u + du, i + di соответственно, электрические параметры которых бесконечно малы. Отрезок такой линии и его эквивалентная схема замещения изображены на рис. 1.1.3.
а)

б)
Рис. 1.1.3. Отрезок линии длиной dl (а) и его эквивалентная схема (б).
Элементарный участок длиной dl длинной линии представляет собой четырехполюсник.
Погонные параметры схемы замещения, такие как индуктивность Ldl, емкость Cdl, сопротивление Rdl, проводимость Gdl будут подробно рассмотрены в пункте 1.2.
Дата: 2019-03-05, просмотров: 378.