Цель занятия: получить практические навыки обработки результатов измерений по обнаружению грубых погрешностей с использованием критерия Романовского.

Задание. Решить задачи, номера которых приведены в табл. 3.2, согласно полученному варианту.

Методические указания

Грубой погрешностью (промахом) называется погрешность, существенно превышающая значение ожидаемой погрешности при данных условиях проведения измерительного эксперимента. Обычно грубая погрешность является следствием значительного внезапного изменения условий эксперимента: скачка тока источника электропитания; не учтённое экспериментатором изменение температуры окружающей среды (при длительном эксперименте); неправильный отсчёт показаний из-за отвлечения внимания экспериментатора и др. Наличие грубых погрешностей в выборке результатов измерений могут сильно исказить среднее значение выборки и как следствие доверительный интервал. Поэтому выявление и исключение результатов, содержащих промах, обязательно.

Обычно результат измерения, содержащий грубую погрешность, сразу виден в ряду измеренных значений, но в каждом конкретном случае это необходимо доказать. Одним из критериев для оценки промаха является критерий Романовского.

В этом случае используют уровень значимости β, который определяется равенством

где Мх  – среднее арифметическое

где n – количество измерений.

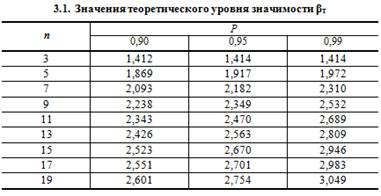
В зависимости от выбранной доверительной вероятности Р, т.е. от желания экспериментатора получить уверенный результат проверки гипотезы, и числа измерений n из табл. 2.1 находят теоретический уровень значимости βт и сравнивают с ним рассчитанное значение β. Если β > βт, то результат х_min/max следует отбросить как содержащий грубую погрешность. Если β < βт, то выборку следует сохранить в полном объёме.

Как правило, критерий Романовского применяют при объёме выборки n < 20.

         Пример решения задачи

       При многократном измерении напряжения электрического тока с помощью цифрового вольтметра получены значения в В: 10,38; 10,37; 10,39; 10,38; 10,39; 10,44; 10,41; 10,5; 10,45; 10,39; 11,1; 10,45. Проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р = 0,95.

Решение.

        1. По формуле (3.2) находится среднее арифметическое значение Мх

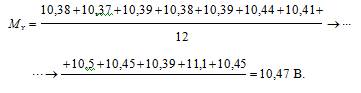
        2. По формуле (3.3) рассчитывается среднее квадратическое отклонение Sx данного ряда

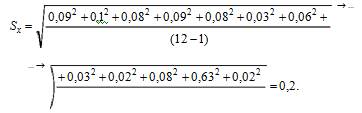
        3.Из ряда измеренных значений напряжения выбираем результаты, подозрительные на содержание грубой погрешности: наименьший х_min = 10,37 В и наибольший х_max = 11,1 В.

        Рассчитываем критерий β_min для х_min = 10,37 В по формуле (3.1)

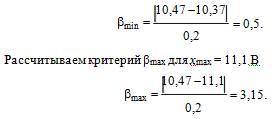
       4.Из таблицы 3.1 при заданном значении доверительной вероятности Р = 0,95 и числа измерений n = 12 находим теоретический уровень значимости βт для данного ряда

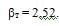
Примечание. Значение βт для n = 12 находится следующим образом

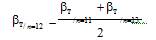
Аналогично находятся значения βт для всех чётных значений n.

        5.Сравниваем значения βmin и βmax с найденным значением βт:

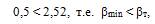
следовательно результат хmin = 10,37 В не содержит грубую погрешность и его следует оставить в ряду измеренных значений.

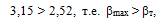
        6.После исключения промаха из ряда значений необходимо пере- считать значения Мх, Sx, βmin и βmax, так как изменилось х_max (х_max = 10,5 В) и количество измерений n (n = 11).

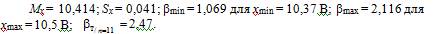
       Как видно 1,069 < 2,47, т.е. βmin < βт, и 2,11 < 2,47, т.е. βmax < βт. Из приведённых расчётов следует, что полученный ряд измеренных значений напряжения электрического тока не содержит промахов с вероятностью Р = 0,95.

Задачи для самостоятельного решения

       При многократном измерении физической величины Х получен ряд измеренных значений. Используя критерий Романовского, необходимо проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р.

Таблица 2.2. Исходные данные