САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Гагарина Ю.А.
Методические указания
к практическим занятиям по курсу «Основы метрологии, стандартизации, сертификации и контроля качества»
для студентов направления 08.03.01 «Строительство» (СТЗС) профилей:
Профиль 1. Производство строительных материалов, изделий и конструкций.
Профиль 2. Промышленное и гражданское строительство.
Профиль 3. Автомобильные дороги и аэродромы.
Профиль 4. Теплогазоснабжение и вентиляция.
Профиль 5. Мосты и транспортные тоннели.
Профиль 6. Водоснабжение и водоотведение.
Профиль 7. Экспертиза и управление недвижимостью.
Утверждена на заседании УМК
по направлению 08.03.01 (08.04.01) «Строительство»
Протокол №12 от 29.05.2015г.
Председатель УМКН Иващенко Ю.Г.
Саратов – 2015
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составители: Тимохин Денис Константинович, Кочергина Мария Петровна
Под редакцией Д.К.Тимохина
Рецензент А.В. Страхов
410054, Саратов, ул. Политехническая, 77
ИОС СГТУ http://www.sstu.ru/obrazovanie/ios/
© Саратовский государственный
технический университет, 2015
Практическое занятие № 1
ВЫЧИСЛЕНИЕ АБСОЛЮТНЫХ, ОТНОСИТЕЛЬНЫХ И ПРИВЕДЁННЫХ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Цель занятия: получить практические навыки решения задач на вычисление абсолютных, относительных, приведённых погрешностей и вариации показаний приборов.
Задание. Решить задачи, номера которых приведены в п.1.2. согласно полученному варианту.
Пример решения задачи
Задача 1.1. Вольтметром со шкалой (0…100) В, имеющим абсолютную погрешность ΔV = 1 В, измерены значения напряжения 0; 10; 20; 40;
50; 60; 80; 100 В. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение.
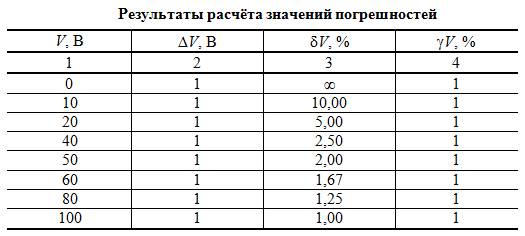
Для записи результатов формируем таблицу (табл. 1.1), в столбцы которой будем записывать измеренные значения V, абсолютные ΔV, относительные δV и приведённые γV погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 В.
Значение абсолютной погрешности известно из условий задачи (ΔV = 1 В) и считается одинаковым для всех измеренных значений напряжения; это значение заносим во все ячейки второго столбца.
Значения относительной погрешности будем рассчитывать по формуле:
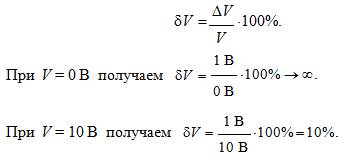
Значения относительной погрешности для остальных измеренных значений напряжения рассчитываются аналогично.
Полученные таким образом значения относительной погрешности заносим в третий столбец.
Для расчёта значений приведённой погрешности будем использовать формулу:
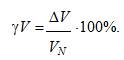
Предварительно определим нормирующее значение VN .Так как диапазон измерений вольтметра – (0…100) В, то шкала вольтметра содержит нулевую отметку, следовательно, за нормирующее значение принимаем размах шкалы прибора, т.е.
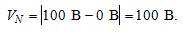
Так как величины ΔV и VN постоянны при любых измеренных значениях напряжения, то величина приведённой погрешности так же постоянна и составляет:
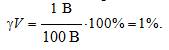
Эти значения заносим во все ячейки четвертого столбца.
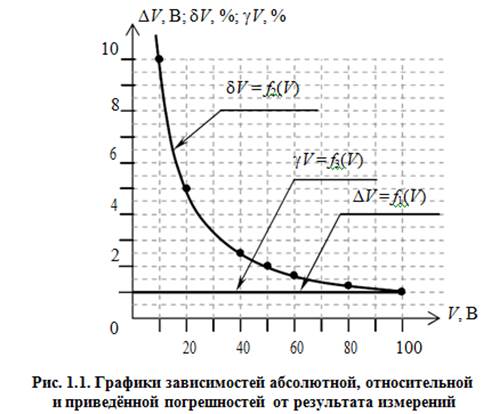
По данным табл. 1.1 строим графики зависимостей абсолютной ΔV, относительной δV и приведённой γV погрешностей от результата измерений V (рис. 1.1).
В данном случае графики зависимостей абсолютной и приведённой погрешностей сливаются друг с другом и представляют собой горизонтальные прямые линии. График зависимости относительной погрешности представляет собой гиперболу.
Внимание: так как диапазон измерений прибора – (0…100) В, то за пределы этого диапазона построенные графики не должны выходить.
Таблица 1.1.
1.2. Задачи для самостоятельного решения
Задача 1. Омметром со шкалой (0...1000) Ом измерены значения 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Определить значения абсолютной и относительной погрешностей, если приведённая погрешность равна 0,5. Результаты представить в виде таблицы и графиков.
Задача 2. Амперметром со шкалой (0…50) А, имеющим относительную погрешность δI = 2%, измерены значения силы тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Задача 3. Вольтметром со шкалой (0…50) В, имеющим приведенную погрешность γV = 2%, измерены значения напряжения 0; 5; 10; 20; 40; 50 В. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Задача 4. Кислородомером со шкалой (0...25) % измерены следующие значения концентрации кислорода: 0; 5; 10; 12,5; 15; 20; 25%. Определить значения абсолютной и относительной погрешностей, если приведённая погрешность равна 2%. Результаты представить в виде таблицы и графиков.
Задача 5. Расходомером со шкалой (0…150) м3/ч, имеющим относительную погрешность δQ = 2%, измерены значения расхода 0; 15; 30; 45;60; 75; 90; 105; 120; 135; 150 м3/ч. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ РАЗЛИЧНЫХ СПОСОБАХ ЗАДАНИЯ КЛАССОВ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
Цель занятия: получить практические навыки решения задач на вычисление погрешностей при различных способах задания классов точности приборов.
Задание. Решить задачи, номера которых приведены в табл. 2.2, согласно полученному варианту.
Пример решения задачи
Задача 2.1. Амперметром класса точности 2.0 со шкалой (0…50) А измерены значения тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимо- сти абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение.
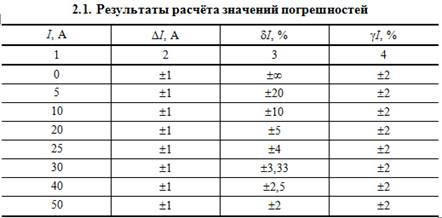
Для записи результатов формируем таблицу (табл. 2.1), в столбцы которой будем записывать измеренные значения I, абсолютные ΔI, относительные δI и приведённые γI погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения тока: 0; 5; 10; 20; 25; 30; 40; 50 А.
Класс точности амперметра задан числом без кружка, следовательно, приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |γI | ≤ 2%.
При решении задачи рассмотрим худший случай |γI| = 2%, когда приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует γI = +2% и γI = –2%.
Данные значения приведённой погрешности заносим в четвёртый столбец табл. 2.1.
Рассчитаем значения абсолютной погрешности.
Из формулы:
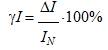
выражаем абсолютную погрешность:
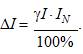
За нормирующее значение IN принимаем размах шкалы, т.к шкала амперметра содержит нулевую отметку
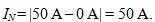
Абсолютная погрешность равна:
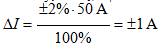
во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.
Значения относительной погрешности будем рассчитывать по формуле:
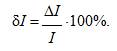
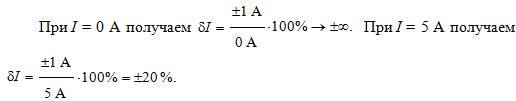
Значения относительной погрешности для остальных измеренных значений тока рассчитываются аналогично.
Полученные таким образом значения относительной погрешности заносим в третий столбец.
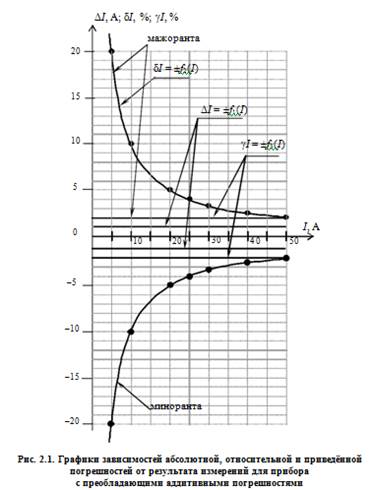
По данным табл. 2.1, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной ΔI, относительной δI и приведённой γI погрешностей от результата измерений I (рис. 2.1).
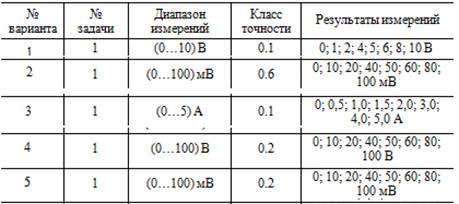
Задачи для самостоятельного решения
Для прибора рассчитать значения абсолютных, относительных и приведённых основных погрешностей измерений. Результаты представить в виде таблицы и графиков.
Таблица 2.2.
Практическое занятие № 2
Методические указания
Грубой погрешностью (промахом) называется погрешность, существенно превышающая значение ожидаемой погрешности при данных условиях проведения измерительного эксперимента. Обычно грубая погрешность является следствием значительного внезапного изменения условий эксперимента: скачка тока источника электропитания; не учтённое экспериментатором изменение температуры окружающей среды (при длительном эксперименте); неправильный отсчёт показаний из-за отвлечения внимания экспериментатора и др. Наличие грубых погрешностей в выборке результатов измерений могут сильно исказить среднее значение выборки и как следствие доверительный интервал. Поэтому выявление и исключение результатов, содержащих промах, обязательно.
Обычно результат измерения, содержащий грубую погрешность, сразу виден в ряду измеренных значений, но в каждом конкретном случае это необходимо доказать. Одним из критериев для оценки промаха является критерий Романовского.
В этом случае используют уровень значимости β, который определяется равенством
где Мх – среднее арифметическое
где n – количество измерений.
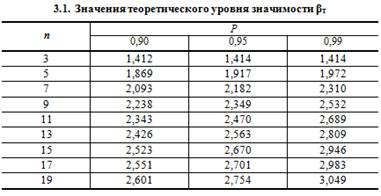
В зависимости от выбранной доверительной вероятности Р, т.е. от желания экспериментатора получить уверенный результат проверки гипотезы, и числа измерений n из табл. 2.1 находят теоретический уровень значимости βт и сравнивают с ним рассчитанное значение β. Если β > βт, то результат хmin/max следует отбросить как содержащий грубую погрешность. Если β < βт, то выборку следует сохранить в полном объёме.
Как правило, критерий Романовского применяют при объёме выборки n < 20.
Пример решения задачи
При многократном измерении напряжения электрического тока с помощью цифрового вольтметра получены значения в В: 10,38; 10,37; 10,39; 10,38; 10,39; 10,44; 10,41; 10,5; 10,45; 10,39; 11,1; 10,45. Проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р = 0,95.
Решение.
1. По формуле (3.2) находится среднее арифметическое значение Мх
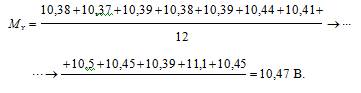
2. По формуле (3.3) рассчитывается среднее квадратическое отклонение Sx данного ряда
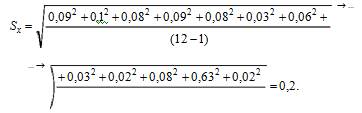
3.Из ряда измеренных значений напряжения выбираем результаты, подозрительные на содержание грубой погрешности: наименьший хmin = 10,37 В и наибольший хmax = 11,1 В.
Рассчитываем критерий βmin для хmin = 10,37 В по формуле (3.1)
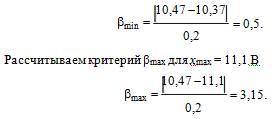
4.Из таблицы 3.1 при заданном значении доверительной вероятности Р = 0,95 и числа измерений n = 12 находим теоретический уровень значимости βт для данного ряда
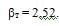
Примечание. Значение βт для n = 12 находится следующим образом
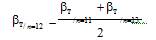
Аналогично находятся значения βт для всех чётных значений n.
5.Сравниваем значения βmin и βmax с найденным значением βт:
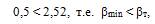
следовательно результат хmin = 10,37 В не содержит грубую погрешность и его следует оставить в ряду измеренных значений.
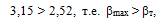
6.После исключения промаха из ряда значений необходимо пере- считать значения Мх, Sx, βmin и βmax, так как изменилось хmax (хmax = 10,5 В) и количество измерений n (n = 11).
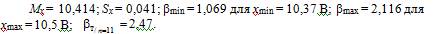
Как видно 1,069 < 2,47, т.е. βmin < βт, и 2,11 < 2,47, т.е. βmax < βт. Из приведённых расчётов следует, что полученный ряд измеренных значений напряжения электрического тока не содержит промахов с вероятностью Р = 0,95.
Задачи для самостоятельного решения
При многократном измерении физической величины Х получен ряд измеренных значений. Используя критерий Романовского, необходимо проверить полученные результаты измерений на наличие грубой погрешности с вероятностью Р.
Таблица 2.2. Исходные данные
Методические указания
Результаты многократных наблюдений, получаемые при прямых измерениях величины Х, называются равноточными (равнорассеянными), если они являются независимыми, одинаково распределёнными случайными величинами. Измерения проводятся одним наблюдателем в одинаковых условиях внешней среды и с помощью одного и того же средства измерения.
Доверительными границами погрешности результата измерений называется наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений .
Статистическая обработка группы результатов наблюдения при равноточных измерениях, нормальном распределении, выполняется в такой последовательности .
Задачи для самостоятельного решения
Задача 1. При многократном измерении силы F получены значения в Н: 403; 408; 410; 405; 406; 398; 496; 404. Укажите доверительные границы истинного значения силы с вероятностью Р = 0,95
Задача 2. При многократном измерении силы электрического тока получены значения в А: 0,8; 0,85; 0,8; 0,79; 0,82; 0,78; 0,79; 0,8; 0,84. Укажите доверительные границы истинного значения силы тока с вероятнстью Р = 0,99.
Задача 3. При многократном измерении длины балки L получены значения в мм: 90,3; 90; 89,8; 89,9; 90,4; 90; 90,3; 89,1; 90,5; 90,4; 90. Укажите доверительные границы истинного значения длины с вероятностью Р = 0,95.
Задача 4. При многократном измерении температуры объекта получены значения в °С: 40,4; 41,0; 40,2; 40,0; 43,5; 42,7; 40,3; 40,4; 40,8 °С. Укажите доверительные границы истинного значения температуры с вероятностью Р = 0,99.
Задача 5. При многократном измерении напряжения электрического тока получены значения в В: 263; 268; 273; 265; 267; 261; 266; 264; 267 В. Укажите доверительные границы истинного значения напряжения с вероятностью Р = 0,95.
Практическое занятие № 3
Методические указания
Косвенное измерение это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
Пример решения задачи
Практическое занятие № 4
Методические указания
Группа студентов (2-4 человека) выбирают вопрос занятия и, используя литературные источники, готовят презентацию, материал которой докладывает на занятии.
Задание 2.
Изучите ГОСТ Р 40003 – 2000, «Порядок проведения сертификации систем качества и сертификации производств», ГОСТ 40.005-96 «Инспекционный контроль за сертифицированными системами качества в производствами».
Методические указания
При изучении данного нормативного документа следует письменно ответить на следующие вопросы:
· какова область применения данного стандарта;
· какие цели преследует сертификация систем качества, и какие условия следует соблюдать при этом;
· что является объектом проверки при сертификации систем качества и при сертификации производств;
· кто является субъектом сертификации;
· какие этапы включает сертификация систем качества;
· в каких случаях и на основании каких документов проводится инспекционный контроль;
· кто уполномочен осуществлять инспекционный контроль;
· какие последствия могут возникнуть, если результаты инспекционного контроля будут неудовлетворительными.
Далее следует отметить, какие процедуры сертификации систем качества (производств) осуществляет заявитель.
Практическое занятие № 5
Самостоятельная работа
Вариант 1.
Оцените затраты предприятия на качество и проанализируйте ее структуру, имея следующие данные:
o затраты на метрологическое обеспечение производства (ПЗК) – 24 д.е.
o затраты на испытания и сертификацию (ОЗК) – 5 д.е.;
o затраты, связанные с дефектами на производстве (ДЗК), – 4,7 д.е.;
o затраты, связанные с возвратом недоброкачественной продукции (ЗКВш) – 23 д.е.
Вариант 2.
Оцените затраты предприятия на качество и проанализируйте ее структуру, имея следующие данные:
· затраты на метрологическое обеспечение производства (ПЗК) – 672 тыс. руб.
· затраты на испытания и сертификацию (ОЗК) – 291 тыс. руб.
· затраты, связанные с дефектами на производстве (ДЗК), – 345 тыс. руб.
· затраты, связанные с возвратом недоброкачественной продукции (ЗКВш), – 0 тыс.руб.
Задание 2 . Определение экономического эффекта деятельности предприятия. Установите экономический эффект (Э) от работы предприятия, если известны следующие данные:
· результат экономической деятельности (Р)– 1 700 д.е.;
· затраты на производство (Зп) – 100 д.е.;
· затраты на эксплуатацию (Зэ) – 1 200 д.е.;
· цена изделия (Ц) – 300 д.е.
Методические указания
Экономический эффект рассчитывается по формуле (3):
Э = Р - (Зп +ЗЭ) ±Ц = (Ц - Зп)+[Р - (Ц + Зэ)] = Эп + Ээ, (3)
где Эп – эффект производства;
Ээ -эффект эксплуатации.
Практическое занятие № 6
КАЧЕСТВА ПРЕДПРИЯТИЯ
Цель занятия: углубление представлений о системах менеджмента качества, документальной базе систем качества, отработка навыков в описании процессов, приобретение умений в разработке документов систем качества
Задание. Изучение модели СМК.
Методические указания
Организация, для того чтобы результативно функционировать, должна определить, как управлять многочисленными взаимосвязанными и взаимодействующими процессами. Систематическая идентификация и управление применяемых процессов и особенно взаимодействия таких процессов считаются «процессным переходом». Модель системы менеджмента качества, описанная в семействе стандартов ИСО 9000, основана на процессном подходе. Модель системы, приведенная на рисунке 1, охватывает все требования стандарта ИСО 9001 (разделы 5-8), но не показывает процессы на детальном уровне.
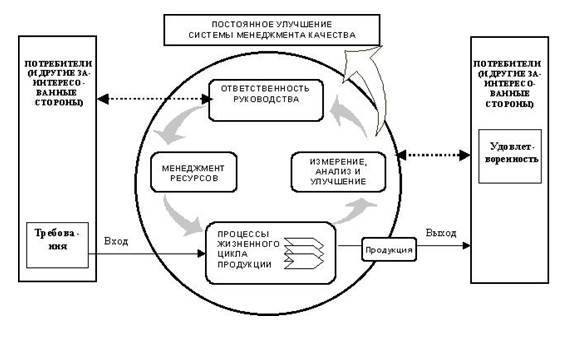
Рисунок 1 – Модель системы менеджмента качества, основанной
на процессном подходе
Условные обозначения:
Деятельность, добавляющая ценность (стоимость)
Информационный поток
Модель системы иллюстративно показывает, что потребитель (заказчик) играет значительную роль в определении входных данных.
Типичные процессы СМК представлены на рисунке 2.
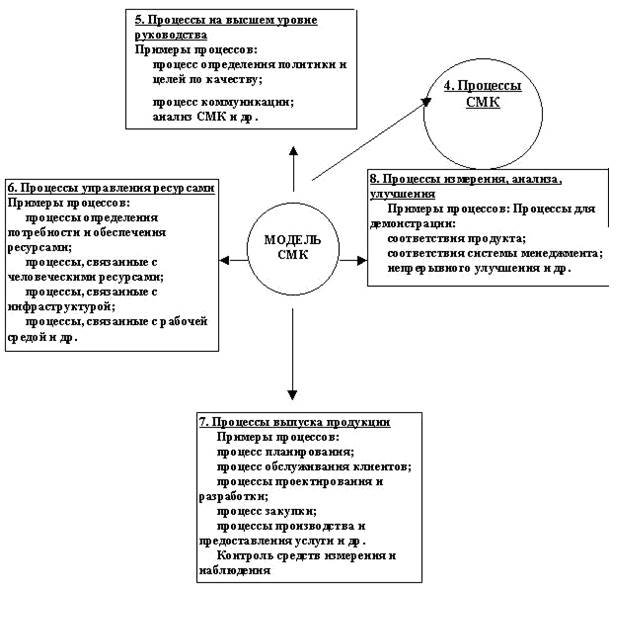
Рисунок 2 – Схематическое представление типичных процессов СМК
Практическое занятие № 7
КАЧЕСТВА ПРЕДПРИЯТИЯ
Цель занятия: углубление представлений о системах менеджмента качества, документальной базе систем качества, отработка навыков в описании процессов, приобретение умений в разработке документов систем качества
Задание. Изучение процедуры декомпозиции процессов.
Методические указания
После того как процессы СМК определены, они поочередно анализируются. Для этого какой-либо процесс, представленный на рисунке 2 (см. практическое занятие №6), сначала рассматривают на макроуровне, чтобы было удобно проследить его взаимосвязь с другими процессами системы или заинтересованными сторонами, а затем осуществляют его структурирование (декомпозицию) до уровня, определяемого поставленной задачей, имеющимися в процессе проблемами, неясностями и т.п. Например, определяя участие подразделений в каком-либо процессе, следует детализировать весь процесс до уровня, на котором проявится их взаимодействие – это будет первый уровень декомпозиции. Если же в какой-то части процесса возникла проблема, то эту часть необходимо детализировать до уровня, на котором будет видна причина проблемы, вплоть до отдельных операций конкретного исполнителя.
Условное изображение декомпозиции процессов по уровням анализа приведено на рисунке 1.
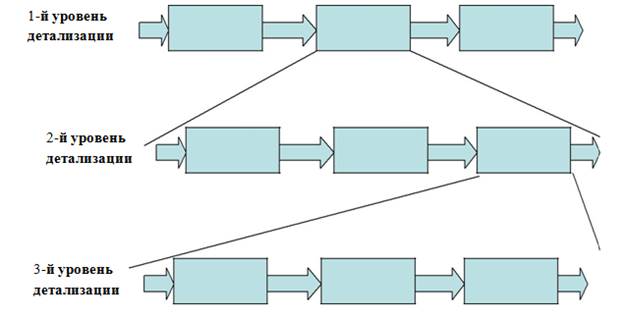
Рисунок 1 – Структурирование (декомпозиция) процессов
Практическое занятие № 8
Пример решения задачи
В таблице приведены ранги, полученные при формализации априорных сведений об одном из процессов. Эксперты, участвовавшие в ранжировании – сотрудники одного предприятия.
В таблице приведены данные по ранжированию параметров одного из процессов. Рассчитать результат ранжирования и оценить согласованность мнений экспертов.
|
Эксперты | Факторы | ||||||
| A | B | C | D | E | F | G | |
| Первый | 1 | 2 | 6 | 4 | 7 | 3 | 5 |
| Второй | 1 | 2 | 7 | 6 | 3 | 5 | 4 |
| Третий | 7 | 1 | 6 | 4 | 2 | 5 | 3 |
| Четвёртый | 3 | 1 | 5 | 6 | 4 | 7 | 2 |
| Пятый | 1 | 2 | 6 | 4 | 5 | 7 | 3 |
1. Рассчитать результат ранжирования и оценить степень согласованности мнений экспертов.
2. Оцените согласованность мнений первого и третьего экспертов.
Решение
Результат расчёта сведём в таблицу:
| Эксперты | Факторы | |||||||
| A | B | C | D | E | F | G | ||
| Суммы Σ а ij | 13 | 8 | 30 | 24 | 21 | 27 | 17 | Среднее L = Σ а ij / 7 = 20 |
| Разности Δ i = Σ а ij - L | -7 | -12 | 10 | 4 | 1 | 7 | -3 | |
| Δ2i | 49 | 144 | 100 | 16 | 1 | 49 | 9 | |
|
S = Σ Δ2ί = 368; m 2 = 25; n 3 – n = 336
| ||||||||
1. Результаты коллективного ранжирования представим в виде ряда, в котором факторы расположены в порядке возрастания суммы их рангов:
Суммы рангов 8 13 17 21 24 27 30
Факторы B A G E D F C
Коэффициент конкордации W = 0,526 является значимым для уровня значимости α = 0,01 . Можно считать, что имеет место неслучайная согласованность во мнениях всех пяти экспертов.
2. Для сравнения мнений 1-го и 3-го экспертов составим таблицу:
Факторы A B C D E F G
Ранги 1-го эксперта 1 2 6 4 7 3 5
Ранги 3-го эксперта 7 1 6 4 2 5 3
d -6 1 0 0 5 -2 2
d 2 36 1 0 0 25 4 4 Σ = 70
Согласованность мнений экспертов оценим с помощью коэффициента ранговой корреляции:
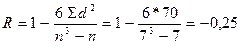
Таким образом, мнения экспертов противоположны (знак минус) и практически не согласуются.
Задачи для самостоятельного решения
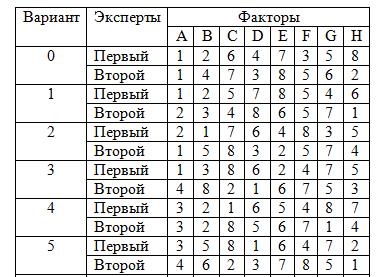
В таблице приведены данные по ранжированию параметров одного из процессов. Рассчитать результат ранжирования и оценить согласованность мнений экспертов.
Практическое занятие № 9
Пример решения задачи
В таблице представлена выписка из рабочего журнала одного из параметров линии по производству листового стекла – съёма стекла (т.е. отношения веса товарной продукции к весу сваренной стекломассы) .
| Число месяца | Тип смены | № бригады | Съём, % | Число месяца | Тип смены | № бригады | Съём, % |
| 1 | Д | 3 | 77 | 16 | Д | 4 | 76 |
| Н | 4 | 76 | Н | 1 | 74 | ||
| 2 | Д | 3 | 73 | 17 | Д | 3 | 75 |
| Н | 4 | 74 | Н | 4 | 68 | ||
| 3 | Д | 2 | 78 | 18 | Д | 3 | 19 |
| Н | 3 | 75 | Н | 4 | 22 | ||
| 4 | Д | 2 | 72 | 19 | Д | 2 | 57,8 |
| Н | 3 | 76 | Н | 3 | 76 | ||
| 5 | Д | 1 | 72 | 20 | Д | 2 | 6 |
| Н | 2 | 72,5 | Н | 3 | 37 | ||
| 6 | Д | 1 | 74 | 21 | Д | 1 | 39 |
| Н | 2 | 79 | Н | 2 | 70 | ||
| 7 | Д | 4 | 79 | 22 | Д | 1 | 70 |
| Н | 1 | 75 | Н | 2 | 77,4 | ||
| 8 | Д | 4 | 78 | 23 | Д | 4 | 76 |
| Н | 1 | 75 | Н | 1 | 76 | ||
| 9 | Д | 3 | 70 | 24 | Д | 4 | 72 |
| Н | 4 | 75 | Н | 1 | 70 | ||
| 10 | Д | 3 | 55 | 25 | Д | 3 | 20,5 |
| Н | 4 | 79 | Н | 4 | 41 | ||
| 11 | Д | 2 | 79 | 26 | Д | 3 | 71 |
| Н | 3 | 73 | Н | 4 | 70 | ||
| 12 | Д | 2 | 72 | 27 | Д | 2 | 78 |
| Н | 3 | 73 | Н | 3 | 70 | ||
| 13 | Д | 1 | 72 | 28 | Д | 2 | 77,7 |
| Н | 2 | 74 | Н | 3 | 73 | ||
| 14 | Д | 1 | 75 | 29 | Д | 1 | 77 |
| Н | 2 | 75,4 | Н | 2 | 77,7 | ||
| 15 | Д | 4 | 76 | 30 | Д | 1 | 78 |
| Н | 1 | 71 | Н | 2 | 70,3 |
Произвести расслоение общей выборки:
1. На дневную и ночную смены. Сравнить выборки, сделать выводы.
2. На смены. Сравнить выборки 1-ой и 2-ой , 1-ой и 3-ей бригад.
3. На смены. Сравнить выборки 1-ой и 4-ой , 2-ой и 3-ей бригад.
4. На смены. Сравнить выборки 2-ой и 4-ой , 3-ей и 4-ой бригад.
Решение
1. Выделим данные в выборки дневной и ночной смен:
| Дневная | Ночная | ||||||||||
| 77 | 74 | 79 | 76 | 39 | 71 | 76 | 79 | 73 | 74 | 70 | 70 |
| 73 | 79 | 72 | 75 | 70 | 78 | 74 | 75 | 73 | 68 | 77,4 | 70 |
| 78 | 78 | 72 | 19 | 76 | 77,7 | 75 | 75 | 74 | 22 | 76 | 73 |
| 72 | 70 | 75 | 57,8 | 72 | 77 | 76 | 75 | 75,4 | 76 | 70 | 77,7 |
| 72 | 55 | 76 | 6 | 20,5 | 78 | 72,5 | 79 | 71 | 37 | 41 | 70,3 |
Рассчитываем характеристики выборок: n = 30;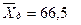 
и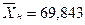 
;
S д = 19,382 и S н = 12,957.
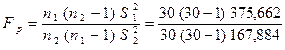= 2,237 . В числитель всегда выносят наибольшую дисперсию. По таблице F-распределения находим при уровне значимости α = 0,05 и степенях свободы k д = 30 – 1 = 29 и k н = 30 – 1 = 29 - F 0,05 = 1,86. Поскольку F p > F табл , дисперсии считаются не равными (S д ≠ S н ).
Для сравнения средних значений выборок принимаем соответствующий t – критерий - приближённый:
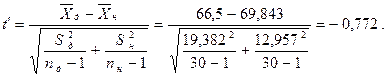
Для расчёта второго компонента критерия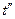 
определяем величину
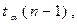которая по таблице для уровня значимости α = 0,05 и n = 30 для дневной и ночной смены будет равна 2,045.
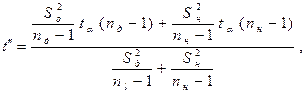
подставив в это выражение численные значения, получим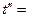 
2,045. Таким образом 
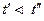, разница между средними дневной и ночной смен несущественна, т.е. условно 
.
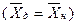2. Выделим из общей выборки данные бригад 1, 2 и 3:
| 1 бр | 72 | 74 | 75 | 75 | 72 | 75 | 71 | 74 | 39 | 70 | 76 | 70 | 77 | 78 | ||
| 2 бр | 78 | 72 | 72,5 | 79 | 79 | 72 | 74 | 75,4 | 57,8 | 6 | 70 | 77,4 | 78 | 77,7 | 77,7 | 70,3 |
| 3 бр | 77 | 73 | 75 | 76 | 70 | 55 | 73 | 73 | 75 | 19 | 76 | 37 | 20,5 | 71 | 70 | 73 |
Характеристики выборок: 1) n 1 = 14;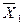 
= 71,286; S 1 = 9,619; 2) n 2 = 16;
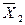= 69,8; S 2 = 17.827; 3) n 3 = 16; 
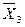= 63,344; S 3 = 19.772 .
Сравним выборки 1 и 2 бригад. Определим:
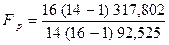= 3.402. По таблице F0,05 = 2,44. Так как Fp > Fтабл , то дисперсии S 1 ≠ S 2. Для сравнения средних воспользуемся приближён-
ным t – критерием. По формулам предыдущего случая соответственно получим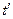 
= 0,279; t α (14 – 1) по таблице = 2,160 и t α (16 – 1) = 2.131 при α = 0,05. Тогда 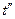= 2,138. Поскольку 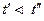, то 
.
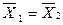Сравним выборки 1 и 3 смен.
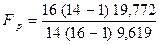= 2.036. По таблице F0.05 = 2,44. Т.к. Fр < Fтабл , то
дисперсии S 1 = S 3. Для сравнения средних воспользуемся точным t – критерием:
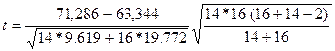= 5,407.
Находим t табл = ± 2,048 и поскольку расчётное значение t – критерия не попадает в критическую область от -2,048 до +2,048, то средние этих выборок существенно различаются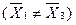 
, имея очевидно для этого какие-то причины.
3. Выделим выборки всех бригад:
| 1 бр | 72 | 74 | 75 | 75 | 72 | 75 | 71 | 74 | 39 | 70 | 76 | 70 | 77 | 78 | ||
| 2 бр | 78 | 72 | 72,5 | 79 | 79 | 72 | 74 | 75,4 | 57,8 | 6 | 70 | 77,4 | 78 | 77,7 | 77,7 | 70,3 |
| 3 бр | 77 | 73 | 75 | 76 | 70 | 55 | 73 | 73 | 75 | 19 | 76 | 37 | 20,5 | 71 | 70 | 73 |
| 4 бр | 76 | 74 | 79 | 78 | 75 | 79 | 76 | 76 | 68 | 22 | 76 | 72 | 41 | 70 |
Характеристики выборок бригад 1, 2 и 3 даны в предыдущем расчёте. Добавим характеристики выборки 4 бригады: n = 14;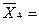 
68,714; S 4 = 16.504.
Сравним выборки 1 и 4 бригад. Определим
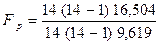= 1,716. Табличное значение F0,05 = 2,57. Поскольку Fp < Fтабл , то S 1 = S 4 . Для сравнения средних используем точный t – критерий:
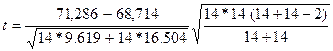= 1,814 .
Табличное значение t 0.05 (14 + 14 - 2) = ± 2,056. Поскольку t p попадает в критическую область от – 2,056 до + 2,056, значит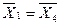 
.
Сравним выборки 2 и 3 бригад. Определим
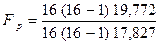= 1,109 . Табличное значение F 0.05 = 2,41. Поскольку Fp < Fтабл , то S 2 = S 3 . Значит используем для сравнения средних точный t – критерий:
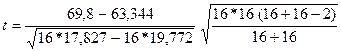= 4,077 .
Табличное значение t 0.05 (16+16-2) = ± 2,042 . Значение t p не попадает в критическую область. Поэтому делаем вывод, что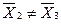 
.
3. Выделим выборки 2, 3 и 4 бригад.
| 2 бр | 78 | 72 | 72,5 | 79 | 79 | 72 | 74 | 75,4 | 57,8 | 6 | 70 | 77,4 | 78 | 77,7 | 77,7 | 70,3 |
| 3 бр | 77 | 73 | 75 | 76 | 70 | 55 | 73 | 73 | 75 | 19 | 76 | 37 | 20,5 | 71 | 70 | 73 |
| 4 бр | 76 | 74 | 79 | 78 | 75 | 79 | 76 | 76 | 68 | 22 | 76 | 72 | 41 | 70 |
Характеристики выборок даны в предыдущих расчётах.
Сравним выборки 2 и 4 бригад:
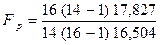= 1,070 . Табличное значение F 0,05 = 2,45 . Поскольку Fp < Fтабл , значит S 2 = S 4 . Для сравнения средних используем точный t – критерий:
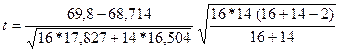= 0,691.
Табличное значение t 0.05 (14+16-2) = 2,048. Поскольку значение t p попадает в критическую область , то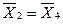 
.
Сравним выборки 3 и 4 бригад:
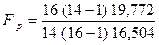= 1,187. Табличное значение F0.05 = 2,45 , значит F p < F табл . Разницы между дисперсиями не обнаружено и, следовательно, для сравнения средних можно применить точный t – критерий:
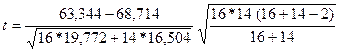= - 3,318 .
Табличное значение t 0.05 (16+14-2) = ± 2,048 . Получается, что значение t p не попадает в критическую область , значит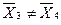 
и тому есть какие-то причины.
Задачи для самостоятельного решения
В таблице представлены данные из рабочего журнала по выходу годной продукции в разные смены за 15 дней разных месяцев.
| Число месяца | Тип смены | № бригады | Выход годной продукции, % | |||||||||
| Варианты задания | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | Д | 3 | 87 | 86 | 86 | 89 | 80 | 87 | 85 | 78 | 85 | 87 |
| Н | 4 | 86 | 84 | 86 | 88 | 82 | 87 | 85 | 79 | 87 | 87 | |
| 2 | Д | 3 | 83 | 85 | 88 | 86 | 80 | 87 | 86 | 79 | 86 | 87 |
| Н | 4 | 84 | 89 | 85 | 86 | 83 | 85 | 84 | 82 | 89 | 89 | |
| 3 | Д | 2 | 88 | 82 | 84 | 86 | 81 | 83 | 87 | 82 | 84 | 82 |
| Н | 3 | 85 | 80 | 83 | 85 | 81 | 82 | 87 | 82 | 85 | 83 | |
| 4 | Д | 2 | 82 | 84 | 82 | 82 | 84 | 80 | 89 | 85 | 85 | 81 |
| Н | 3 | 86 | 86 | 82 | 82 | 86 | 80 | 89 | 84 | 87 | 82 | |
| 5 | Д | 1 | 82 | 86 | 80 | 81 | 83 | 81 | 88 | 86 | 89 | 85 |
| Н | 2 | 82 | 85 | 80 | 80 | 84 | 82 | 85 | 84 | 89 | 83 | |
| 6 | Д | 1 | 84 | 87 | 78 | 80 | 87 | 81 | 85 | 85 | 89 | 82 |
| Н | 2 | 89 | 88 | 76 | 80 | 89 | 81 | 82 | 84 | 86 | 84 | |
| 7 | Д | 4 | 89 | 87 | 77 | 80 | 89 | 83 | 81 | 86 | 87 | 86 |
| Н | 1 | 85 | 89 | 79 | 84 | 90 | 86 | 80 | 87 | 87 | 83 | |
| 8 | Д | 4 | 88 | 88 | 83 | 84 | 89 | 86 | 78 | 85 | 85 | 82 |
| Н | 1 | 85 | 82 | 86 | 85 | 89 | 86 | 77 | 89 | 85 | 85 | |
| 9 | Д | 3 | 82 | 81 | 89 | 87 | 85 | 88 | 79 | 89 | 84 | 87 |
| Н | 4 | 80 | 83 | 89 | 88 | 85 | 89 | 79 | 87 | 83 | 87 | |
| 10 | Д | 3 | 85 | 84 | 88 | 89 | 84 | 89 | 82 | 88 | 85 | 89 |
| Н | 4 | 86 | 85 | 85 | 90 | 82 | 87 | 83 | 86 | 86 | 88 | |
| 11 | Д | 2 | 89 | 87 | 87 | 92 | 82 | 88 | 85 | 84 | 84 | 88 |
| Н | 3 | 89 | 88 | 86 | 89 | 81 | 90 | 86 | 83 | 82 | 89 | |
| 12 | Д | 2 | 83 | 89 | 84 | 89 | 80 | 90 | 86 | 82 | 86 | 91 |
| Н | 3 | 82 | 90 | 82 | 87 | 83 | 90 | 86 | 82 | 83 | 88 | |
| 13 | Д | 1 | 83 | 84 | 83 | 89 | 83 | 88 | 87 | 82 | 85 | 87 |
| Н | 2 | 82 | 82 | 81 | 86 | 85 | 87 | 88 | 82 | 84 | 88 | |
| 14 | Д | 1 | 84 | 80 | 80 | 85 | 86 | 85 | 88 | 85 | 89 | 85 |
| Н | 2 | 85 | 80 | 82 | 84 | 87 | 85 | 88 | 86 | 89 | 85 | |
| 15 | Д | 4 | 86 | 78 | 83 | 86 | 88 | 84 | 89 | 87 | 92 | 86 |
| Н | 1 | 81 | 80 | 83 | 86 | 90 | 82 | 86 | 88 | 91 | 89 | |
Провести расслоение общей выборки:
варианту 1 – на дневную и ночную смены;
варианту 2 – на бригады 1 и 3;
варианту 3 – на бригады 1 и 2
Сравнить выборки и сделать выводы
СПИСОК ЛИТЕРАТУРЫ
1. Аристов О.В. Управление качеством : учебник / О. В. Аристов. – М. : ИНФРА-М, 2007. – 240 с.
2. Басовский Л.Е. Управление качеством : учебник для вузов / Л. Е. Басовский, В.Б. Протасьев. – М. : ИНФРА - М., 2005. – 212 с.
3. Варакута С.А. Управление качеством продукции / С. А. Варакута. – М. : ИНФРА - М, 2001. – 207 с.
4. 4.Пономарев, С.В. Метрология, стандартизация, сертификация : учебник для вузов / С.В. Пономарев, Г.В. Шишкина, Г.В. Мозгова. – Тамбов : Изд-во ГОУ ВПО ТГТУ, 2010. – 96 с.
5. РМГ 29–99. Государственная система обеспечения единства измерений. Метрология. Основные термины и определения. – М. : ИПК Издательство стандартов, 2000. – 50 с.
6. ГОСТ Р 50779.22–2005. Статистические методы. Статистическое представление данных. Точечная оценка и доверительный интервал для среднего. – М. : Стандартинформ, 2005. – 11 с.
7. Колчков, В.И. Метрология, стандартизация и сертификация : учебник / В.И. Колчков. – М. : Гуманитар. изд. центр ВЛАДОС, 2010. – 398 с.
8. Сергеев, А.Г. Метрология : учебник / А.Г. Сергеев. – М. : Логос, 2005. – 272 с.
9. Сергеев, А.Г. Метрология, стандартизация, сертификация : учебное пособие / А.Г. Сергеев, М.В. Латышев, В.В. Терегеря. – М. : Логос, 2003. – 536 с.
10. Димов, Ю.В. Метрология, стандартизация и сертификация : учебник для вузов / Ю.В. Димов. – СПб. : Питер, 2010. – 464 с.
11. Николаев М.И. Метрология, стандартизация, сертификация и управление качеством [Электронный ресурс]/ Николаев М.И.— Электрон. текстовые данные.— М.: Интернет-Университет Информационных Технологий (ИНТУИТ), 2010.— 87 c.-
Режим доступа: http :// www . iprbookshop . ru /16706.— ЭБС «IPRbooks»
12. Латышенко К.П. Технические измерения и приборы. Часть I [Электронный ресурс]: учебное пособие/ Латышенко К.П.— Электрон. текстовые данные.— Саратов: Вузовское образование, 2013.— 480 c.- Режим доступа: http :// www . iprbookshop . ru /20403.— ЭБС «IPRbooks»
13. Радкевич Я.М. Метрология, стандартизация и сертификация [Электронный ресурс]: учебное пособие/ Радкевич Я.М., Схиртладзе А.Г., Лактионов Б.И.— Электрон. текстовые данные.— Саратов: Вузовское образование, 2012.— 790 c.-
Режим доступа: http :// www . iprbookshop . ru /34757.— ЭБС «IPRbooks»
14. Логанина В.И. Аудит систем менеджмента качества [Электронный ресурс]: учебное пособие/ Логанина В.И., Карпова О.В.— Электрон. текстовые данные.— Саратов: Вузовское образование, 2014.— 89 c.— Режим доступа: http://www.iprbookshop.ru/19517.— ЭБС «IPRbooks»
15. Гончаров, А. А. Метрология, стандартизация и сертификация : учеб. пособие / А. А. Гончаров, В. Д. Копылов. - 6-е изд., стер. - М. : ИЦ "Академия", 2008. - 240 с. : ил. - (Высшее профессиональное образование). Экземпляры всего: 50
16. Метрология, стандартизация и сертификация : учеб. / под ред. В. В. Алексеева. - 2-е изд., стер. - М. : ИЦ "Академия", 2008. - 384 с. : ил. - (Высшее профессиональное образование).
Экземпляры всего: 20
17. Соколов, Г. К. Контроль качества выполнения строительно-монтажных работ : справ. пособие / Г. К. Соколов, В. В. Филатов, К. Г. Соколов. - М. : ИЦ "Академия", 2008. - 384 с. - (Высшее профессиональное образование). Экземпляры всего: 25
18. Зайдель, А. Н. Ошибки измерений физических величин : учеб. пособие / А. Н. Зайдель. - 3-е изд., стер. - СПб. ; М. ; Краснодар : Лань, 2009. - 112 с. : ил. - (Учебники для вузов. Специальная литература).
Экземпляры всего: 30
19. Радкевич, Я. М. Метрология, стандартизация и сертификация : учеб. / Я. М. Радкевич, А. Г. Схиртладзе, Б. И. Лактионов. - 3-е изд., перераб. и доп. . - М. : Высшая школа, 2007. - 791 с. : ил.
Экземпляры всего: 25
20. Лукманова И.Г. Создание системы менеджмента качества, охраны здоровья, безопасности и экологии в строительной отрасли [Электронный ресурс]: монография/ Лукманова И.Г., Нежникова Е.В., Аксёнова А.А.— Электрон. текстовые данные.— М.: Московский государственный строительный университет, ЭБС АСВ, 2014.— 136 c.-
Режим доступа: http://www.iprbookshop.ru/30358.— ЭБС «IPRbooks»
21. Метрология: науч.-техн. журнал. - М. : ФГУП «СТАНДАРТИНФОРМ», (1990-2015), №1-12. - ISSN 0132-4713
22. Электронная научная библиотека http://elibrary.ru/defaultx.asp
23. Научная техническая библиотека http://www.twirpx.com
24. Библиотека сайта http://www.allbeton.ru
25. Электронная библиотека: http://window.edu.ru/
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Гагарина Ю.А.
Методические указания
к практическим занятиям по курсу «Основы метрологии, стандартизации, сертификации и контроля качества»
для студентов направления 08.03.01 «Строительство» (СТЗС) профилей:
Профиль 1. Производство строительных материалов, изделий и конструкций.
Профиль 2. Промышленное и гражданское строительство.
Профиль 3. Автомобильные дороги и аэродромы.
Профиль 4. Теплогазоснабжение и вентиляция.
Профиль 5. Мосты и транспортные тоннели.
Профиль 6. Водоснабжение и водоотведение.
Профиль 7. Экспертиза и управление недвижимостью.
Утверждена на заседании УМК
по направлению 08.03.01 (08.04.01) «Строительство»
Протокол №12 от 29.05.2015г.
Председатель УМКН Иващенко Ю.Г.
Саратов – 2015
Все права на размножение и распространение в любой форме остаются за разработчиком.
Нелегальное копирование и использование данного продукта запрещено.
Составители: Тимохин Денис Константинович, Кочергина Мария Петровна
Под редакцией Д.К.Тимохина
Рецензент А.В. Страхов
410054, Саратов, ул. Политехническая, 77
ИОС СГТУ http://www.sstu.ru/obrazovanie/ios/
© Саратовский государственный
технический университет, 2015
Практическое занятие № 1
ВЫЧИСЛЕНИЕ АБСОЛЮТНЫХ, ОТНОСИТЕЛЬНЫХ И ПРИВЕДЁННЫХ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Цель занятия: получить практические навыки решения задач на вычисление абсолютных, относительных, приведённых погрешностей и вариации показаний приборов.
Задание. Решить задачи, номера которых приведены в п.1.2. согласно полученному варианту.
Пример решения задачи
Задача 1.1. Вольтметром со шкалой (0…100) В, имеющим абсолютную погрешность ΔV = 1 В, измерены значения напряжения 0; 10; 20; 40;
50; 60; 80; 100 В. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение.
Для записи результатов формируем таблицу (табл. 1.1), в столбцы которой будем записывать измеренные значения V, абсолютные ΔV, относительные δV и приведённые γV погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения напряжения: 0; 10; 20; 40; 50; 60; 80; 100 В.
Значение абсолютной погрешности известно из условий задачи (ΔV = 1 В) и считается одинаковым для всех измеренных значений напряжения; это значение заносим во все ячейки второго столбца.
Значения относительной погрешности будем рассчитывать по формуле:
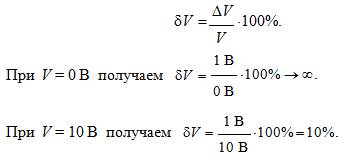
Значения относительной погрешности для остальных измеренных значений напряжения рассчитываются аналогично.
Полученные таким образом значения относительной погрешности заносим в третий столбец.
Для расчёта значений приведённой погрешности будем использовать формулу:
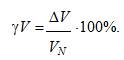
Предварительно определим нормирующее значение VN .Так как диапазон измерений вольтметра – (0…100) В, то шкала вольтметра содержит нулевую отметку, следовательно, за нормирующее значение принимаем размах шкалы прибора, т.е.
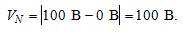
Так как величины ΔV и VN постоянны при любых измеренных значениях напряжения, то величина приведённой погрешности так же постоянна и составляет:
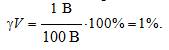
Эти значения заносим во все ячейки четвертого столбца.
По данным табл. 1.1 строим графики зависимостей абсолютной ΔV, относительной δV и приведённой γV погрешностей от результата измерений V (рис. 1.1).
В данном случае графики зависимостей абсолютной и приведённой погрешностей сливаются друг с другом и представляют собой горизонтальные прямые линии. График зависимости относительной погрешности представляет собой гиперболу.
Внимание: так как диапазон измерений прибора – (0…100) В, то за пределы этого диапазона построенные графики не должны выходить.
Таблица 1.1.
1.2. Задачи для самостоятельного решения
Задача 1. Омметром со шкалой (0...1000) Ом измерены значения 0; 100; 200; 400; 500; 600; 800; 1000 Ом. Определить значения абсолютной и относительной погрешностей, если приведённая погрешность равна 0,5. Результаты представить в виде таблицы и графиков.
Задача 2. Амперметром со шкалой (0…50) А, имеющим относительную погрешность δI = 2%, измерены значения силы тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Задача 3. Вольтметром со шкалой (0…50) В, имеющим приведенную погрешность γV = 2%, измерены значения напряжения 0; 5; 10; 20; 40; 50 В. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Задача 4. Кислородомером со шкалой (0...25) % измерены следующие значения концентрации кислорода: 0; 5; 10; 12,5; 15; 20; 25%. Определить значения абсолютной и относительной погрешностей, если приведённая погрешность равна 2%. Результаты представить в виде таблицы и графиков.
Задача 5. Расходомером со шкалой (0…150) м3/ч, имеющим относительную погрешность δQ = 2%, измерены значения расхода 0; 15; 30; 45;60; 75; 90; 105; 120; 135; 150 м3/ч. Рассчитать зависимости абсолютной, относительной и приведённой погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТЕЙ ПРИ РАЗЛИЧНЫХ СПОСОБАХ ЗАДАНИЯ КЛАССОВ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
Цель занятия: получить практические навыки решения задач на вычисление погрешностей при различных способах задания классов точности приборов.
Задание. Решить задачи, номера которых приведены в табл. 2.2, согласно полученному варианту.
Пример решения задачи
Задача 2.1. Амперметром класса точности 2.0 со шкалой (0…50) А измерены значения тока 0; 5; 10; 20; 25; 30; 40; 50 А. Рассчитать зависимо- сти абсолютной, относительной и приведённой основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.
Решение.
Для записи результатов формируем таблицу (табл. 2.1), в столбцы которой будем записывать измеренные значения I, абсолютные ΔI, относительные δI и приведённые γI погрешности.
В первый столбец записываем заданные в условии задачи измеренные значения тока: 0; 5; 10; 20; 25; 30; 40; 50 А.
Класс точности амперметра задан числом без кружка, следовательно, приведённая погрешность, выраженная в процентах, во всех точках шкалы не должна превышать по модулю класса точности, т.е. |γI | ≤ 2%.
При решении задачи рассмотрим худший случай |γI| = 2%, когда приведённая погрешность принимает максимальное по абсолютной величине значение, что соответствует γI = +2% и γI = –2%.
Данные значения приведённой погрешности заносим в четвёртый столбец табл. 2.1.
Рассчитаем значения абсолютной погрешности.
Из формулы:
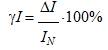
выражаем абсолютную погрешность:
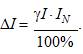
За нормирующее значение IN принимаем размах шкалы, т.к шкала амперметра содержит нулевую отметку
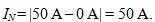
Абсолютная погрешность равна:
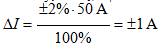
во всех точках шкалы прибора. Заносим данное значение во второй столбец таблицы.
Значения относительной погрешности будем рассчитывать по формуле:
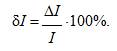
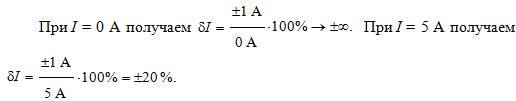
Значения относительной погрешности для остальных измеренных значений тока рассчитываются аналогично.
Полученные таким образом значения относительной погрешности заносим в третий столбец.
По данным табл. 2.1, учитывая, что погрешности могут быть как положительными, так и отрицательными, строим графики зависимостей абсолютной ΔI, относительной δI и приведённой γI погрешностей от результата измерений I (рис. 2.1).
Задачи для самостоятельного решения
Для прибора рассчитать значения абсолютных, относительных и приведённых основных погрешностей измерений. Результаты представить в виде таблицы и графиков.
Таблица 2.2.
Практическое занятие № 2
Дата: 2019-02-19, просмотров: 2801.
