Экспериментальное определение любых свойств материалов сопровождается разбросом получаемых значений. Величина, которая при данных неизменных условиях эксперимента принимает различные значения, называется случайной, а ее конкретные значения – реализациями.
Случайная величина характеризуется областью возможных значений, которые она может принимать в результате опыта, и вероятностью получения этих значений. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина может принимать отдельные изолированные возможные значения из некоторой конечной или бесконечной области (последовательность значений, не заполняющих сплошь никакой интервал).
Большинство свойств материалов и технологических процессов характеризуются непрерывными случайными величинами, возможные значения которых образуют некоторый интервал. Поэтому рассматриваются непрерывные случайные величины.
Для описания случайной величины необходимо знание вероятности принятия ею различных значений. Зависимость между возможными значениями этой величины и соответствующими вероятностями называется законом распределения . Наиболее важной характеристикой случайной величины является интегральная функция F(х), которая называется функцией распределения. Она характеризует вероятность появления значений случайной величины Х, непревосходящих значения х.
F(х) = P(Х £ х).
Графическое изображение функции распределения показано на рис. 1.а. Ясно, что значение функции распределения находится в интервале 0 < F(х) £ 1, а вероятность нахождения случайной величины Х в интервале х Х < х будет
P( х < Х £ х ) = F(х ) - F(х ).
Функция распределения является исчерпывающей характеристикой случайной величины. Однако по ней трудно судить о характере распределения величины в окрестности точек вблизи числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины дает дифференциальная функция, которая называется плотностью распределения вероятностей f(х); при этом
f (х) = F’(х).
Ее графическое изображение представлено на рис. 1.б
Очевидно, что
Вероятность попадания значения случайной величины в ин-тервалах в этом случае будет
Таким образом, знание закона распределения случайной величины в виде функции распределения или плотности распределения позволяет оценивать вероятности попадания их значений в определенный интервал.
Наряду с указанными характеристиками случайных величин существуют числовые характеристики, которые в сжатой форме выражают наиболее существенные особенности распределения; их использование возможно и при неизвестном законе распределения. Основными такими характеристиками являются математическое ожиданиеи десперсия или связанное с ней среднее квадратическое отклонение.
Математическое ожидание непрерывной случайной величины (среднее значение случайной величины) определяется выражением:
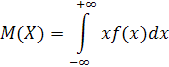
По результатам n реализаций случайной величины x1, x2,…..,xn (вариационный ряд) может быть найдено приблизительное значение математического ожидания, которое является его выборочной оценкой, тем более точной, чем больше число наблюдений
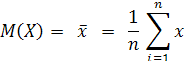
Дисперсия показывает, насколько тесно сгруппированы реализации (рассеяние); это математическое ожидание квадрата отклонения случайной величины с функцией плотности f (x) от ее математического ожидания:
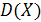 = M(
= M(  .
.
На практике часто пользуются средним квадратическим отклонением
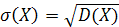 .
.
Напомним некоторые неочевидные свойства математического ожидания и дисперсии:
- постоянный множитель C выносится за знак следующим образом
M(CX) = CM(X),
D(CX) = C2D(X)
- дисперсия суммы и дисперсия разности равна сумме дисперсий
D(X+Y) = D(X) + D(Y),
D(X-Y) = D(X) +D(Y);
- дисперсия среднего квадратичного n независимых случайных величин в n раз меньше дисперсии каждой из величин
D( 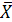 ) =
) =  .
.
Дата: 2019-02-19, просмотров: 355.