Цель занятия:
1.Освоить методику составления, обработки и анализа вариационного ряда.
2. Овладеть способом вычисления средних величин из сгруппированного вариационного ряда.
3. Научиться оценивать достоверность средних величин, определять их доверительные границы и достоверность разности показателей.
Для достижения этой цели студент должен
Знать:
Методику анализа вариационного ряда
Методику оценки достоверности полученных результатов
Уметь:
1. рассчитать среднюю арифметическую простую и взвешенную,
2. дать характеристику разнообразия признака,
3. рассчитать доверительные границы и достоверность разности полученных результатов,
4. дать индивидуальную оценку параметров явления по сигмальному отклонению.
СТРУКТУРА ЗАНЯТИЯ:
1. Контрольный опрос - 10 минут
2. Выполнение учебного задания 5 и обсуждение
результатов - 35 минут
3. Выполнение учебного задания 6 и обсуждение
результатов - 20 минут
4. Объяснение преподавателем закономерностей
распределения частот вариационного ряда и
практического применения сигмальных зон:
-определение крайнего значения вариант
(нормы и патологии)
-индивидуальная оценка параметров явления
по сигмальному отклонению
-для расчета количества продукции с учетом
стандартного распределения частот - 25 минут
5. Выполнение учебного задания 7 и обсуждение результатов - 45 минут
6. Выполнение учебного задания 8 и обсуждение результатов - 40 минут
7. Подведение итога занятия - 5 минут
ЛИТЕРАТУРА
ОСНОВНАЯ:
1. Лекции по социальной гигиене и организации здравоохранения.
2. А.Ф. Серенко, В.В. Ермакова «Социальная гигиена и организация здравоохранения». М., 1984, с. 123-149.
3. Ю.П. Лисицын, Н.Я. Копыт «Руководство к практическим занятиям по социальной гигиене и организации здравоохранения» М., 1984, с.72-94.
4. Ю.П. Лисицын «Руководство по социальной гигиене и организации здравоохранения» М., 1987, с. 22-233.
ДОПОЛНИТЕЛЬНАЯ:
5. Ю.П. Лисицын «Социальная гигиена (медицина) и организация здравоохранения, М., 1998, с. 293-301.
ОСНАЩЕНИЕ ЗАНЯТИЯ
1. Учебный стенд № 2 по статистике: Планшет № 6 «Средние величины»
2. Ситуационные задачи.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Понятие о вариационном ряде. Методика его составления и анализа.
Средняя арифметическая простая. Методика расчета.
Средняя арифметическая взвешенная. Методика ее вычисления
(непосредственным способом и по способу моментов).
Мода и медиана.
Амплитуда и лимит вариационного ряда.
Среднее квадратическое отклонение, коэффициент вариации.
Оценка достоверности результатов исследования.
Ошибка средней арифметической.
Сигмальные зоны, их применение в медицине.
Доверительные границы средних величин.
Оценка достоверности разности между средними величинами.
ИНФОРМАЦИОННОЕ СОДЕРЖАНИЕ ЗАНЯТИЯ
Средняя величина - это величина, которая средним цифровым значением характеризует изучаемое явление или признак.
Виды средних величин:
-мода
-медиана
-средняя арифметическая
-простая
-взвешенная
Недостатки средних величин заключаются в том, что за ними не видно индивидуальных различий изучаемого явления.
Средние величины рассчитываются из вариационного ряда.
Вариационный ряд - ряд чисел, расположенных в определенном порядке, характеризующих один признак, но отличающихся друг от друга по своей величине.
Виды вариационных рядов:
· убывающий
· нарастающий
· неопределенный
· сгруппированный
Вариационный ряд характеризуют следующие признаки: варианта, частота, мода, медиана, амплитуда, лимит, интервал и др.
САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ
УЧЕБНОЕ ЗАДАНИЕ 5
а) Средняя арифметическая простая рассчитывается из вариационного ряда, в котором каждая варианта встречается один раз. Она рассчитывается по формуле:
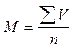
б) Средняя арифметическая взвешенная высчитывается из вариационного ряда, в котором каждая варианта встречается один раз и более.
Она рассчитывается: - непосредственным способом
- по способу моментов
Средняя арифметическая взвешенная непосредственным способом рассчитывается по формуле:
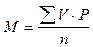
ЗАДАЧА 1. Определите средний вес 25 подростков (непосредственным способом).
| Вес в кг ( V ) | Число подростков ( P ) | VP |
| 59 60 61 62 63 64 65 | 1 4 6 9 3 2 1 |
n = 26
в) Средняя арифметическая взвешенная по способу моментов рассчитывается по формуле:
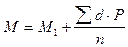
В процессе работы необходимо дать характеристику изучаемого явления (характеристику разнообразия признака). Разнообразие (или похожесть) характеризуют:
- амплитуда
- лимит
- среднеквадратическое отклонение
- коэффициент вариации
г) Среднеквадратическое отклонение (сигма) характеризует колеблемость (вариабельность) вариационного ряда и является его абсолютной мерой. Чем большее число наблюдений будет находиться в пределах + одна сигма от средней арифметической, тем однообразнее будет вариационный ряд.
Сигма для средней арифметической, вычисленной по способу моментов, рассчитывается по формуле:
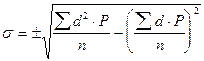
д) Коэффициент вариации характеризует колеблемость (вариабельность) вариационного ряда и является его относительной мерой. Чем меньше показатель, тем однороднее вариационный ряд. Различают степени градации вариации:
низкая (меньше 10,0 %)
средняя (10 - 20,0 %)
высокая ( больше 20,0 %)
е) Кроме характеристики разнообразия признака оценивается достоверность результатов исследования - рассчитываются:
· ошибка средней арифметической
· доверительные границы средней арифметической
· достоверность разности результатов исследования
Ошибка средней арифметической - это поправка к результату выборочного исследования. Величина ошибки (m) показывает на сколько М отличается от результата, который был бы получен при исследовании всей генеральной совокупности. Ошибка рассчитывается по формуле:
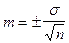
ЗАДАЧА 2. Определите средний рост девушек 12- летнего возраста по способу моментов, среднее квадратическое отклонение, коэффициент вариации и ошибку средней арифметической:
| Рост в см ( V ) | Число девушек ( Р ) | d | dp | d2p |
| 136 137 138 139 140 141 | 15 17 22 20 19 18 |
n = 111
УЧЕБНОЕ ЗАДАНИЕ 6
Произвести группировку вариационного ряда и вычислить среднюю арифметическую по способу моментов.
| Вес подростков в кг ( V ) | Число подростков Р |
| 48,0 48,3 50,7 51,2 52,8 53,0 54,6 55,0 56,4 57,3 58,1 58,5 59,6 60,9 61,2 61,3 61,8 62,4 62,5 63,1 64,9 | 1 3 4 7 11 16 22 27 30 41 39 25 21 20 17 12 9 8 4 2 1 |
n = 20
Группировку провести в следующей последовательности:
1. Определить амплитуду вариационного ряда:
А = Vмакс. - Vмин.
2.Выбрать интервал (классовый промежуток - К)
3.Определить число вариант в сгруппированном интервальном ряду по формуле:
V = 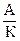 + 1
+ 1
УЧЕБНОЕ ЗАДАНИЕ 7
Доверительные границы средних величин показывают в каких пределах можно доверять результатам выборочного исследования (М), или как он будет колебаться при переносе его на всю генеральную совокупность (М) с определенной долей вероятности (t). Коэффициент вероятности (достоверности) может выражаться в единицах или процентах:
t - 1 = 68,3 %
t - 2 = 95,5 %
t - 3 = 99,7 %
Для большинства медико-биологических исследований достаточной считается вероятность равная 95,5 %.
Доверительные границы рассчитываются по формуле:
М = М + tm
ЗАДАЧА 1. Группа больных коронарным атеросклерозом исследовалась на содержание холестерина в сыворотке крови. Среднее содержание холестерина у всех больных составляло 231+4,0 мг%. Определить доверительные границы средней арифметической с вероятностью безошибочного прогноза Р= 95,5% и Р= 99,7%.
ЗАДАЧА 2. Произведено обследование роста семилетних мальчиков (n=112) города Тобольска. Средний рост составил 123,96 + 0,50 см. Определить доверительные границы средней арифметической с вероятностью безошибочного прогноза Р=95,5%.
УЧЕБНОЕ ЗАДАНИЕ 8
Достоверность разности результатов исследования (t) рассчитывается для определения различия между несколькими показателями. При этом решается вопрос, является ли различие показателей существенным (обусловленным действием каких-то фактов), или вызвано случайными колебаниями.
Достоверность разности рассчитывается по формуле:
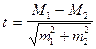
Различия считаются существенными, если t = 2 или больше 2. При этом разность соответствует вероятности безошибочного прогноза равной 95,5 %.
ЗАДАЧА 1. Изучалась обсемененность кожных покровов патогенной и условно-патогенной флорой с одновременным анализом других иммунологических показателей у онкологических больных по сравнению с группой здоровых.
| Число Обследованных (n) | Среднее число микробных клеток на коже предплечья (М) | M | T | |
| Больные ра- ком яичников Здоровые женщины | 28 20 | 78,5 29,7 | + 3,0 + 2,0 |
Определить существенны ли различия показателей обсемененности кожных покровов патогенной и условнопатогенной флорой в сравниваемых группах женщин.
ЗАДАЧА 2. Студентов-медиков исследовалось артериальное давление до и после сдачи экзаменов. Максимальное артериальное давление до сдачи экзаменов в среднем составило 127,2 + 3,0. После сдачи - 117,0 + 4,0 мм.рт.ст. Можно ли на основании этих данных считать, что действительно до сдачи экзаменов у студентов отмечалось некоторое повышение максимального артериального давления?
ТЕСТОВЫЕ ЗАДАНИЯ
Дата: 2019-02-19, просмотров: 640.