С адиабатическим подъемом влажного ненасыщенного воздуха связано такое важное изменение, как приближение его к состоянию насыщения. Температура воздуха при его подъеме понижается; поэтому на какой-то высоте достигается насыще­ние. Эта высота называется уровнем конденсации.

При дальнейшем подъеме влажный насыщенный воздух охлаждается иначе, чем ненасыщенный. В нем происходит кон­денсация, а при конденсации выделяется в значительных коли­чествах скрытая теплота парообразования, или теплота конден­сации. Выделение этой теплоты замедляет понижение темпера­туры воздуха при подъеме. Поэтому в поднимающемся насы­щенном воздухе температура падает уже не по уравнению Пу­ассона, а по влажноадиабатическому закону. Она падает тем медленнее, чем больше влагосодержание воздуха в состоянии насыщения (что в свою очередь зависит от температуры и дав­ления).

Падение температуры в насыщенном воздухе при подъеме его на единицу высоты (100 м) называют влажноадиабатическим градиентом Г _s .

При очень низких температурах, которые получает воздух при подъеме в высокие слои атмосферы, водяного пара в нем остается немного и выделение теплоты конденсации поэтому также мало. Падение температуры при подъеме в таком воз­духе приближается к падению в сухом воздухе. Иначе говоря, влажноадиабатический градиент при низких  температурах при­ближается по величине к сухоадиабатическому.

При опускании насыщенного воздуха процесс может про­исходить по-разному в зависимости от того, содержит ли воз­дух жидкие продукты конденсации (капельки и кристаллы), или они уже целиком выпали из воздуха в виде осадков.

Если в воздухе нет продуктов конденсации, то воздух, как только температура в нем начнет при опускании расти, сразу станет ненасыщенным. Поэтому воздух, опускаясь, будет нагре­ваться по сухоадиабатическому закону, т. е. на 1°/100 м. Если же в воздухе есть капельки и кристаллы, то они при опускании и нагревании воздуха будут постепенно испаряться. При этом часть тепла воздушной массы перейдет в скрытую теплоту па­рообразования, и потому повышение температуры при опуска­нии замедлится. В результате воздух останется насыщенным до тех пор, пока все продукты конденсации не перейдут в газооб­разное состояние. А температура в нем будет в это время повы­шаться по влажноадиабатическому закону: не на 1°/100 м, а на меньшую величину — именно на такую, на какую понизилась бы температура в восходящем насыщенном воздухе при тех же значениях температуры и давления.

Псевдоадиабатический процесс

Представим себе, что влажный ненасыщенный воздух сначала поднимается. Его температура при этом падает сначала по су­хоадиабатическому закону; затем, после того как достигнут уровень конденсации, — по влажноадиабатическому закону.

До­пустим также, что вся вода, выделяющаяся при конденсации, сразу же выпадает из воздуха в виде осадков. Допустим затем, что, достигнув некоторой высоты, воздух начинает опускаться. Так как продуктов конденсации в нем нет, то он будет при этом нагреваться по сухоадиабатическому закону. Легко рассчитать, что на прежний уровень воздух придет с температурой более высокой, чем та, которая была в нем первоначально.

Рассматриваемая масса воздуха совершила необратимый процесс. Хотя она вернулась на прежний уровень, под прежнее давление, она не вернулась в исходное состояние: ее конечная температура оказалась выше, чем была начальная. Такой про­цесс называется псевдоадиабатическим.

Адиабатная диаграмма

Построим график для изменения температуры при адиабатическом процессе в вертикально движущемся воздухе, откладывая по оси абсцисс температуру, а по оси ординат высоту. Кривая, графически представляющая это изменение температуры, называется адиабатой.

Выше мы нашли, что при сухоадиабатическом процессе изменение температуры на единицу изменения высоты есть величина постоянная, равная почти точно 1°/100 м. Поэтому если температура и высота отложены по осям в линейной шкале, то сухие адиабаты должны представляться прямыми линиями. Но изменение температуры при влажноадиабатическом процессе есть величина переменная. Поэтому кривые, представляющие влажноадиабатическое изменение в осях координат темпера­тура — высота, влажные адиабаты, являются именно кривыми, а не прямыми линиями. Они наклонены к оси абсцисс меньше, чем сухие адиабаты. Но в высоких слоях, где влажноадиабатический градиент приближается по величине к сухоадиабатическому, наклон влажных адиабат приближается к наклону сухих адиабат. Поэтому на графике влажные адиабаты будут иметь выпуклость вверх (рис. 5).

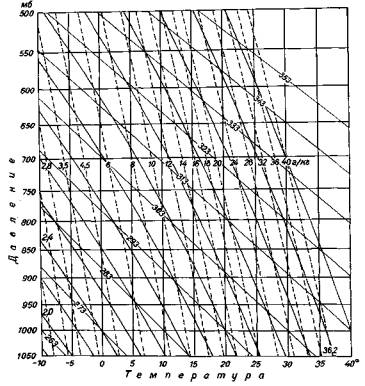
Рис. 5. Адиабатная диаграмма (сплошные линии с большим углом наклона — сухие адиабаты, с меньшим углом наклона — влажные адиабаты, прерывистые линии — изолинии удельной влажности для состояния насыщения).

Аналогичным образом можно построить адиабаты в осях координат температура — давление, поскольку температура при адиабатических процессах меняется в зависимости от изменения давления.

Адиабатной диаграммой называют график, на который нанесены семейства сухих и влажных адиабат для различных значений температуры и высоты (или давления).

С помощью адиабатной диаграммы можно графически определить изменение состояния при адиабатических процессах. Например, зная температуру Т₀ и давление р₀ в начальный момент, найдем на диаграмме соответствующую точку. Если затем воздух меняет свое состояние по сухоадиабатическому закону, пока не достигнет давления р, следуем по сухой адиабате, проходящей через начальную точку, до тех пор, пока она (адиабата) не пересечется с ординатой р. Тогда сразу же определим по диаграмме, каково будет значение температуры воздуха при давлении р. Если при каком-то давлении р воздух стал насыщенным, нужно дальше прослеживать его состояние по влажной адиабате, проходящей через точку, соответствующую давлению р.

Потенциальная температура

Пусть на какой-то высоте в атмосфере имеется воздух с давлением р и температурой Т. Если бы этот воздух сухоадиабатически опустился на уровень, где существует стандартное давление р₀, то температура его тоже изменилась бы по уравне­нию Пуассона. Новая температура была бы

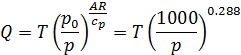
Назовем эту температуру, которую воздух получил бы при стандартном давлении (1000 мб), его потенциальной темпера­турой. Фактическую температуру воздуха, в отличие от потен­циальной, будем называть молекулярной температурой. Оче­видно, что потенциальная температура равна молекулярной тем­пературе при стандартном давлении.

Потенциальную температуру можно с достаточным прибли­жением определить, если известно, на какой высоте воздух на­ходится. Пусть, например, эта высота равна 3000 м . Допустим, что на уровне моря давление стандартное, т. е. равно 1000 мб (в среднем оно близко к этой величине). Тогда потенциальная температура воздуха, т. е. температура, с которой он пришел бы на уровень моря, равна его начальной температуре плюс 30°, так как на каждые 100 м спуска температура воздуха должна возрастать на один градус.

Таким образом, приближенно

Θ = T + z , где z — число градусов, равное числу гектометров вы­соты.

С помощью потенциальной температуры можно сравнивать тепловое состояние масс воздуха, находящихся на разных вы­сотах над уровнем моря, т. е. при разных давлениях. Вычисляя потенциальную температуру этих масс, мы как бы опускаем их на один уровень.